Table of Contents |
Unlike the cash payback method and the average rate of return, the capital budgeting selection method in this lesson takes into account the time value of money in its analysis. Net present value is a project valuation method that compares the initial investment amount of a project to the present value of future cash flows. This often more complex method can give decision makers even keener insight into proposed capital projects and what types of returns they bring.
To simplify our calculations, we will assume that all net cash inflows occur at the end of the year. Often used in capital budgeting analysis, this assumption makes the calculation of present values less complicated than if we assume the cash flows occurred at various times throughout the year.
In order to understand the following methods of capital project selection, we must first learn how money behaves, namely understanding present value concepts.
In the previous tutorial, Capital budgeting, you learned that the time value of money is the principle that a sum of money that you have now is more valuable than that same sum of money in the future. This concept takes into account that a predicted value of cash inflow (sometime in the future) is not equivalent to the same amount received at an earlier date. This idea is the key element of understanding present value.
Present value is the current value of a future sum of money, given a specified rate of return. The present value concept recognizes the time value of money, which says that a current sum of money can be invested at a given interest rate to produce a future return.
To illustrate present value, consider the scenario of receiving $1,000 today or $1,000 in five years. Because these two values would be received in two different time periods, they cannot be truly compared until they have been converted to today’s value, known as present value.
Present value is calculated by dividing the future value of an amount of money by one plus the interest rate raised to the number of periods of interest received power. This process is also commonly known as discounting.
EXAMPLE
Calling back to our example of receiving $1,000 today or receiving $1,000 in five years, and assuming we can earn a rate of return on investing money of 10%, we can calculate the present value of the $1,000 we would receive in five years by using the present value formula.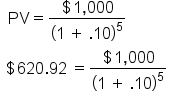
You may be wondering how the 10% rate of return in the example was determined. Rate of return is the amount a business expects to earn if they invest money. Rate of return can be determined in several ways:
Now that we understand how to calculate the present value (discount) of a singular cash amount, we need to learn how to calculate the present value of a series of cash flows, called an annuity. An annuity is a series of equal net cash flows for consecutive periods. Annuities, for our purpose in capital budgeting, are the cash inflows that a capital investment pays per period. There are three different ways we can calculate the present value of an annuity.
EXAMPLE
On January 1, City Signs, an outdoor political signage company, plans to invest in a machine that will produce $5,000 of cash inflow for each of the next five years. The current market interest rate is 12%. In the following sections, we will look at three different ways to calculate the present value of annuities for City Signs.The first way to calculate an annuity's present value is to use the present value formula five separate times to discount each yearly cash flow. All of the present values are then added to determine the total present value for the five cash flows.
EXAMPLE
To use the present value formula method for calculating City Signs' investment annuity, calculate the present value for each of the next five years and add them all together.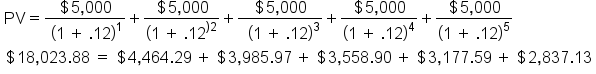
Present value annuity tables are based on the present value formula and enable the user to simply multiply an annuity (equal amounts per period) by a present value factor to determine the present value. The user cross references the interest factor by the number of periods.
EXAMPLE
City Signs can earn a 12% rate of return for 5 periods. Using the annuity table we find the present value factor is 3.6048 for this rate and number of periods. The present value factor is multiplied by the amount of the annuity to determine the total present value of the capital project.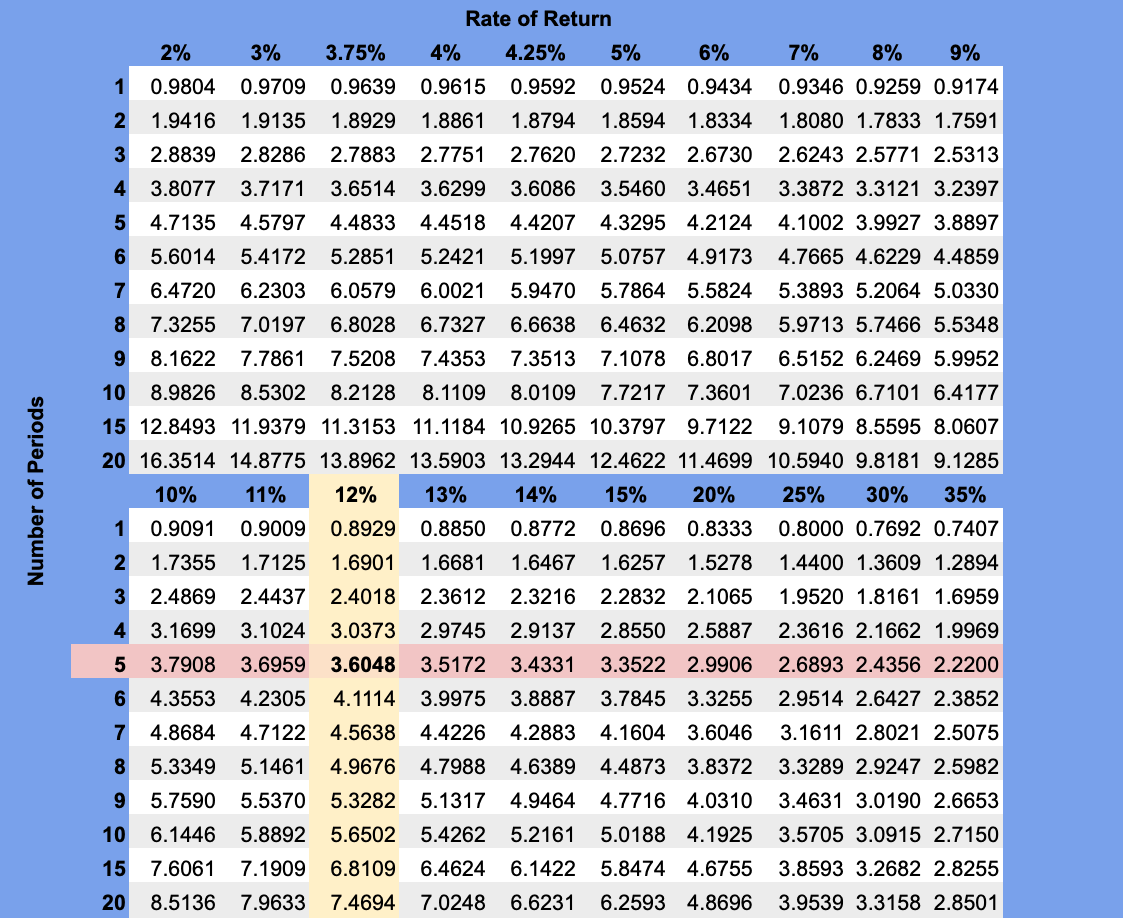
The third way the present value of an annuity can be determined is by using technology, like an online annuity calculator or a spreadsheet application. The following figure was developed in Google Sheets using the pv function.
EXAMPLE
Businesses that make capital investment decisions need to understand the full financial impact of those decisions. Before capital expenditures can be approved, decision makers must weigh potential earnings against the risks for each investment. One way to accomplish this is by using the net present value method.
The net present value method compares the initial investment amount of a project to the present value of future cash flows and should be used when a business wants to discount future cash flows to determine if a capital project will be profitable in the long run. For this reason, net present value is often referred to as the discounted cash flow method. Using what we learned earlier in this lesson about present value calculations, all future cash flows will be discounted to calculate the net present value of the investment. Then, this net present value is compared to the initial investment amount to determine whether the capital expenditure should be funded. If the net present value of the investment is greater than the amount to be invested, then the company should move forward with the project.
EXAMPLE
To illustrate, assume TB Corporation desires to replace its computer equipment for its entire business. TB has amassed the following data concerning this proposed capital project:| Cost of New Equipment | $100,000 |
| Expected Useful Life | 5 years |
| Minimum desired rate of return | 15.00% |
| Expected Cash Flows: | |
| Year 1 | $35,000 |
| Year 2 | 30,000 |
| Year 3 | 25,000 |
| Year 4 | 20,000 |
| Year 5 | $20,000 |
Since there are different cash inflows per period, each cash inflow will need to be calculated separately. Remember you can use the present value equation, a present value table, or technology to determine the present value. In this example, we will use the present value equation.
EXAMPLE
Next, we find the total present value by adding together the present value of each future period.
EXAMPLE
Adding together the five present value figures from step one ($30,434.78 + $22,684.31 + $16,437.91+ $11,435.06 + $9,943.53) yields a total present value of $90,935.60.Calculate the net present value by subtracting the initial cost of the investment from the total present value of future cash inflows. This value tells you whether the project will make or lose money.
EXAMPLE
| Total Present Value of Future Cash Inflows | Initial Cost of Investment |
| $90,935.60 | $100,000 |
At this point, management has only a simple decision to make based on whether the total present value shows that the investment will meet the minimum desired rate of return. This is the net present value decision rule.
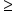the initial cost of the investment, then the project meets the minimum desired rate of return and should be funded. (Net present value is 0 or positive)EXAMPLE
The net present value of future cash inflows of the computer equipment is less than the amount to be invested (negative $9,064.40), therefore the project does not meet the 15% desired rate of return standard and should not be funded.Like cash payback and internal rate of return, using net present value presents its own set of advantages and disadvantages.
| Advantages of the net present value method | Disadvantages of the net present value method |
|---|---|
|
|
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM “ACCOUNTING PRINCIPLES: A BUSINESS PERSPECTIVE” BY hermanson, edwards, and maher. ACCESS FOR FREE AT www.solr.bccampus.ca. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNPORTED.
Net Present Value = Total Present Value of Future Cash Inflows - Amount to be Invested
Present Value = Annuity Amount Per Period x Present Value Factor
Present Value of the Annuity = PV1 + PV2 + PV3 + PV4 + PV5
Total Present Value of Future Cash Inflows = PV1 + PV2 + PV3 + PV4 + PV5
