Earlier, we were using the equation of a rational function to determine all its characteristics. Because of the relationship between the equation and these characteristics, we can also write a possible equation of a rational function if we know its characteristics.
EXAMPLE
Write an equation of the rational function whose graph is shown here.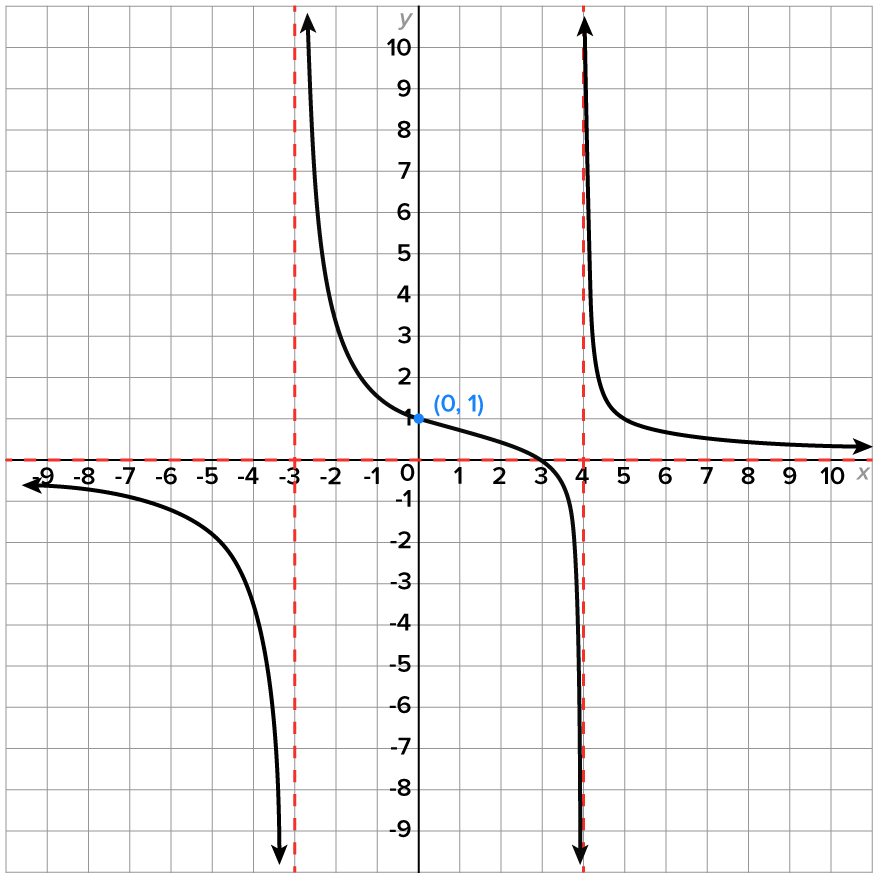
This suggests that the degree of the numerator is smaller than the degree of the denominator. 
and 
and 
which means that the denominator contains 
and 
as factors. Upon further inspection, the behavior of the graph around the asymptotes suggests that each has odd multiplicity (
on one side of the asymptote and 
on the other side). Thus, the factored form of the denominator is 
which means that 
is a factor of the numerator.
where 
is a stretch factor that isn’t apparent from the graph. Similar to our work with polynomials, we use another point on the graph to determine what the value of is. In this case, we use the y-intercept.
we know 
By our equation, 
which means 
which is also written 
Now that we have worked through one example, here are some steps to follow when building an equation of a rational function.
Now, let’s look at a more involved example.
EXAMPLE
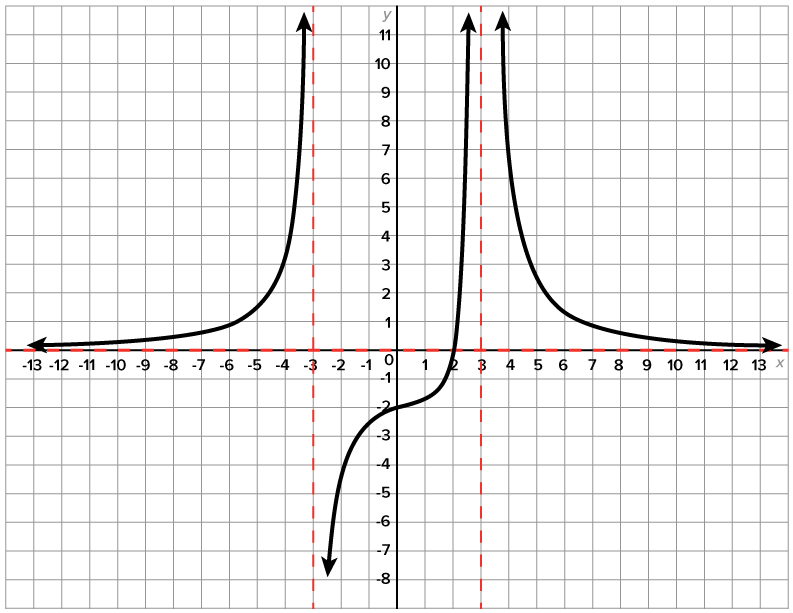
Write an equation of the rational function whose graph is shown below.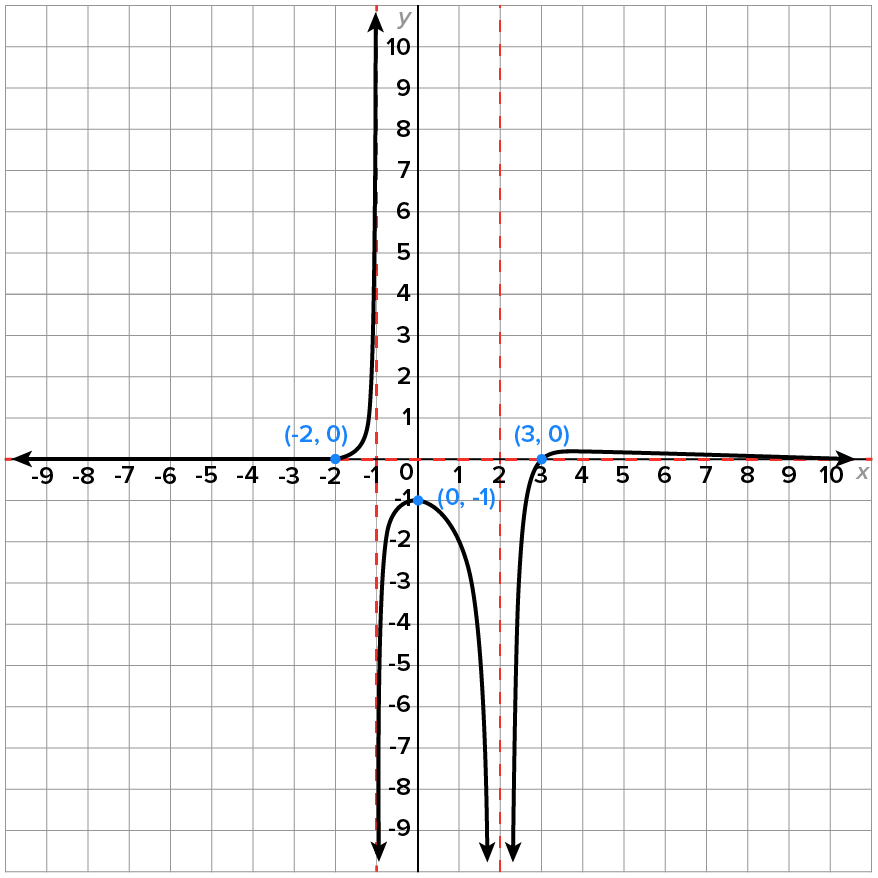
This suggests that the degree of the numerator is smaller than the degree of the denominator. 
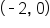and 
and
and 
which means that the denominator contains 
and 
as factors.
suggests odd multiplicity since on one side and on the other side.
suggests even multiplicity since on both sides of Therefore, the factored form of the denominator is 
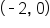and which means that 
and are factors of the numerator. Since the graph crosses the x-axis at each intercept, each factor has odd multiplicity, so we will assume that each is linear (multiplicity 1). Then, the numerator is 
where is a stretch factor that isn’t apparent from the graph. Similar to our work with polynomials, we use another point on the graph to determine what the value of is. In this case, we use the y-intercept.
we know 
By our equation, 
which means 
which is also written 
Here is one more worked-out example that involves an oblique asymptote.
EXAMPLE
Write an equation of the rational function whose graph is shown here.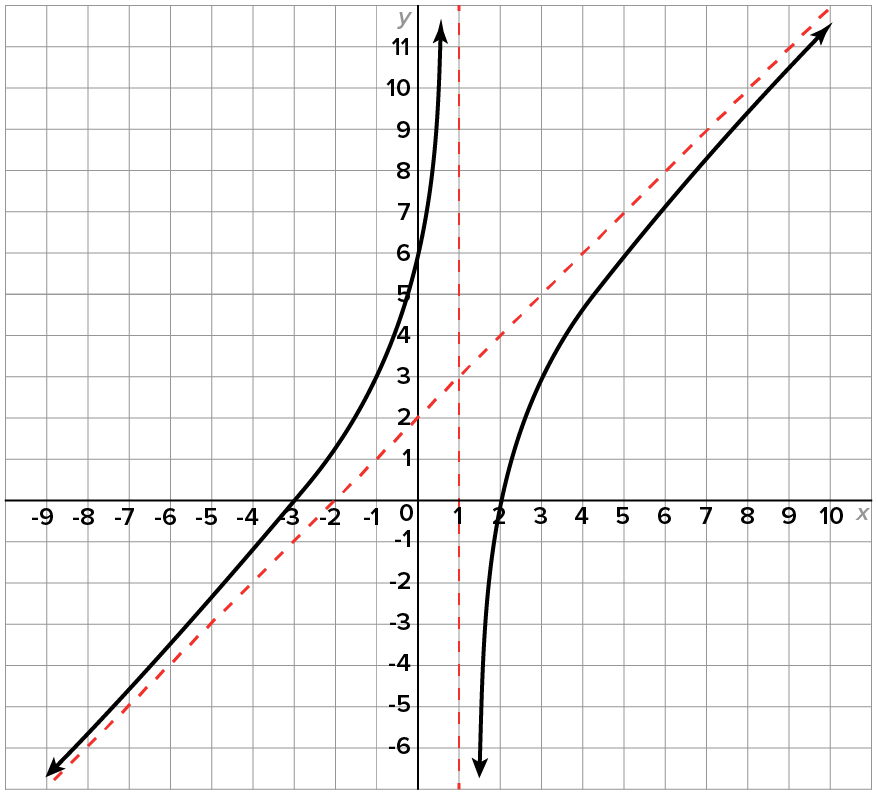
and 
on one side of the vertical asymptote and on the other side, 
has odd multiplicity. This means that the denominator is 
corresponds to 
and 
corresponds to 
the factored form of the numerator is 
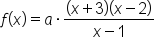for some stretch factor 
we know 
which means 
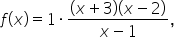or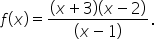 
Well, hello. In this video, we're going to look at how to write the equation of a rational function whose graph is given. Now when we look at this graph, one of the first things we want to note is that there is a hole in the graph at the point negative 1, comma 4. So with that hole in the graph at negative 1, comma 4, I know that x minus negative 1 or x plus 1 is a common factor of both the numerator and the denominator.
So we are going to start by giving structure to what we're going to fill in, and then, with that hole in the graph, realize, that we have that common factor of x plus 1 in the numerator in the denominator because of the hole in the graph.
Next up, we see that there is a vertical asymptote at x equal 1. And if there's a vertical asymptote for the graph, I know that x minus that value-- so x minus 1-- is a factor in the denominator, but not in the numerator.
One thing that we want to realize is when we're writing this equation of a rational function, we want to write it where we have the smallest degree possible of the numerator and denominator. And so while there are a lot of other ones that you can write, we want to write the one with the lowest degrees.
Next up, we see that there is an x-intercept at x equal 3, comma 0. So that means that there is a factor of x minus 3 in the numerator of the function.
Now that we have that part of the function set up from all of that information, we need to find our value of a, which is the stretch of the graph. And we can do that by finding a point on the function that lends us to having an easy way of finding it. And that is using our y-intercept.
So the y-intercept on this graph is 0, comma 6. So that means when 0 goes in for the function, 6 comes out. Now if we take f of 0 in our structured form, that's a times 0 plus 1 times 0 minus 3 over 0 plus 1 times 0 minus 1. And so that gives us that f of 0 is equal to 3a.
But I also know that I have the y-intercept of 0, comma 6. So if 0 goes into the function, 6 is my output. So that means, then, that 3a has to be the same as 6.
Solving for a, I get a is equal to 2. And then that gives me my final form of my function, f of x is equal to-- well, one step shy of final form of my function. It's 2 times the x plus 1 times x minus 3 over x plus 1 times x minus 1, which we can write with our 2 in the numerator.
And multiplied out and distribute the 2 through the numerator-- we have 2x squared minus 4x minus 6, all over x squared minus 1. And that is the equation of the function that has the given graph.
Earlier, we discussed real-life situations that were modeled by rational functions. Since we know so many more characteristics of rational functions now, they can be interpreted with real-life meaning.
EXAMPLE
Suppose you have a saltwater solution that contains 5 pounds of salt dissolved in 50 gallons of water. A tap is turned on that adds 4 gallons of water to the solution each minute, and at the same time, 0.5 pounds of salt is added each minute.
where t is the number of minutes since the water was turned on.
|
|
Set the denominator equal to 0. |
|
|
Solve for t. |
The concentration of acid in the solution approaches 80%.SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS
