Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Writing Equations of Exponential Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will write equations of exponential functions using information, which could include a verbal description or two points that are known. Specifically, this lesson will cover:

Table of Contents

1. Writing Equations Using Percent Increase and Decrease

The goal of this challenge will be to write exponential functions in the form 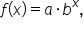f open parentheses x close parentheses equals a times b to the power of x comma where a is a nonzero number and b is a positive number not equal to 1.

Earlier, you may recall, we saw situations in which a constant percent increase or decrease can be modeled by an exponential function.

EXAMPLE

Suppose the value of a house is predicted to increase by 3.4% per year for the foreseeable future. If its value now is $280,000, then what is an exponential model for the value of the home x years from now?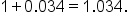

The decimal version of the percent increase is 0.034. This means that the factor by which the value of the home increases from year to year is 1 plus 0.034 equals 1.034.

To calculate the value of the home after x years, start at 280000, then multiply 1.034 for each year after the starting point.

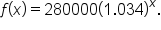
Since the starting value of the home is 280000, the function that describes the value of the home after x years is f open parentheses x close parentheses equals 280000 open parentheses 1.034 close parentheses to the power of x.

Here is another example where a quantity is decreasing over time.

EXAMPLE

After taking 100 milligrams of medicine, the quantity of medicine in one’s bloodstream decreases by 30% every hour. What is the exponential function that models the amount of medicine remaining in the bloodstream after t hours?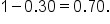

The decimal version of the percent decrease is 0.30. This means that the factor by which the amount of medicine in the bloodstream changes from one hour to the next is 1 minus 0.30 equals 0.70.

To calculate the amount of medicine in the bloodstream after t hours, start at 100 mg, then multiply 0.70 for each hour after the starting point.

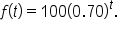
Since there is initially 100 milligrams of medicine in the bloodstream, the function that describes the amount of medicine in the bloodstream after t hours is f open parentheses t close parentheses equals 100 open parentheses 0.70 close parentheses to the power of t.

big idea
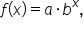Given an exponential model of the form f open parentheses x close parentheses equals a times b to the power of x comma considering for now a greater than 0 comma we observe these behaviors:
  • When b greater than 1 comma the value of f open parentheses x close parentheses increases as x increases.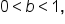
  • When 0 less than b less than 1 comma the value of f open parentheses x close parentheses decreases as x increases.
When we talk about graphs of exponential functions later in this challenge, we will discuss the behavior of f open parentheses x close parentheses when a less than 0.

try it
The starting salary for an engineer at a large company is $70,000 for one year, with a 5.2% raise in salary per year.
Write an exponential function for the annual salary t years after starting.
Since the salary increases by 5.2% each year, the salary grows exponentially with the growth factor 1 plus 0.052 equals 1.052.

In addition, the starting salary is $70,000, which means that the salary is described by the model f open parentheses t close parentheses equals 70000 open parentheses 1.052 close parentheses to the power of t.

2. Writing Equations Given Two Solution Points

When the growth (or decay) rate is unknown, we need to find a and b in the equation 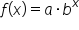f open parentheses x close parentheses equals a times b to the power of x some other way. Since there are two values to find, we can use two solution points to write the equation.

EXAMPLE

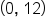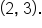
Write the equation of an exponential function f open parentheses x close parentheses that contains solution points open parentheses 0 comma space 12 close parentheses and open parentheses 2 comma space 3 close parentheses.

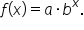
Start with f open parentheses x close parentheses equals a times b to the power of x.

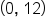Since open parentheses 0 comma space 12 close parentheses is a solution point, this means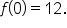 f open parentheses 0 close parentheses equals 12.

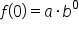
f open parentheses 0 close parentheses equals a times b to the power of 0 Replace 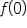x with 0.
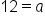
12 equals a open parentheses 1 close parentheses Replace f open parentheses 0 close parentheses with 12, and simplify b to the power of 0 equals 1.
12 equals a Solve for 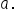a.

Since open parentheses 2 comma space 3 close parentheses is a solution point, this means 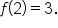f open parentheses 2 close parentheses equals 3.

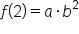
f open parentheses 2 close parentheses equals a times b squared Replace x with 2.
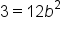
3 equals 12 b squared Replace 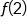f open parentheses 2 close parentheses with 3 and a with 12.
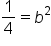
1 fourth equals b squared Divide both sides by 12 and simplify.
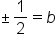
plus-or-minus 1 half equals b Apply the square root principle.
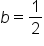
b equals 1 half The value of b must be positive according to the definition of an exponential function. Therefore, 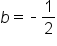b equals short dash 1 half is not considered.

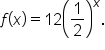
Now, the equation of the exponential function is f open parentheses x close parentheses equals 12 open parentheses 1 half close parentheses to the power of x.

try it
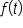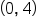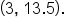
An exponential function f open parentheses t close parentheses has solution points open parentheses 0 comma space 4 close parentheses and open parentheses 3 comma space 13.5 close parentheses.
Write the equation for f   (t  ).
Start with the equation f open parentheses t close parentheses equals a times b to the power of t.

Since open parentheses 0 comma space 4 close parentheses is a solution point, this means a equals 4.

Now, update the equation: f open parentheses t close parentheses equals 4 times b to the power of t.

Next, using the point open parentheses 3 comma space 13.5 close parentheses comma we know that f open parentheses 3 close parentheses equals 13.5.

f open parentheses 3 close parentheses equals 4 times b cubed Replace t with 3 in the equation f open parentheses t close parentheses equals 4 times b to the power of t.
13.5 equals 4 b cubed Replace f open parentheses 3 close parentheses with 13.5.
3.375 equals b cubed Divide both sides by 4.
b equals 1.5 Take the cube root of both sides.

Thus, b equals 1.5 comma and the equation for the exponential model is f open parentheses t close parentheses equals 4 open parentheses 1.5 close parentheses to the power of t.

Notice how the previous problems were very nice to solve since the point 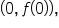open parentheses 0 comma space f open parentheses 0 close parentheses close parentheses comma the y-intercept, was known. When the y-intercept is not known, more advanced algebraic techniques are required.

EXAMPLE

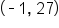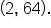
Determine the equation of an exponential function that contains solution points open parentheses short dash 1 comma space 27 close parentheses and open parentheses 2 comma space 64 close parentheses.

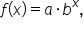Using the equation f open parentheses x close parentheses equals a times b to the power of x comma substitute each solution pair in order to find a and b.

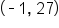Since open parentheses short dash 1 comma space 27 close parentheses is a solution point, it follows that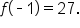 f open parentheses short dash 1 close parentheses equals 27.

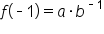
f open parentheses short dash 1 close parentheses equals a times b to the power of short dash 1 end exponent Replace x with -1.
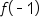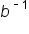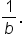
27 equals a times 1 over b Replace f open parentheses short dash 1 close parentheses with 27, and rewrite b to the power of short dash 1 end exponent as 1 over b.
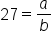
27 equals a over b Rewrite the right-hand side as one fraction.

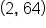Since open parentheses 2 comma space 64 close parentheses is a solution point, it follows that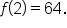 f open parentheses 2 close parentheses equals 64.

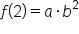
f open parentheses 2 close parentheses equals a times b squared Replace x with 2.
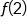64 equals a b squared Replace f open parentheses 2 close parentheses with 64.

At this point, we have two equations in the unknowns a and b. These are not linear equations as we are accustomed to, but we can still solve using the substitution method.

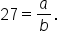Consider the equation 27 equals a over b. Multiplying both sides by b gives 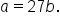a equals 27 b. This can now be substituted into the other equation, which can then be solved for b.

64 equals a b squared Start with this equation.
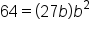
64 equals open parentheses 27 b close parentheses b squared Substitute 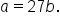a equals 27 b.
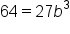
64 equals 27 b cubed Simplify the right-hand side.
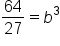
64 over 27 equals b cubed Divide both sides by 27.
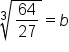
cube root of 64 over 27 end root equals b Take the cube root of both sides.
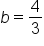
b equals 4 over 3 Simplify.

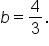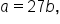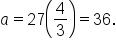
Thus, b equals 4 over 3. Substituting into the equation a equals 27 b comma we find a equals 27 open parentheses 4 over 3 close parentheses equals 36.

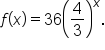
Therefore, the equation of the exponential function is f open parentheses x close parentheses equals 36 open parentheses 4 over 3 close parentheses to the power of x.

watch
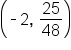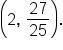
Check out this video that demonstrates how to write the equation of the exponential function that passes through open parentheses short dash 2 comma space 25 over 48 close parentheses and open parentheses 2 comma space 27 over 25 close parentheses.

try it
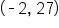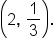
Consider an exponential function that contains solution points open parentheses short dash 2 comma space 27 close parentheses and open parentheses 2 comma space 1 third close parentheses.
Write the equation of the exponential function.
The equation of the exponential model is f open parentheses x close parentheses equals a times b to the power of x. To find a and b, substitute the given points into the equation, then solve.

Using the point open parentheses short dash 2 comma space 27 close parentheses comma we have:

f open parentheses short dash 2 close parentheses equals a times b to the power of short dash 2 end exponent Replace x with -2 in the equation.
27 equals a times b to the power of short dash 2 end exponent Replace f open parentheses short dash 2 close parentheses with 27.
27 equals a over b squared Rewrite the right-hand side using positive exponents.

Now, using the point open parentheses 2 comma space 1 third close parentheses comma we have:

f open parentheses 2 close parentheses equals a times b squared Replace x with 2 in the equation.
1 third equals a b squared Replace f open parentheses 2 close parentheses with 1 third.

Now, we have two equations in two unknowns. Using the first equation, we can multiply both sides by b squared to get a equals 27 b squared.

Now, substitute this into the second equation and solve:

1 third equals a b squared This is the second equation.
1 third equals open parentheses 27 b squared close parentheses b squared Substitute a equals 27 b squared.
1 third equals 27 b to the power of 4 Simplify the right-hand side.
1 over 27 times 1 third equals b to the power of 4 Multiply both sides by 1 over 27.
1 over 81 equals b to the power of 4 Simplify the left-hand side.
plus-or-minus 1 third equals b Take the 4th root of both sides, remembering that there is technically a positive and negative solution.

Since a requirement for an exponential model is that b greater than 0 comma we use b equals 1 third.

Next, find a.

Using the equation a equals 27 b squared comma we have a equals 27 open parentheses 1 third close parentheses squared equals 27 open parentheses 1 over 9 close parentheses equals 3.

Thus, the equation of the exponential model is f open parentheses x close parentheses equals 3 open parentheses 1 third close parentheses to the power of x.

summary
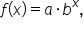In this lesson, you learned how to write the equation of an exponential function in the form f open parentheses x close parentheses equals a times b to the power of x comma where a is a nonzero number and b is a positive number not equal to 1, using two different methods: If known, you can use the starting value and corresponding percent increase and decrease, or you can write the equation given two solution points. It is important to note that when solving for the base b, remember that b has to be positive.

SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.