Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Writing an Equation from a Graph

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to identify an equation in slope-intercept form that corresponds to a given graph. Specifically, this lesson covers:

Table of Contents

1. Review of Slope and Intercepts

Before we begin to write equations from a graph, let's review some important information about the graphs of lines: slopes and intercepts. Being able to easily identify slopes and intercepts from a graph will be extremely useful when writing the equation to the line.

The slope of a line can be found by using any two points on a graph. All we need are the x- and y-coordinates from two points to plug into our equation for slope:

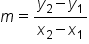
m equals fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction

Intercepts are where the line crosses a particular axis. The y-intercept is the location where the line crosses the y-axis, and it has coordinates of 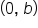left parenthesis 0 comma space b right parenthesis.

2. Determining the Slope-Intercept Form from a Graph

Now that we know how to draw a graph from the slope-intercept form, we can do this in reverse and determine the slope-intercept form from a drawn graph. Again, this skill requires initiative to apply a skill you know in a different manner.

step by step
  1. Determine your y-intercept.
  2. Determine your slope.
  3. Write the equation.

EXAMPLE

Write the equation of the line for the graph below in slope-intercept form.

A graph with an x-axis and a y-axis, both ranging from −6 to 6. A line slants upward from left to right, passing through the two marked points (0,-5) and (1,3) and covering the third, fourth, and first quadrants.

  1. Determine your y-intercept. We can determine where the y-intercept is. Starting at (0, 0), we can count down in the negative direction and see that the y-intercept is (0, -5). We now have our b value.

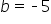
    b equals short dash 5

  2. Determine your slope. You can choose any two points of a line to determine the slope. Just make sure the line actually passes through that coordinate point. Let’s use the two coordinate points identified and determine our slope: (0, -5) and (1, 3).

    m equals fraction numerator 3 minus open parentheses short dash 5 close parentheses over denominator 1 minus 0 end fraction equals 8 over 1 equals 8

  3. Write the equation. Now that we know the y-intercept and slope, we can substitute these values into our formula:

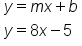
    table attributes columnalign left end attributes row cell y equals m x plus b end cell row cell y equals 8 x minus 5 end cell end table

EXAMPLE

Determine the equation of the line in slope-intercept form based on the graph below:

: A graph with an x-axis and a y-axis, both ranging from −6 to 6. A line slants downward from left to right, passing through the two marked points (0,4) and (3,0) and covering the second, first, and fourth quadrants.

  1. Determine your y-intercept. We can determine where the y-intercept is. By counting up in the positive direction, we can see that the y-intercept is 4. We now have our b value.

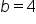
    b equals 4

  2. Determine your slope. Let’s use the two coordinate points identified and determine our slope: (0, 4) and (3, 0).

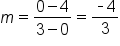
    m equals fraction numerator 0 minus 4 over denominator 3 minus 0 end fraction equals fraction numerator short dash 4 over denominator 3 end fraction

  3. Write the equation. Now that we know the y-intercept and slope, we can substitute these values into our formula:

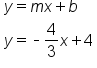
    table attributes columnalign left end attributes row cell y equals m x plus b end cell row cell y equals short dash 4 over 3 x plus 4 end cell end table

EXAMPLE

Determine the equation of the line in slope-intercept form based on the graph below.

A graph with an x-axis and a y-axis, both ranging from −6 to 6. A line slants upward from left to right, passing through the two marked points (0,−5) and (4,5) and covering the third, fourth, and first quadrants.

  1. Determine your y-intercept. We can determine where the y-intercept is. By counting down in the negative direction, we can see that the y-intercept is -5. We now have our b value.

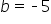
    b equals short dash 5

  2. Determine your slope. Let’s use the two coordinate points identified and determine our slope: (0, -5) and (4, 5).

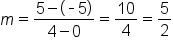
    m equals fraction numerator 5 minus open parentheses short dash 5 close parentheses over denominator 4 minus 0 end fraction equals 10 over 4 equals 5 over 2

  3. Write the equation. Now that we know the y-intercept and slope, we can substitute these values into our formula:

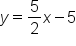
    y equals 5 over 2 x minus 5

try it
Consider the following graph:

A graph with an x-axis and a y-axis, both ranging from −6 to 6. A line slants downward from left to right, passing through the two marked points (0,2) and (6,1) and covering the second and first quadrants.

What is the equation of the line in slope-intercept form?
  1. Determine your y-intercept. We can determine where the y-intercept is. By counting up in the positive direction, we can see that the y-intercept is 2. We now have our b value.

    b equals 2

  2. Determine your slope. Let’s use the two coordinate points identified and determine our slope: (6, 1) and (0, 2).

    m equals fraction numerator 2 minus 1 over denominator 0 minus 6 end fraction equals fraction numerator 1 over denominator short dash 6 end fraction

  3. Write the equation. Now that we know the y-intercept and slope, we can substitute these values into our formula:

    table attributes columnalign left end attributes row cell y equals m x plus b end cell row cell y equals short dash 1 over 6 x plus 2 end cell end table

summary
In this lesson, you began with a review of slope and intercepts, because being able to easily identify slopes and intercepts from a graph is very useful when writing the equation to the line. Because you know how to draw a graph from the slope-intercept form, you applied this knowledge to learn how to do this in reverse and determine the slope-intercept form from a graph, by following these steps: 1) determining your y-intercept on the graph; 2) determining your slope using any two points on a line; and 3) writing the equation by plugging the y-intercept and slope values into the slope-intercept form.

Best of luck in your learning!

Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.