Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

What Is a Maximum or a Minimum?

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn about the different kinds of maximum and minimum points on a graph of a function. Specifically, this lesson will cover:

Table of Contents

1. Definitions of Global and Local Maximum and Minimum Points

One of the main uses of derivatives is to find minimum and maximum values of a function, or more simply put, extreme values (or extrema) of a function.

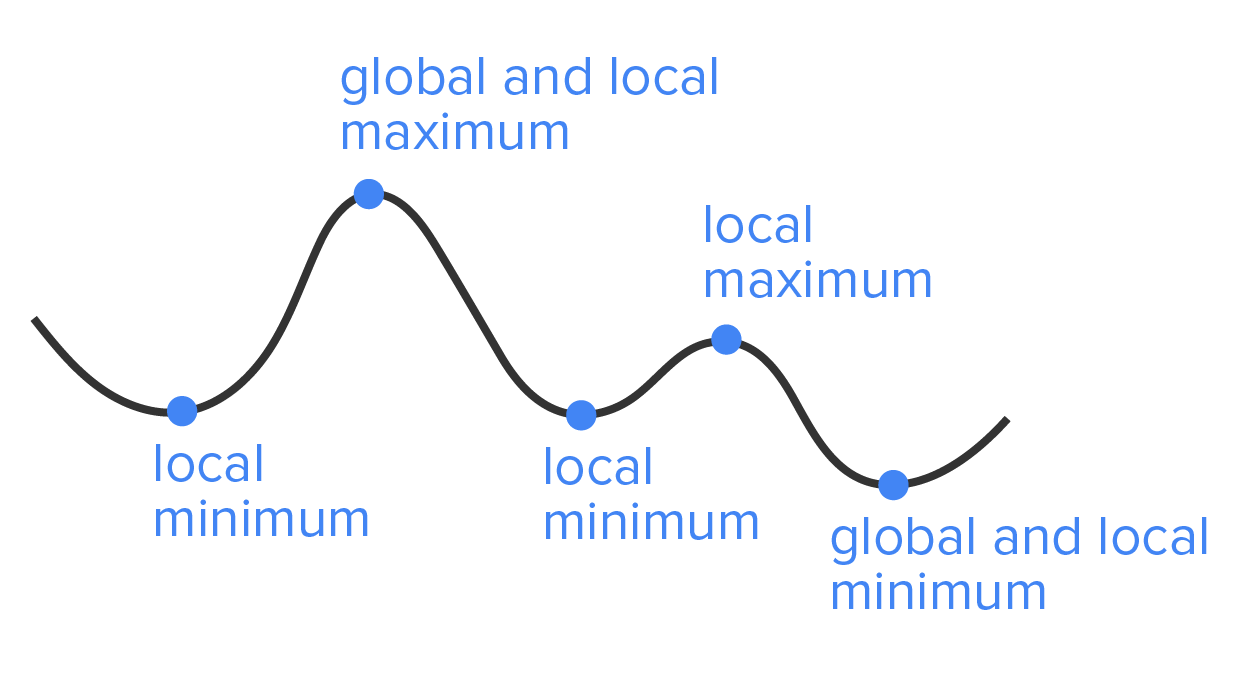
A function can have any one of the following:

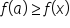  • Global (or Absolute) Maximum: A function f open parentheses x close parentheses has a global (or absolute) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses, and occurs when x equals a.
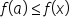  • Global (or Absolute) Minimum: A function f open parentheses x close parentheses has a global (or absolute) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x. In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses, and occurs when x equals a.
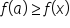  • Local (or Relative) Maximum: A function f open parentheses x close parentheses has a local (or relative) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses for values near x equals a.
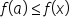  • Local (or Relative) Minimum: A function f open parentheses x close parentheses has a local (or relative) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses for values near x equals a.
The graph shown here summarizes the differences between local and global extrema. Note that the second labeled point (from left to right) is both a local maximum and a global maximum because it meets both conditions: it is both the highest point on the graph and it is the highest point when compared to points immediately to the left and right.

A smooth curve with several peaks, representing local and global extrema of a function. The curve begins from left, falls slightly, and reaches an minimum point at a marked point labeled ‘local minimum’. It then rises to the highest peak at a marked point labeled ‘global and local maximum’. From here, the curve falls sharply to a marked point labeled ‘local minimum’, rises slightly to a smaller peak at a marked point labeled ‘local maximum’, falls again to a marked point labeled ‘global and local minimum’, and extends slightly to the right.

terms to know
Extreme Values
The minimum or maximum values of a function.
Extrema
Another word for extreme values.
Global (or Absolute) Maximum
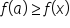A function f open parentheses x close parentheses has a global (or absolute) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses, and occurs when x equals a.
Global (or Absolute) Minimum
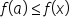A function f open parentheses x close parentheses has a global (or absolute) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x. In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses, and occurs when x equals a.
Local (or Relative) Maximum
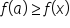A function f open parentheses x close parentheses has a local (or relative) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses for values near x equals a.
Local (or Relative) Minimum
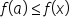A function f open parentheses x close parentheses has a local (or relative) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses for values near x equals a.

2. Finding Global and Local Maximum and Minimum Points

EXAMPLE

Consider the function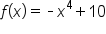 f open parentheses x close parentheses equals short dash x to the power of 4 plus 10 as shown in the graph below.

A graph with an x-axis and a y-axis ranging from −12 to 12. A parabolic curve opening downward rises upward from the third quadrant, crosses the x-axis around (-1.8, 0), reaches a maximum point (0, 10), and then falls sharply into the fourth quadrant, passing through the x-axis at around (1.8, 0).

The highest point on the graph is (0, 10), while there is no lowest point. It is also the highest point when compared to other points around it.

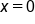Therefore, we say that f open parentheses x close parentheses has a global maximum and local maximum at x equals 0, and its value is 10.

There is no local or global minimum point.

EXAMPLE

Now consider the function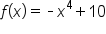 f open parentheses x close parentheses equals short dash x to the power of 4 plus 10, but contained on the interval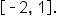 open square brackets short dash 2 comma space 1 close square brackets.

A graph with an x-axis and a y-axis ranging from −12 to 12. A parabolic portion starts from a marked point at (−2, −6) in the third quadrant, rises upward, reaches a maximum point at (0, 10), and then descends to a marked point at (1, 9).

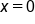The highest point on the graph is (0, 10), which is also the highest point around (0, 10). Therefore, at x equals 0, both a local and global maximum occurs and is equal to 10.

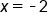The lowest point on the graph is (-2, -6), which means that f open parentheses x close parentheses has a global minimum at x equals short dash 2, which is equal to -6.

Neither (-2, -6) nor (1, 9) are considered local minimum values. This is because there is no graph on the other side of the points to compare.

In other words, having a local extreme point at x equals a means that f open parentheses a close parentheses is the most extreme value on an open interval containing a (both sides of x equals a).

try it
A graph with an x-axis ranging from −100 to 100 and a y-axis ranging from -100 to 100. A parabolic portion starts from a marked point at (1, 130) in the first quadrant, falls sharply to reach another marked point at (8, 32), then rises upward and ends at a marked point at (25, 55.12).

Use the graph to determine all global and local maximum and minimum values of the function.
The global maximum is 130 and it occurs at x equals 1, and both a local and global minimum is 32 at x equals 8.

The point open parentheses 1 comma space 130 close parentheses comma which is the left endpoint, is the highest point on the graph. Therefore, the global maximum value is 130. However, since open parentheses 1 comma space 130 close parentheses is also an endpoint, there is no local maximum value there.

The point open parentheses 8 comma space 32 close parentheses comma is the lowest point on the graph. It is also the lowest point on the graph relative to points on the left and right of it on the graph. Therefore, 32 is the global minimum value and is a local minimum value.

The point open parentheses 25 comma space 55.12 close parentheses comma which is the right endpoint, is neither the highest nor the lowest point on the graph. Since it is also an endpoint, the value 55.12 is neither a global nor local extreme value.

summary
In this lesson, you learned that one of the main uses of derivatives is to find minimum and maximum values of a function. A function can have several types of extreme values, which can be identified from a graph. These points include: global (or absolute) maximum, global (or absolute) minimum, local (or relative) maximum, and local (or relative) minimum. Next, you explored using graphs to find all global and local maximum and minimum values of each respective function.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 3 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Extrema

Another word for extreme values.

Extreme Values

The minimum or maximum values of a function.

Global (or Absolute) Maximum

A function f open parentheses x close parentheses has a global (or absolute) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses, and occurs when x equals a.

Global (or Absolute) Minimum

A function f open parentheses x close parentheses has a global (or absolute) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x. In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses, and occurs when x equals a.

Local (or Relative) Maximum

A function f open parentheses x close parentheses has a local (or relative) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses for values near x equals a.

Local (or Relative) Minimum

A function f open parentheses x close parentheses has a local (or relative) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses for values near x equals a.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.