Table of Contents |
Before we begin discussing weighted average, it may be helpful to review how to calculate the simple average or mean of a data set. In order to find the average, we find the sum of all data values, and then divide by the number of data values in our set.
EXAMPLE
Find the average of the following numbers: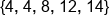 .
.
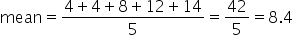

Weighted average is different from simple average in that certain data values carry more weight, or influence the average more heavily. With simple average, every data point is equally represented in the calculation for the mean, but in weighted averages, some data points are multiplied by a number in its calculation.
We use this formula for weighted average:
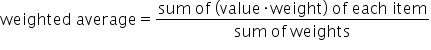
Results Driven: Skill in Action |
Let's see exactly how weighted average pertains to class grades.
EXAMPLE
Suppose that tests and projects account for 50% of your grade, daily assignments represent 30%, and participation is worth 20% of your grade. To calculate your final grade for the class, we multiply your test/project score by its weight of 50%, your assignment score by its weight of 30%, and your participation grade by its weight of 20%, all before adding these figures together. This is illustrated below:| Test/Project Grade: 83% | Assignment Grade: 94% | Participation Grade: 80% |
| Weight: 50% | Weight: 30% | Weight: 20% |
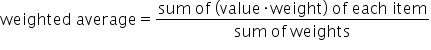
|
Use the formula for weighted average. |
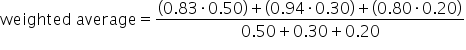
|
Calculate the weighted grade for test/projects, assignments, and participation. |
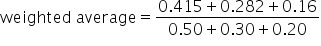
|
Multiply the weight by each value in the numerator. |
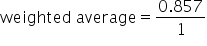
|
Evaluate numerator and denominator. |
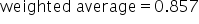
|
Divide 0.857 by 1. |
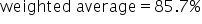
|
Change to a percent. |
Next, we will use the concept of weighted average to set up and solve a mixture problem from the field of chemistry. We'll use this adapted formula as we work through these types of problems:
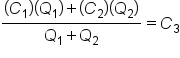
In this formula,
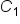 is the concentration of Item 1
is the concentration of Item 1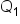 is the quantity of Item 1
is the quantity of Item 1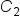 is the concentration of Item 2
is the concentration of Item 2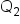 is the quantity of Item 2
is the quantity of Item 2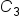 is the concentration of the combined items
is the concentration of the combined items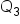 defined.
defined. 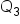 would be the quantity of al the combined items. We technically do see this in our formula in the denominator,
would be the quantity of al the combined items. We technically do see this in our formula in the denominator, 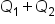 .
.
Problem Solving: Skill Reflect |
EXAMPLE
To prepare for a lab experiment, you mix two concentrations of HCl (hydrochloric acid): 30 mL of 15% HCl solution, and 20 mL of 40% HCl solution. What is the concentration of the mixed solution?
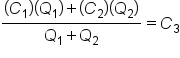
|
Use the formula for weighted average for mixture problems. |
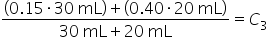
|
Plug in the concentrations and quantities for the two known solutions: 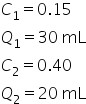
|

|
Multiply each quantity by its weight in numerator. Add quantities in denominator. |
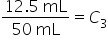
|
Add 4.5 to 8. |
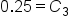
|
Divide by 50 mL. |
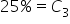
|
Change to a percent |
Some mixture problems will ask us to find specific amounts of each solution that must be mixed together in order to yield a certain amount of a specific concentration. Let's again use the HCl example.
EXAMPLE
We have two kinds of solutions already made: a 15% solution, and a 40% solution. To prepare for a lab experiment, we are going to need 120 mL of a 30% solution. How many mL of each solution must be mixed in order to create this mixture?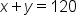 . How does this affect our equation for weighted average?
. How does this affect our equation for weighted average?
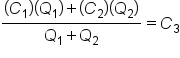
|
Use the formula for weighted average for mixture problems. |
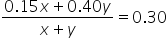
|
Plug in the concentrations for the known solutions: 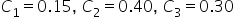
|
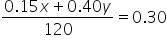
|
Substitute 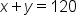
|
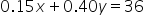
|
Multiply both sides by 120 |
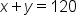 . We can write this equivalently as
. We can write this equivalently as 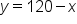 .
.
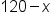 into the original equation instead of y. The result will be a single-variable equation, and we'll be able to solve for x.
into the original equation instead of y. The result will be a single-variable equation, and we'll be able to solve for x.
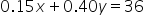
|
The simplified weighted average equation. |
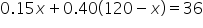
|
Substitute 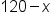 in for y. in for y.
|
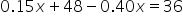
|
Distribute 0.40 into 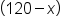 . .
|
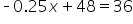
|
Combine like terms. |
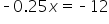
|
Subtract 48. |
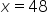
|
Divide by -0.25. |
Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.