Volume

1. Volume Formulas

Volume is the amount of space contained within a three-dimensional object. Shapes such as spheres, prisms, and cylinders are three-dimensional objects that take up a certain amount of space, which we can call its volume. We measure volume in cubic units. Here are some examples of cubic measurements:

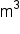
	cubic meters
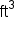
	cubic feet
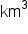
	cubic kilometers

With these measurements, we can easily tell they are cubic measurements because they include an exponent of three. Not all cubic measurements have this visual clue. For example, the liter is abbreviated with the letter L, and does not contain an exponent of three, yet it is a cubic measurement (it measures liquid volume, and is actually equivalent to 1000 cubic centimeters).

There are several formulas for finding the volumes of different shapes. We are going to focus on the volumes of a rectangular prism, cylinder, and sphere. Here are the formulas to know:

formula to know

Volume of a Rectangular Prism

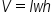, where V is volume, l is length, w is width, and h is height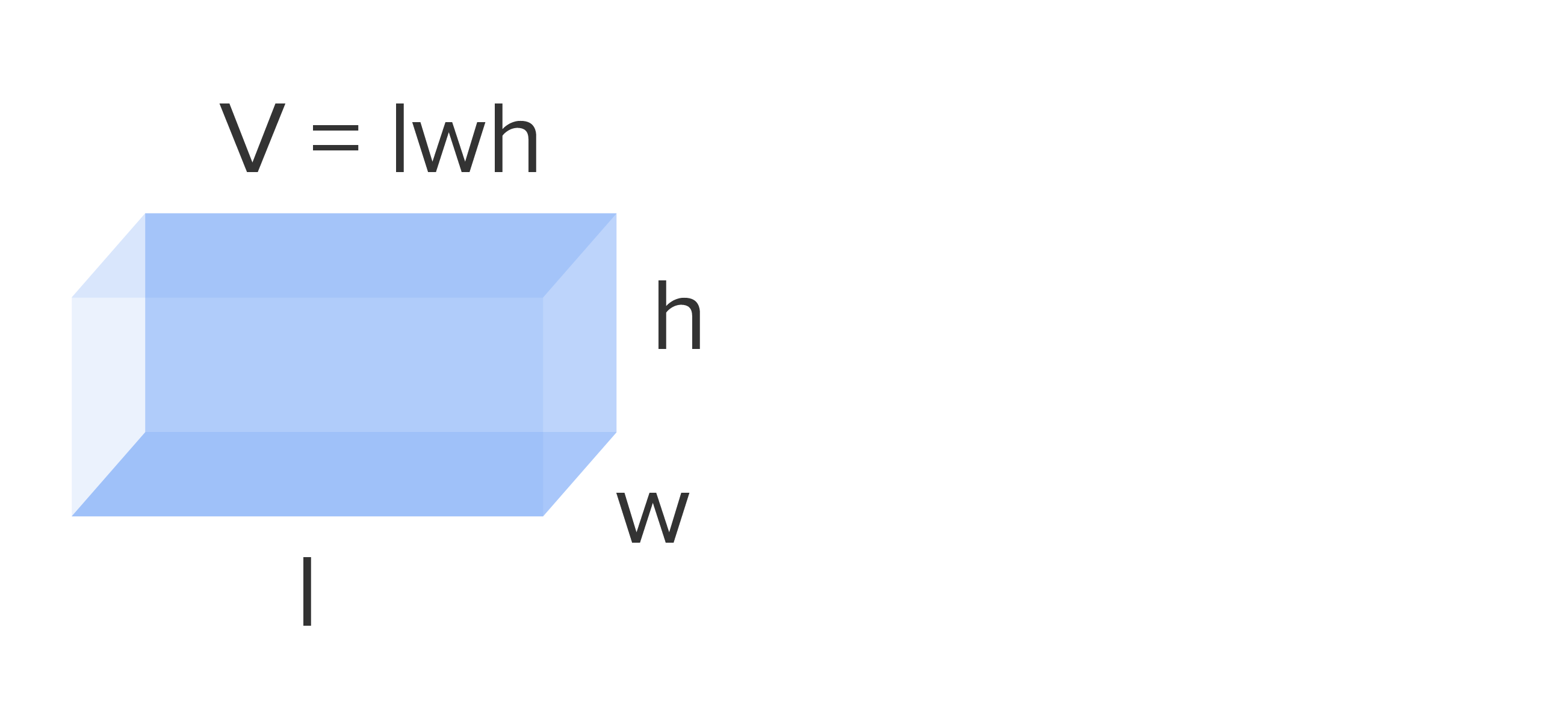

EXAMPLE

Take a look at the figure below: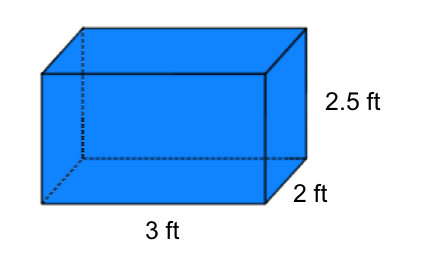



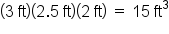
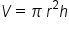To find the volume, we simply multiply all of the dimensions together. This includes the units of measurement.

formula to know

Volume of a Cylinder

, where V is volume, r is the radius of the circular base, h is height, and π is approximately 3.14

EXAMPLE

Find the volume of the following cylinder: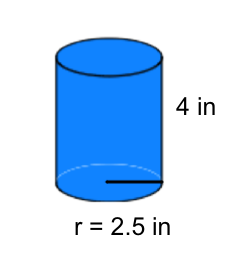



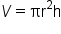
To find the volume, we first square the radius of the circular base, and then we multiply by pi and the height. Remember that the order of operations dictates exponents before multiplication, so that's why we square the radius before multiplying anything.

	Formula for the volume of a cylinder
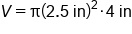
	Substitute radius length and height
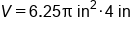
	Square the radius
	Multiply by 4 inches
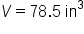
	Our Solution, using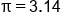

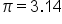
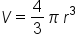hint

Notice that some of these formulas include the number, pi. Pi is an important number. Pi is a constant irrational number equal to 3.14159265… If you need to give a decimal approximation, use

formula to know

Volume of a Sphere

, where V is volume, r is the radius, and π is approximately 3.14

EXAMPLE

Find the volume of the sphere pictured below: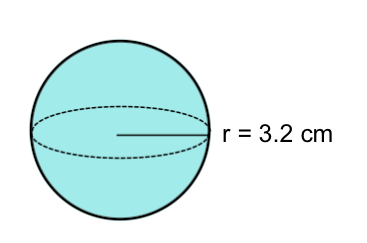



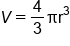
The only piece of information we are given is the radius of the sphere, but this is all we need to calculate the volume. Just like with the volume of a cylinder, first we apply the exponent. After cubing the radius, we multiply it by pi and then by four-thirds.

	Formula for the volume of a sphere
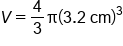
	Substitute radius length
	Cube the radius
	Multiply by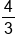
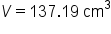
	Our Solution, using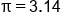

hint

To leave your answer as an exact value, you can choose to leave pi as π multiplied by a number. If you need to give a decimal approximation, use π = 3.14.

term to know

Pi

The ratio of a circle's circumference to its diameter; approximately equal to 3.14.

2. Finding Side Lengths or Radii Given the Volume

In our previous examples, we used given measurements for side lengths and radii to calculate the volume of a three-dimensional object. In the following examples, we are going to use a given measurement of volume to calculate a side length or a radius. We will use the same formulas, but in a different way.

EXAMPLE

Find the side length of a rectangular prism: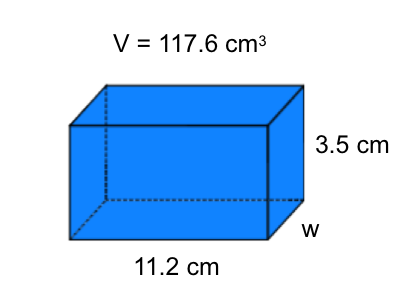



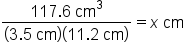
Dividing both sides of the equation by the length and the height will do two things: first, it will cancel the length and the width from one side of the equation, leaving just an expression for the width.

Second, it can help us cancel the cubic units on the other side if the equation, leaving our answer in linear centimeters. (Linear centimeters just means regular centimeters we are used to measure. We would only say "linear" if we wanted to make it clear that it isn't square centimeters or cubic centimeters.)

Now we can perform the numeric division on the left side of the equation. This is our solution for the width of the prism:

	Divide volume by length and height
	Simplify denominator
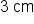
	Our Solution

Lastly, let's use a volume formula to solve for an unknown radius.

EXAMPLE

Find the radius for the sphere below: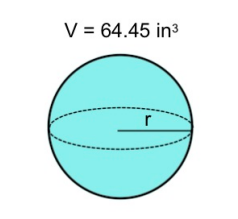



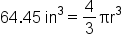
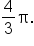We are given the volume as 65.45 cubic inches, with an unknown radius. Substituting known information into the formula for the volume of a sphere, we have:

How can we isolate r? Look at the numbers and operations surrounding the variable r. It is being raised to the power of 3, and then multiplied by We need to undo this by applying inverse operations, but also in reverse order. This means first we need to undo the multiplication by 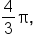and then undo the power of 3.

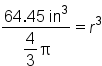
	Volume of a Sphere Formula
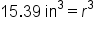
	Divide both sides by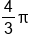
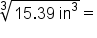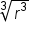
	Apply the cube root of both sides
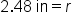
	Our Solution

hint

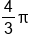Note that is a number, so it can be divide in one step. One strategy is to evaluate 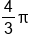first and then divide it through both sides of the equation. Another strategy is to divide by 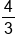first (or multiply by the reciprocal), and then divide by pi. You could also first divide by pi, and then divide by 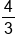(or multiply by the reciprocal). These are all valid methods.