Table of Contents |
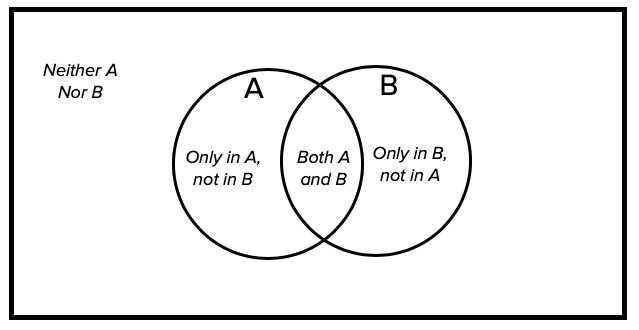
Venn diagrams are an important idea in probability theory. Venn diagrams were invented by the logician John Venn. They're useful for understanding the relationships between two different sets of objects or two different events in probability.
A typical Venn diagram with two intersecting sets has four parts to it:
EXAMPLE
Suppose that in a high school of 80 students, 18 of them take statistics, 15 take economics, and 8 students take both.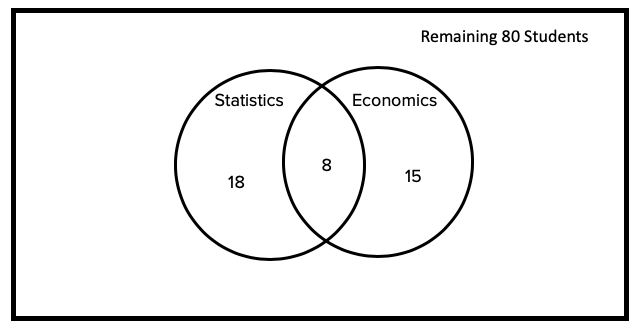
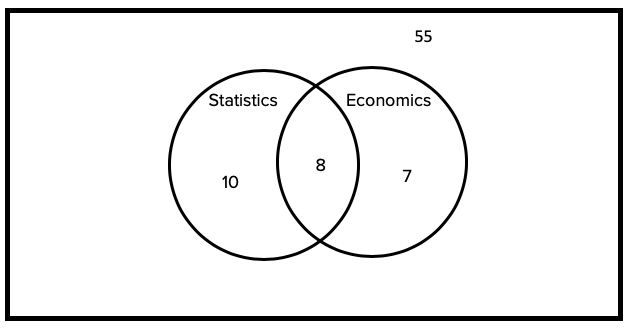
We can also show complements in a Venn diagram. Complements are everything that's not in a particular event.
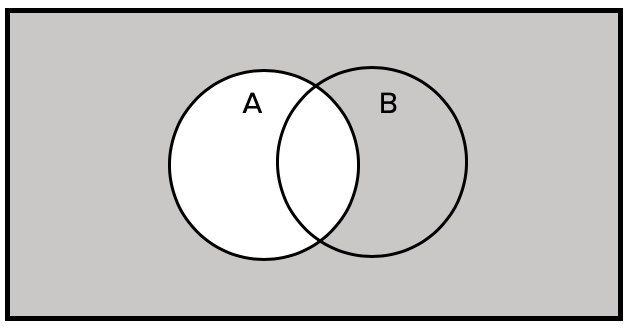
The complement of A is everything outside of the A bubble, including the part of B that does not overlap with A.
The overlapping portion is in A, so it is therefore not part of the complement.
Not all Venn diagrams need overlap like this. Sometimes, the two events, A and B, don't have any outcomes in common, which looks like this:
EXAMPLE
Suppose A is the event of rolling an even number and B is the event of rolling a 5. There's no overlap between the two ideas, so you can draw the bubbles as separate. In the "neither" category would be any rolls that are odd but not 5, which leaves 1 and 3.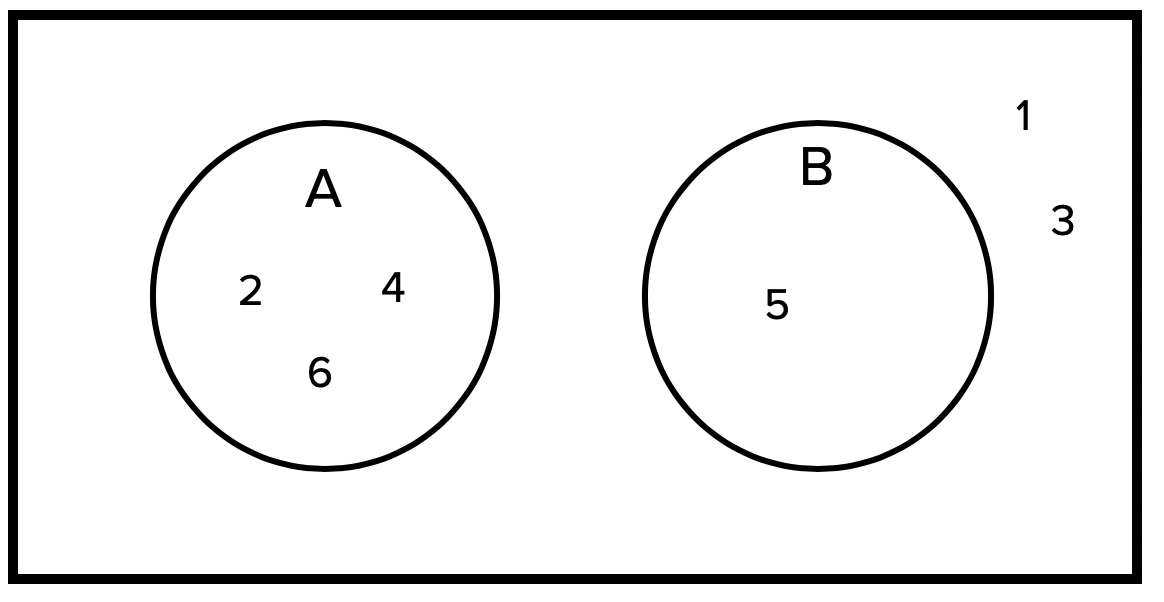
Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.