Valid Rules of Inference, Part 2 (Inferences From Conjunctions and Disjunctions)

1. Rules of Inference for Conjunction

In this tutorial, we’ll learn rules of inference for conjunctions and disjunctions. Let’s look at conjunctions first. Remember that a conjunction is only true if both conjuncts are true.

1a. Conjunction Elimination

Since you have already seen an elimination rule, you may guess that Conjunction Elimination involves reducing a conjunction to one of its conjuncts. In other words, if we know a conjunction is true, we are immediately licensed to infer the truth of either of the conjuncts. This is because a conjunction is true only when both conjuncts are true.

1. p ∧ q
2. ∴ p

Consider this example in natural language:

I have a refrigerator and a freezer.

Therefore, I have a freezer.

While it may seem too obvious an inference to need a rule, it is often necessary in proofs to isolate one of the conjuncts for a derivation. Each step in the proof should be as obvious as possible. Even though Conjunction Elimination is so obvious you might want to skip it, it should always be included because proofs are a step-by-step process. Remember that while we are using single letters as propositional variables above, each variable might represent a complex sentence of its own, and simplification will be a help in comprehending the proof.

The notation we will use for Conjunction Elimination in our proof is ∧E. Unlike the rules we’ve seen so far, this one will refer to a single previous sentence in the proof. (So, this rule is NOT a syllogism!)

key concept

∧E

The notation used in a proof to show the rule of Conjunction Elimination has been applied to derive the new sentence.

term to know

Conjunction Elimination

A rule of inference stating that if we have a true conjunction (p ∧ q), we are licensed to infer the truth of either conjunct.

1b. Conjunction Introduction

The partner to Conjunction Elimination is called Conjunction Introduction. As a rule of inference, Conjunction Introduction means that if you have two different sentences established as true in the proof, then you can infer that their conjunction is also true:

1. p
2. q
3. ∴ p ∧ q

In natural language, we might call it a paraphrase that pairs two previous statements.

I have a son.

I have a daughter.

I have a son and a daughter.

As with Conjunction Elimination, this may seem a bit obvious, but remember again: the steps in a proof are meant to be simple, but cumulatively they help us see less obvious inferences. Also remember that for any of these rules, the concepts can represent complex sentences, and thus simplification might be warranted.

key concept

∧I

The notation used in a proof to show the rule of Conjunction Introduction has been applied to derive the new sentence.

term to know

Conjunction Introduction

A rule of inference stating that if we have two true sentences (p, q), we are licensed to infer the truth of their conjunction (p ∧ q).

---

2. Rules of Inference for Disjunctions

In natural language, statements with “or” can be either inclusive (compatible with both disjuncts being true) or exclusive (incompatible with both disjuncts being true). In logic, “or” is inclusive, unless otherwise stated explicitly (e.g., by “and not both” language). This is essential to keep in mind when understanding the next rule of inference.

2a. Disjunctive Syllogism

Disjunctive Syllogism is a rule of inference stating that if we know a disjunction is true, and we know the negation of one of the disjuncts is also true, then we infer that the other disjunct is true.

1. p ∨ q
2. ¬p
3. ∴q

As with all rules of inference, the propositional variables in the general rule may be substituted for complex sentences:

1. ¬A ∨ (B ∧ C)
2. ¬¬A
3. ∴ B ∧ C

The first premise here is a disjunction of two complex sentences. Remember that a negation is by itself a complex sentence because it includes both an atomic sentence and a truth-functional operator. The second premise is a negation of one of the disjuncts, ¬¬A, which is equivalent to A. So, from the two premises, we can conclude (by Disjunctive Syllogism) that the second disjunct must be true.

In natural language, you may see Disjunctive Syllogism in such exchanges as this:

Diner: I’ll have either the roast beef or the shrimp.

Server: We’re all out of shrimp.

Diner: Then I’ll have the roast beef!

Disjunctive Syllogism is noted in a proof as DS.

key concept

DS

The notation used in a proof to show the rule of Disjunctive Syllogism has been applied to derive the new sentence.

Because logical disjunction is “inclusive,” Disjunctive Syllogism won’t help us if one of the disjuncts is known to be true. In the example below, the argument is not valid, because there’s no premise stating that one of the disjuncts is false, so we can’t derive the other disjunct.

term to know

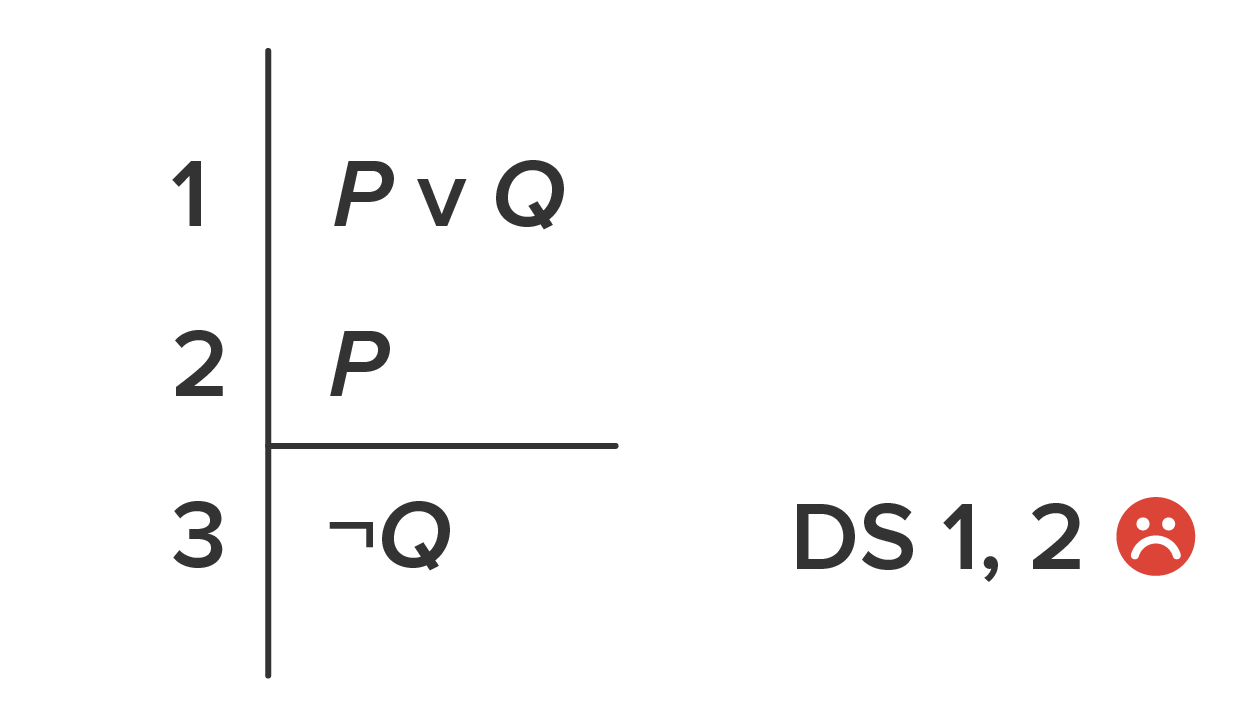
Disjunctive Syllogism

A rule of inference stating that if we know a disjunction is true, and we know the negation of one of the disjuncts is also true, then we infer that the other disjunct is true.

2b. Disjunction Introduction

The next rule we’ll introduce is called Disjunction Introduction. Once you understand the conditions under which a disjunction is true, then it will clarify why this form of inference is valid. Disjunction Introduction has the following form:

1. p
2. ∴ p ∨ q

What this rule says, in words, is that if we have established that a sentence (p) is true, then we are licensed to infer the truth of a novel disjunction with that sentence as a disjunct (p ∨ q), where q can be anything we want! In natural language, we might see a statement like this:

I have a cat, so yes, I have a cat or a dog.

You may easily see the logical part of this. Of course if you have a cat, then it is factually true to say you have a cat or a dog. It is also factually correct to say you have a cat or a possum, a cat or a dragon, or a cat or a sarlacc (the giant sandworm in Star Wars: Return of the Jedi). The disjunction only means that at least one of the statements is true, and the cat part is true, so there is no way for the disjunction to be false, no matter how far-fetched the other disjunct is.

The harder thing to understand about this rule is why we would ever want to use it. Why say you have a cat or a dog if we already know it’s a cat? Sometimes there might be a part of our conclusion that isn’t already part of our proof. By being able to introduce it in a disjunction through Disjunction Introduction, we might be able to make the necessary bridge to get us the rest of the way to the conclusion.

As with every rule of inference, remember that it also applies to complex propositions.

1. A → B
2. ∴ (A → B) ∨ (B → C)

key concept

∨I

The notation used in a proof to show the rule of Disjunction Introduction has been applied to derive the new statement.

term to know

Disjunction Introduction

A rule of inference stating that if we have established that a sentence (p) is true, then we are licensed to infer the truth of a novel disjunction with that sentence as a disjunct (p ∨ q) where q can be anything we want!

---

3. DeMorgan’s Laws

The final of our rules of inference comprises DeMorgan’s Laws, and you already know it! We learned it in the last challenge, as logical equivalence. These rules of inference support “pushing” a negation sign inside or outside of parentheses and “flipping the sign,” turning a disjunction into a conjunction or vice versa. These are logical equivalencies.

• A negated disjunction ¬(p ∨ q) is logically equivalent to the conjunction of the negated disjuncts ¬p ∧ ¬q.
• A negated conjunction ¬(p ∧ q) is logically equivalent to the disjunction of the negated conjuncts ¬p ∨ ¬q.
• A conjunction of negated sentences ¬p ∧ ¬q is logically equivalent to a negated disjunction of the (non-negated) conjuncts ¬(p ∨ q).
• A disjunction of negated sentences ¬p ∨ ¬q is logically equivalent to the negated conjunction of the (non-negated) disjuncts ¬(p ∧ q).

Remember these examples from an earlier tutorial:

Carla won’t have cake or ice cream.

Carla won’t have cake and won’t have ice cream.

These are two ways of expressing the same idea, that Carla is having neither cake nor ice cream. Similarly, these two statements say she might have one but not both.

Carla won’t have cake and ice cream.

Carla won’t have cake or won’t have ice cream.

DeMorgan’s Laws are unique because they can be applied both ways, meaning that if we have the sentence ¬(p ∨ q), we can apply DeMorgan’s Laws to add the sentence (¬p ∧ ¬q), but we can also add the sentence ¬(p ∨ q) if we have the sentence (¬p ∧ ¬q). In all cases, we “push” the negation sign inside or outside of the parentheses (which we may need to add) and “flip the sign” (conjunction to disjunction or vice versa). This is a helpful way to remember how DeMorgan’s Laws work.

DeMorgan’s Laws can be very useful in combination with our other rules of inference. For example, say you have a proof with the sentence:

A → B

And you also have the sentence:

¬(B ∨ C)

Using a series of sentences, we can show that A is false.

try it

You don’t need to write it out, but consider how you would prove that A is false in this case. Just try to think it through.

Check Your Answer

This will take three rules of inference to complete.

1. First, we apply DeMorgan’s Laws to ¬(B ∨ C) to get ¬B ∧ ¬C.
2. Next, we use Conjunction Elimination to get ¬B from ¬B ∧ ¬C.
3. Last, we apply Modus Tollens to A → B, having shown ¬B.
4. This results in ¬A.

key concept

DeM

The notation used in a proof to show DeMorgan’s Laws were applied.

term to know

DeMorgan’s Laws

The rules of inference governing four logical equivalences.

• A negated disjunction ¬(p ∨ q) is logically equivalent to the conjunction of the negated disjuncts ¬p ∧ ¬q.
• A negated conjunction ¬(p ∧ q) is logically equivalent to the disjunction of the negated conjuncts ¬p ∨ ¬q.
• A conjunction of negated sentences ¬p ∧ ¬q is logically equivalent to a negated disjunction of the (non-negated) conjuncts ¬(p ∨ q).
• A disjunction of negated sentences ¬p ∨ ¬q is logically equivalent to the negated conjunction of the (non-negated) disjuncts ¬(p ∧ q).