Table of Contents |
How do we as rational consumers know that we have maximized our satisfaction from the decisions that we make? We can quantify our satisfaction by placing numerical values on the level of satisfaction we receive from consuming goods and services. Utility is the term economists use to describe the satisfaction or happiness a person gets from consuming a good or service. The artificial unit of measurement of satisfaction is called a util—short for utility. A util is a measurement that exists only in the imagination of economists when considering scenarios involving consumer choice.
EXAMPLE
Suppose you’re a lover of a specific brand of shoes. You located an online shop selling the shoes you want at a price that fits into your budget. You place the order and the shoes arrive. The shoes are very comfortable, and you begin thinking about ordering a second pair of the exact same style. Would you be as willing to pay the same price for a second or third purchase of the shoe? If you are like most shoppers, the first purchase of a good or service provides the most satisfaction. An additional purchase of the same item would make you happy but not quite as much as the one before it. But a slight drop in price might help restore your sense of satisfaction with that next purchase. This response aligns with the law of demand to explain your buying response.When considering utility, a key assumption is that utility can not be measured by an outside party but only by the individual deciding between alternatives. Utility will be different for different individuals. We don't all enjoy the same thing(s) to the same level; therefore, we won't get the same amount of satisfaction out of the same things. In the content that follows, we will assign numeric util values to represent the satisfaction achieved by making different choices to determine the rational consumer’s optimal choice. Satisfaction will be equated to utility.
In the first three tutorials of this Challenge, we used a simplified model of a two-good economy to explore consumer choice. You learned that indifference curves represent a consumer's preferences and that the budget line accounts for both the price of the product and the total budget available. You also learned how to determine consumer choice graphically using indifference curves and budget lines. This lesson explores the exact same concepts but will do so mathematically rather than graphically.
Consider the following scenario. Suppose that Andres enjoys both cheese quesadillas and chicken fajitas. These are his two most preferred food choices. How many of each will Andres consume? Would this be the same for everyone? Obviously not. Different consumers will have different preferences, and individual preferences affect the level of satisfaction obtained from consuming cheese quesadillas versus chicken fajitas. Andres’ goal as a consumer, however, has not changed. He wishes to maximize his utility (satisfaction), given his personal preferences, product prices, and his income.
As you have learned, utils are artificial units of measurement used to measure the satisfaction a particular choice brings an individual. We will now measure how much total satisfaction Andres receives from his particular choices.
Andres is choosing between chicken fajitas and cheese quesadillas. In the table below, columns 1 and 3 show the quantity of chicken fajitas and the quantity of cheese quesadillas. In columns 2 and 4, there are values that indicate how much total satisfaction Andres experiences from consuming that particular number of chicken fajitas or that particular number of cheese quesadillas.
|
Quantity of
Chicken Fajitas (1) |
Total Utility (2) |
Quantity of
Cheese Quesadillas (3) |
Total Utility (4) |
|
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 1 | 22 | 1 | 16 | |
| 2 | 43 | 2 | 31 | |
| 3 | 63 | 3 | 45 | |
| 4 | 81 | 4 | 58 | |
| 5 | 97 | 5 | 70 | |
| 6 | 105 | 6 | 81 | |
| 7 | 100 | 7 | 86 |
In the first row of the table above, you can see that when Andres consumes no chicken fajitas and no cheese quesadillas, he experiences a zero level of total satisfaction from eating zero chicken fajitas or zero cheese quesadillas. This makes sense. You can’t enjoy something you don’t have. His total utility is zero in the first row of column 2 and 4 of the table.
In the second row of the table, you can see that when Andres consumes one chicken fajita, his satisfaction or total utility reaches 22 utils (column 2).
In the third row of the table, when Andres consumes 2 chicken fajitas, his total utility or satisfaction is 43 utils (column 2). In the final row of the table, Andres’ total satisfaction from consuming 7 chicken fajitas would be 100 utils (bottom of column 2) and his total utility for consuming 7 cheese quesadillas would be 86 utils (column 4 bottom of column).
Total utility is the total amount of satisfaction that is received from consuming or choosing a particular quantity of a good or service. Total utility is expressed as a quantity of utils.
Let’s consider a visual representation of the relationship between quantity consumed and total utility. In the graph below, the quantity of chicken fajitas is on the x-axis and total utility is on the y-axis. A pattern typical in economics emerges.
The graph below shows the total utility of the chicken fajitas increasing with each additional unit of the good consumed. At 6 chicken fajitas, Andres’ total utility has reached its maximum, or peak, and then begins to decline. You can check the table to verify this. Why does total utility begin to decline? Isn’t chicken fajitas one of his most favorite foods?
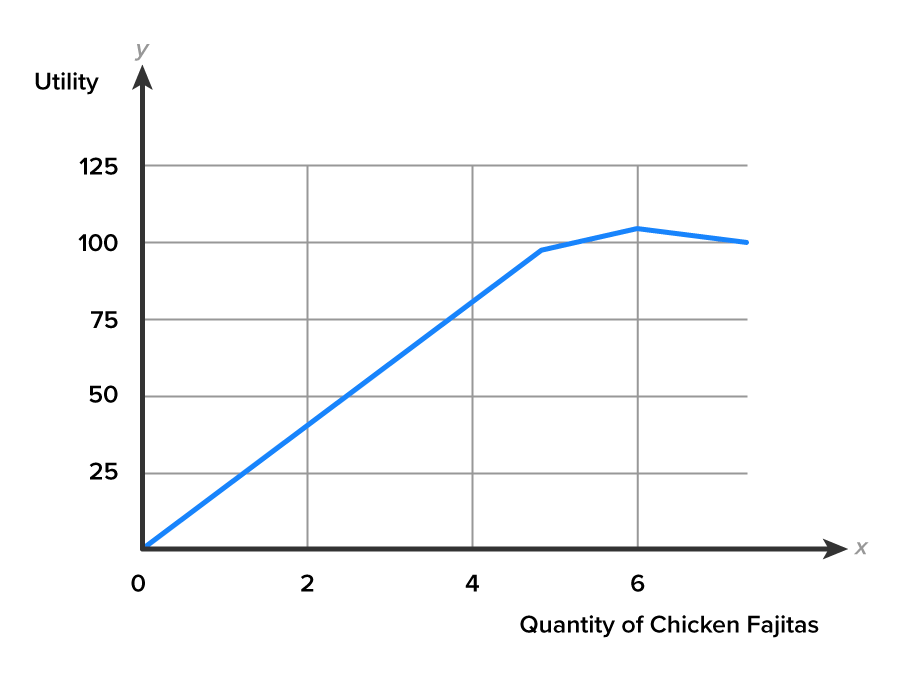
Put yourself in Andres’ shoes and think about how you would feel if you consumed increasing numbers of the same item. Your enthusiasm, even for your favorite item, is likely to decline.
Your first chicken fajita would likely make you very happy. Your second chicken fajita would make you happy but probably not as happy as the first chicken fajita. Your happiness would dip a bit further after the third chicken fajita. By the sixth chicken fajita, your happiness is likely lower than your happiness on the fourth one. By the time you consider a seventh chicken fajita, just thinking about eating it makes your stomach feel queasy. Your satisfaction declines over time with each additional chicken fajita you consume.
Let’s compare how Andres’ total utility changes as he consumes each additional chicken fajita. We will be calculating marginal utility, which is the additional utility provided by each additional unit consumed.
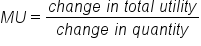
To calculate marginal utility, begin with row 2 in the table below. In row 2, you can see that the first chicken fajita provides Andres with 22 total utils of satisfaction. This is the total utility. To calculate marginal utility:
|
Quantity of Chicken Fajitas (1) |
Total Utility (2) |
Marginal Utility (3) |
|---|---|---|
| 0 | 0 | |
| 1 | 22 | (22 - 0) / (1-0) = +22 utils / +1 fajita |
| 2 | 43 | (43 - 22) / (2-1) = +21 utils / +1 fajita |
| 3 | 63 | |
| 4 | 81 | |
| 5 | 97 | |
| 6 | 105 | |
| 7 | 100 |
As you can see in the preceding and following calculations, marginal utility is positive (+) for each additional chicken fajita up to the seventh one, at which time the additional utility turns negative (-5 utils).
By adding up the marginal values (22 + 21 + 20 + 18 + 16 + 8 - 5), you can determine the total utility Andres receives from consuming 7 chicken fajitas (100 utils)
Consider the following table, which includes both the total utility and the marginal utility numbers.
|
Quantity of Chicken Fajitas (1) |
Total Utility (2) |
Marginal Utility (3) |
|---|---|---|
| 0 | 0 | |
| 1 | 22 | 22 |
| 2 | 43 | 21 |
| 3 | 63 | 20 |
| 4 | 81 | 18 |
| 5 | 97 | 16 |
| 6 | 105 | 8 |
| 7 | 100 | -5 |
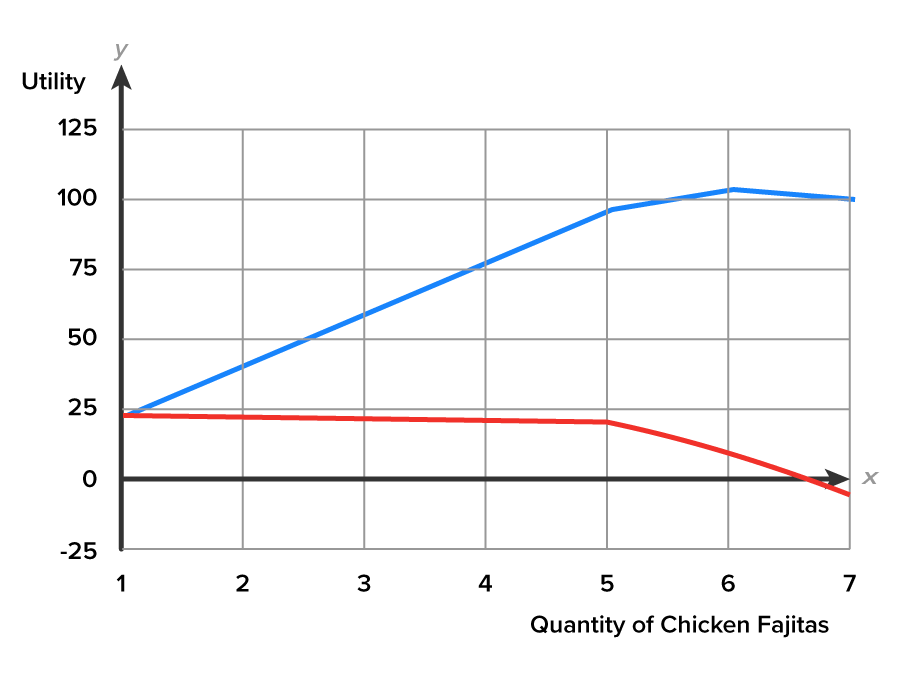
A pattern emerges if we scan down the marginal utility column. Unlike total utility, which increases until the seventh chicken fajita, the marginal utility values diminish as additional units of the good are consumed. Notice that each subsequent chicken fajita consumed provides less additional utility or satisfaction than the one before it. For example:
Diminishing marginal utility is another example of the more general law of diminishing returns that we learned about earlier in this Challenge.
Graphing marginal utility against quantity reveals this pattern of diminishing marginal utility. Total utility follows the pattern of increasing until it hits its peak, or maximum value, while marginal utility shows a general pattern of decreasing and crossing the horizontal x-axis when total utility turns negative.
We now know that Andres is a utility-maximizing consumer. He has preferences to which he has assigned utility values, known as utils. Andres, like all consumers, must take into account his income while maximizing utility. We will now take Andres’ budget into consideration. He has a budget of $56 to purchase dinners each day for a week. The price for each chicken fajita is $14 and the price for each cheese quesadilla is $7.
Our formula for marginal utility will now account for the price of each product to allow for comparisons between two goods or services. You can use the following formula to calculate the marginal utility per the price, or additional dollar spent.
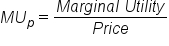
Using marginal utility per the price formula, we will calculate the added units of satisfaction per the dollar spent on the good or service. In this lesson, we have assumed that Andres is a rational individual. He will make his decisions using facts and following sensible rules.
To make an optimal decision, one compares how costs and benefits change from one option to the next. Examining the added benefit and added cost of choosing a little more or a little less of something is known as marginal analysis. You might think of marginal analysis as the analysis of change from one unit to the next unit.
Returning to our example, we will perform the calculation for marginal utility per the price. The price of a chicken fajita is $14. The marginal utility of a chicken fajita is shown in column 3 of the table below. To perform the marginal utility per the price calculation, divide the marginal utility (MU) value in column 3 by the price of the good, which is $14 per chicken fajita. Column 5 shows the results of the calculation: the marginal utility per the price of the good.
| Price $14.00 | ||||
|---|---|---|---|---|
|
Quantity of Chicken Fajitas (1) |
Total Utility (2) |
Marginal Utility (3) |
Marginal Utility per the Price (4) |
MU
per Price ($) (5) |
| 0 | 0 | - | - | - |
| 1 | 22 | 22 | 22/$14 | +1.57 utils per dollar |
| 2 | 43 | 21 | 21/$14 | +1.50 utils per dollar |
| 3 | 63 | 20 | 20/$14 | +1.43 utils per dollar |
| 4 | 81 | 18 | 18/$14 | +1.00 utils per dollar |
| 5 | 97 | 16 | 16/$14 | +1.14 utils per dollar |
| 6 | 105 | 8 | 8/$14 | +0.57 utils per dollar |
| 7 | 100 | -5 | -5/$14 | -0.36 utils per dollar |
Given the price of the fajita, Andres receives +1.57 units of satisfaction per dollar spent for the first chicken fajita. His second chicken fajita provides an additional 1.50 units of satisfaction per dollar spent. His third chicken fajita provides 1.43 added units of satisfaction per dollar spent. And so on.
As a rational consumer, Andres will follow the simple rule of equating margins to achieve maximum satisfaction from his purchases. To maximize his utility, Andres will equate the marginal utilities per the price of the items. He will compare the added utility received from consuming the additional item per the last dollar spent. This is the concept considered in the next lesson.
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM LUMEN LEARNING’S “Microeconomics”. ACCESS FOR FREE AT https://courses.lumenlearning.com/wm-microeconomics/. LICENSE: CC ATTRIBUTION 4.0 INTERNATIONAL.