Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Using Tables to Find Antiderivatives

Author: Sophia
PDF Version

what's covered
In this lesson, you will use a table of integrals to find antiderivatives and solve problems that cannot be solved only using the formulas and techniques learned thus far. Specifically, this lesson will cover:

Table of Contents

1. Using a Table to Find Antiderivatives

Given any function, we have the necessary tools to find its derivative.

But to find antiderivatives of many functions, new techniques are required. Since these techniques are not covered in this course, we will make use of the table of integrals as referenced below.

File:39085-Table of Integrals - Page 1.jpg

Table of Integrals Page 1

File:39086-Table of Integrals - Page 2.jpg

Table of Integrals Page 2

File:39087-Table of Integrals - Page 3.jpg

Table of Integrals Page 3

File:39088-Table of Integrals - Page 4.jpg

Table of Integrals Page 4

EXAMPLE

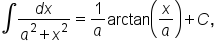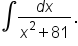
Assuming a is a constant, use formula #44, which is integral fraction numerator d x over denominator a squared plus x squared end fraction equals 1 over a arctan open parentheses x over a close parentheses plus C comma to find integral fraction numerator d x over denominator x squared plus 81 end fraction.

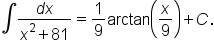
Using the formula as a model, we see that a equals 9. Then, integral fraction numerator d x over denominator x squared plus 81 end fraction equals 1 over 9 arctan open parentheses x over 9 close parentheses plus C.

Here is another example, this time using logarithmic functions.

EXAMPLE

Find the indefinite integral: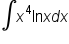 integral x to the power of 4 ln x d x

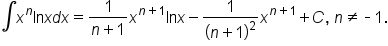
According to formula #38 in the integral table, integral x to the power of n ln x d x equals fraction numerator 1 over denominator n plus 1 end fraction x to the power of n plus 1 end exponent ln x minus 1 over open parentheses n plus 1 close parentheses squared x to the power of n plus 1 end exponent plus C comma space n not equal to short dash 1.

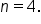
Therefore, use this formula with n equals 4.

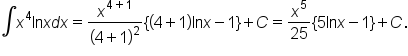
Then, integral x to the power of 4 ln x d x equals x to the power of 4 plus 1 end exponent over open parentheses 4 plus 1 close parentheses squared open curly brackets open parentheses 4 plus 1 close parentheses ln x minus 1 close curly brackets plus C equals x to the power of 5 over 25 open curly brackets 5 ln x minus 1 close curly brackets plus C.

try it
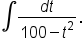
Consider integral fraction numerator d t over denominator 100 minus t squared end fraction.
Find the antiderivative by using formula #46 in the table.
Formula #46 states that integral fraction numerator 1 over denominator a squared minus x squared end fraction d x equals fraction numerator 1 over denominator 2 a end fraction ln open vertical bar fraction numerator x plus a over denominator x minus a end fraction close vertical bar plus C

In this case, a equals 10 comma so we have:

integral fraction numerator 1 over denominator 10 squared minus t squared end fraction d t equals fraction numerator 1 over denominator 2 open parentheses 10 close parentheses end fraction ln open vertical bar fraction numerator t plus 10 over denominator t minus 10 end fraction close vertical bar plus C equals 1 over 20 ln open vertical bar fraction numerator t plus 10 over denominator t minus 10 end fraction close vertical bar plus C

EXAMPLE

Use an appropriate formula to find the indefinite integral: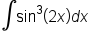 integral sin cubed open parentheses 2 x close parentheses d x

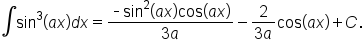
According to formula #24, integral sin cubed open parentheses a x close parentheses d x equals fraction numerator short dash sin squared open parentheses a x close parentheses cos open parentheses a x close parentheses over denominator 3 a end fraction minus fraction numerator 2 over denominator 3 a end fraction cos open parentheses a x close parentheses plus C.

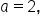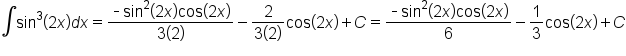
With a equals 2 comma we have: integral sin cubed open parentheses 2 x close parentheses d x equals fraction numerator short dash sin squared open parentheses 2 x close parentheses cos open parentheses 2 x close parentheses over denominator 3 open parentheses 2 close parentheses end fraction minus fraction numerator 2 over denominator 3 open parentheses 2 close parentheses end fraction cos open parentheses 2 x close parentheses plus C equals fraction numerator short dash sin squared open parentheses 2 x close parentheses cos open parentheses 2 x close parentheses over denominator 6 end fraction minus 1 third cos open parentheses 2 x close parentheses plus C

2. Using a Table to Solve Applications Involving Definite Integrals

Since the key step in evaluating 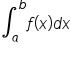integral subscript a superscript b f open parentheses x close parentheses d x is finding the antiderivative of 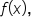f open parentheses x close parentheses comma we can solve area and distance problems using the tables of integrals when necessary.

EXAMPLE

Evaluate the definite integral: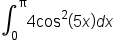 integral subscript 0 superscript straight pi 4 cos squared open parentheses 5 x close parentheses d x

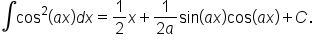
According to formula #19 in the table, integral cos squared open parentheses a x close parentheses d x equals 1 half x plus fraction numerator 1 over denominator 2 a end fraction sin open parentheses a x close parentheses cos open parentheses a x close parentheses plus C.

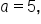In our integral, a equals 5 comma which means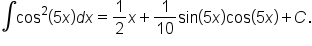 integral cos squared open parentheses 5 x close parentheses d x equals 1 half x plus 1 over 10 sin open parentheses 5 x close parentheses cos open parentheses 5 x close parentheses plus C.

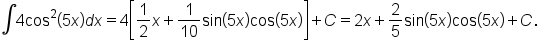
Then, integral 4 cos squared open parentheses 5 x close parentheses d x equals 4 open square brackets 1 half x plus 1 over 10 sin open parentheses 5 x close parentheses cos open parentheses 5 x close parentheses close square brackets plus C equals 2 x plus 2 over 5 sin open parentheses 5 x close parentheses cos open parentheses 5 x close parentheses plus C.

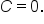To use the fundamental theorem of calculus, use C equals 0. This leads to:

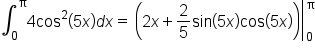
integral subscript 0 superscript straight pi 4 cos squared open parentheses 5 x close parentheses d x equals open open parentheses 2 x plus 2 over 5 sin open parentheses 5 x close parentheses cos open parentheses 5 x close parentheses close parentheses close vertical bar subscript 0 superscript straight pi
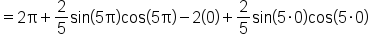
equals 2 straight pi plus 2 over 5 sin open parentheses 5 straight pi close parentheses cos open parentheses 5 straight pi close parentheses minus 2 open parentheses 0 close parentheses plus 2 over 5 sin open parentheses 5 times 0 close parentheses cos open parentheses 5 times 0 close parentheses
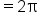
equals 2 straight pi

Thus, integral subscript 0 superscript straight pi 4 cos squared open parentheses 5 x close parentheses d x equals 2 straight pi.

EXAMPLE

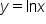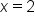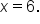Find the exact area of the region between the graphs of y equals ln x and the x-axis between x equals 2 and x equals 6. The region is in the figure below.

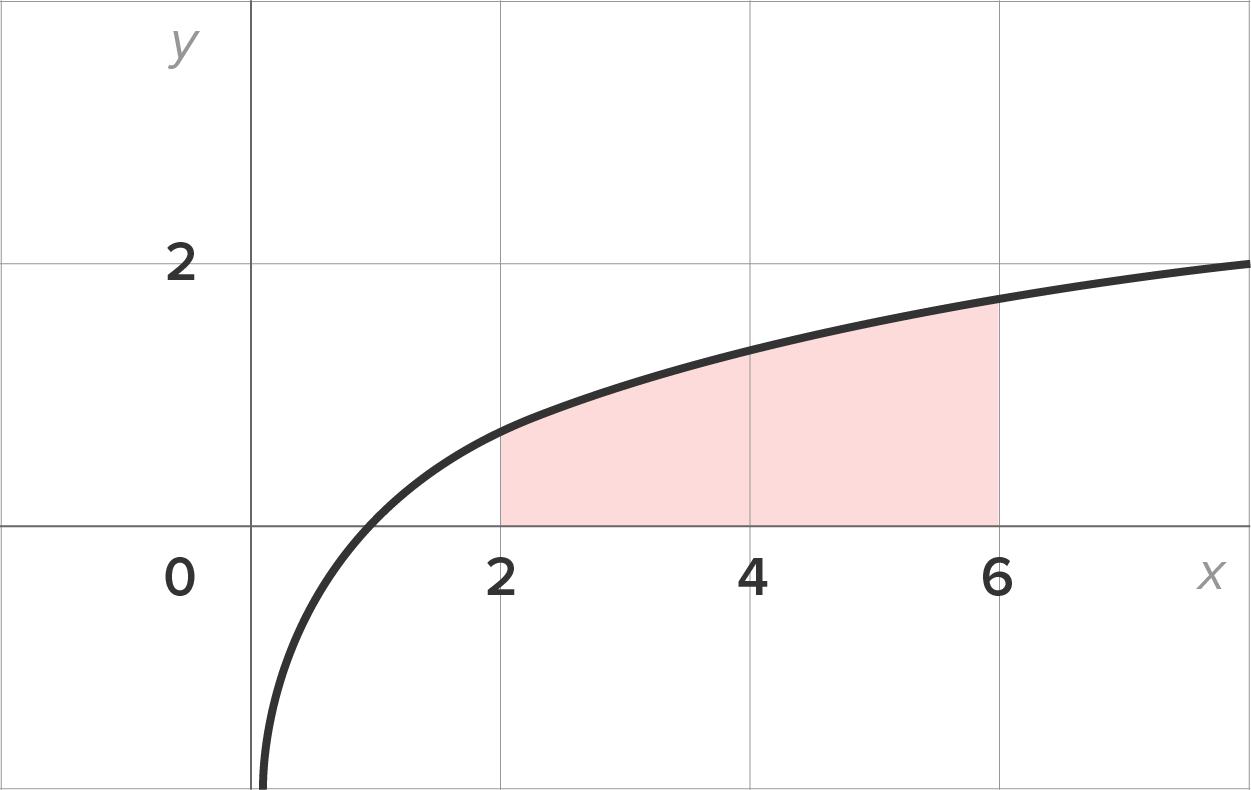
A graph with an x-axis ranging from 0 to 6 and a y-axis ranging from 0 to 2 at intervals of 2. A curve rises along the negative y-axis from the fourth quadrant to the first quadrant by passing through the points (1, 0), (2, 0.5), (4, 1.2), and (6, 1.8). The area below the curve up to the x-axis is shaded from x equals 2 to x equals 6.

Since the region is entirely above the x-axis on the interval open square brackets 2 comma space 6 close square brackets comma the area is given by the definite integral 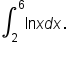integral subscript 2 superscript 6 ln x d x.

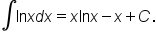Formula #37 in the table states that integral ln x d x equals x ln x minus x plus C. It follows that:

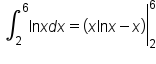
open integral subscript 2 superscript 6 ln x d x equals open parentheses x ln x minus x close parentheses close vertical bar subscript 2 superscript 6
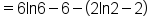
equals 6 ln 6 minus 6 minus open parentheses 2 ln 2 minus 2 close parentheses
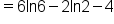
equals 6 ln 6 minus 2 ln 2 minus 4

try it
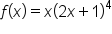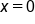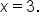
Consider the region bounded by the graphs of f open parentheses x close parentheses equals x open parentheses 2 x plus 1 close parentheses to the power of 4 and the x-axis between x equals 0 and x equals 3.
Set up and evaluate a definite integral that gives the area of the described region.
Since the graph of f open parentheses x close parentheses equals x open parentheses 2 x plus 1 close parentheses to the power of 4 is above the x-axis on the interval open square brackets 0 comma space 3 close square brackets comma the definite integral used to compute the area is integral subscript 0 superscript 3 x open parentheses 2 x plus 1 close parentheses to the power of 4 d x.

This integral resembles formula #9 from the table, which states:

integral x open parentheses a x plus b close parentheses to the power of n d x equals 1 over a squared open parentheses a x plus b close parentheses to the power of n plus 1 end exponent open square brackets fraction numerator a x plus b over denominator n plus 2 end fraction minus fraction numerator b over denominator n plus 1 end fraction close square brackets plus C comma space n not equal to short dash 1 comma short dash 2

For our integral, a equals 2 comma b equals 1 comma and n equals 4 comma which means:

integral x open parentheses 2 x plus 1 close parentheses to the power of 4 d x equals 1 over 2 squared open parentheses 2 x plus 1 close parentheses to the power of 4 plus 1 end exponent open square brackets fraction numerator 2 x plus 1 over denominator 4 plus 2 end fraction minus fraction numerator 1 over denominator 4 plus 1 end fraction close square brackets plus C

Or in simpler form:

integral x open parentheses 2 x plus 1 close parentheses to the power of 4 d x equals 1 fourth open parentheses 2 x plus 1 close parentheses to the power of 5 open parentheses fraction numerator 2 x plus 1 over denominator 6 end fraction minus 1 fifth close parentheses plus C

Then, the value of the definite integral is:

open 1 fourth open parentheses 2 x plus 1 close parentheses to the power of 5 open parentheses fraction numerator 2 x plus 1 over denominator 6 end fraction minus 1 fifth close parentheses close vertical bar subscript 0 superscript 3

Substituting x equals 3 and x equals 0 comma then subtracting, we have:

1 fourth open parentheses 2 open parentheses 3 close parentheses plus 1 close parentheses to the power of 5 open parentheses fraction numerator 2 open parentheses 3 close parentheses plus 1 over denominator 6 end fraction minus 1 fifth close parentheses minus 1 fourth open parentheses 2 open parentheses 0 close parentheses plus 1 close parentheses to the power of 5 open parentheses fraction numerator 2 open parentheses 0 close parentheses plus 1 over denominator 6 end fraction minus 1 fifth close parentheses
equals 1 fourth open parentheses 7 close parentheses to the power of 5 open parentheses 7 over 6 minus 1 fifth close parentheses minus 1 fourth open parentheses 1 close parentheses to the power of 5 open parentheses 1 over 6 minus 1 fifth close parentheses
equals fraction numerator 243 comma 701 over denominator 60 end fraction space square space units

This is approximately 4061.68 square units.

summary
In this lesson, you learned how to use a table to find antiderivatives, as well as to solve applications involving definite integrals. Having a table of integrals is a great tool when solving problems in which antiderivatives are required, but as you can tell, these would be very difficult (and not realistic) to memorize. Through more study of antiderivatives, you can learn the techniques that are required to arrive at these antiderivatives.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 4 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.