Two-Step Linear Equations

1. Solving a Two-Step Linear Equation

This lesson builds upon what we learned earlier about using inverse operations to isolate the variable, applying this knowledge to equations requiring two steps to solve for the unknown value. Remember, when solving an equation for a variable, our main goal is to isolate a variable. In other words, we want to get the variable by itself on one side of the equation, with all other expressions on the other side of the equals sign. In this process, we must always remember that if we perform an operation on one side of the equation, we must do the same on the other side of the equal sign. Let's look at an example:

EXAMPLE

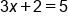
	Solve for x.
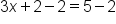
	You could divide every value by 3 or subtract 2 from both sides. If you divide everything by 3 first, you'll end up with fractions (or decimals), which would make it more challenging for the next step. Let's take the easiest option and subtract 2 from both sides.
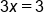
	This is the result after subtracting 2 from both sides.
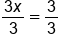
	Divide both sides by 3.
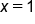
	Our Solution

hint

To solve a two-step equation, first move the constants (numbers that don’t have variables) to one side of the equation, then isolate the variable by canceling out the coefficient (numbers multiplied or divided by the variable).

EXAMPLE

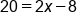
	Solve for x.
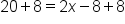
	Again, let's get rid of the value not touching the variable. So, add 8 to both sides because it is the opposite of subtraction.
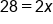
	This is the result after adding 8 to both sides.
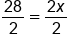
	Divide both sides by 2 because it is the opposite of multiplication.
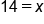
	Our Solution

big idea

Whatever we do on one side of the equation has to be done on the other side of the equation. This is known as the Rule of Equality.

try it

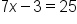
	Solve for x.
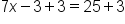
	We cancel the constant first on the side with the variable. Add 3 to both sides of the equation because it is the opposite of subtraction.
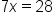
	This is the result after adding 3 to both sides.
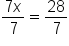
	Divide both sides of the equation by 7 because it is the opposite of multiplication.
	Our Solution

try it

	Solve for x.
	Subtract 5 from both sides because it is the opposite of addition.
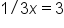
	This is the result after subtracting 5 from both sides.
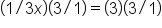
	Multiply both sides by 3/1. Why? Well, x is multiplied by 1/3. To isolate the variable, we would divide by 1/3. This is the same as multiplying both sides by the reciprocal 3/1, or 3.
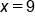
	Our Solution

IN CONTEXT

When working with word problems, it is always a good idea to start by clearly labeling the variables in a short list before we begin to solve the problem. This is important in all word problems involving variables, not just consecutive numbers or geometry problems. This is shown in the following example:

Speedy Taxi company charges $5 for the initial pick up and then $2/mile. If you spent $33, how many miles did you travel?



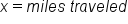
Now set up your equation.

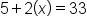
	Solve for x.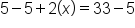
	Subtract 5 from both sides because it is the opposite of addition (or, in this case, a positive number).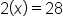
	This is the result after subtracting 5 from both sides.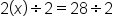
	Divide both sides by 2 because it is the opposite of multiplication.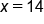
	Our Solution: You traveled 14 miles.

IN CONTEXT

A sofa and a loveseat together costs $444. The sofa costs double the loveseat. How much do they each cost?

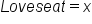
	With no information about the loveseat, this is our x.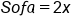
	Sofa is double the loveseat, so we multiply by 2.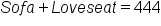
	Together, they cost $444, so we add them.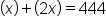
	Replace sofa and loveseat with labeled values.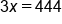
	Parentheses are not needed; combine like terms x and 2x.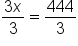
	Divide both sides by 3.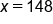
	Our solution for x.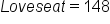
	Replace x with 148 in the original list.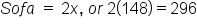
	The loveseat costs $148 and the sofa costs $296.

hint

Be careful of problems such as these. Many students see the phrase "double" and believe that it means we only have to divide 444 by 2 and get sofa equals 222 for one or both of the prices. As you can see, this will not work. By clearly labeling the variables in the original list, we know exactly how to set up and solve these problems.