Two-Sample Hypothesis Testing for Means: Two-Tailed Test

1. Introduction to Two-Sample Hypothesis Tests for Means

Transitioning from one-sample to two-sample hypothesis testing involves expanding your focus from analyzing a single group to comparing two distinct groups. In one-sample hypothesis testing, you assess whether the mean of a single sample significantly differs from a known or hypothesized population mean, denoted as 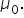This approach is useful when you have a specific benchmark or standard to compare against. However, in many real-world scenarios, you are interested in comparing the means of two independent groups to determine if there is a significant difference between them. This is where two-sample hypothesis testing comes into play. By comparing the means of two samples, you can draw conclusions about the differences between two populations. An example of this could be comparing the effectiveness of a marketing campaign for two different sales regions of the country.

1a. Types of Two-Sample Hypothesis Tests for Means

Just as there are three types of tests for one-sample hypothesis tests, there are similar tests for two-sample hypothesis tests, including two-tailed, right-tailed, and left-tailed tests.

In the table below, we'll look at each of these types of tests and provide an example of each.

Type of Test	Hypothesis	Example
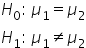
Two-Tailed		Comparing the average monthly expenses of the marketing and development departments to see if there is any difference.
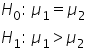
Right-Tailed		Comparing the average monthly sales of Store A to Store B to see if Store A has higher sales.
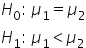
Left-Tailed		Comparing the average monthly expenses of marketing strategy A to see if it is less expensive compared to marketing strategy B.

try it

For each scenario state whether the test is a two-tailed, right-tailed, or left-tailed two-sample hypothesis test and state the hypotheses for the test.

1. A company wants to evaluate whether a new training program for customer service representatives has led to a decrease in the average response time to customer inquiries compared to the previous year.

This is a left-tailed test, and the hypotheses are:

(mean response time after the training program is the same as the mean response time before the training program)

(mean response time after the training program is less than the mean response time before the training program)

2. A company wants to compare the average number of tasks completed per day by employees in two different departments, Sales and Customer Support, to see if there is any difference in productivity.

This is a two-tailed test, and the hypotheses are:

(mean number of tasks completed per day by employees in Sales and Customer Support are equal)

(mean number of tasks completed per day by employees in Sales and Customer Support are different, not equal)

3. A retail company is comparing the average revenue generated by two different marketing campaigns, Campaign A and Campaign B, to determine if Campaign A generates more revenue than Campaign B.

This is a right-tailed test, and the hypotheses are:

(mean revenue generated by Campaign A is equal to the mean revenue generated by Campaign B)

(mean revenue generated by Campaign A is greater than the mean revenue generated by Campaign B)

1b. Steps in a Two-Sample Hypothesis Test for Means

Below are the steps you can use to perform a two-sample hypothesis test for means.

1. State the Hypotheses: Clearly define the null and alternative hypotheses.
2. Gather the Data: Gather data in a way that is designed to test the hypotheses.
3. Choose the Significance Level: Decide on the α level (for example, 0.05 or 0.10).
4. Check for Equal Variances: Before performing the t-test, check if the variances of the two groups are equal. Use an F-test to check if the variances of the two groups are equal.
5. Perform a Statistical Test: Use an appropriate statistical test to analyze the data. A two-sample t-test will be used.
6. Make a Decision: Based on the test results, decide whether to reject or fail to reject the null hypothesis. This decision is guided by a p-value, which indicates the probability of observing the data if the null hypothesis is true.
7. Interpret the Results: Explain the results of the hypothesis test in the context of the business problem.

2. Equal Variance Assumption in Two-Sample Hypothesis Tests for Means

When comparing the means of two groups using a t-test, it’s important to check if the variances (a measure of how spread out the data is) of the two groups are equal. This is known as the equal variance assumption.

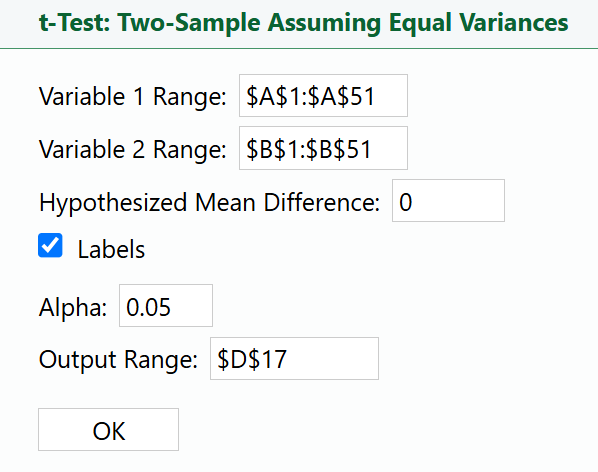
A t-test will be used to perform the two-sample hypothesis test for two means. The standard two-sample t-test assumes that the variances of the two groups are equal. If this assumption is not true, the test results might be inaccurate. This could lead to wrong conclusions about whether the means of the two groups are different.

If the variances are equal, you use the pooled t-test. This test combines the variances of both groups into one, making the calculation simpler. If the variances are not equal, you use Welch’s t-test. This test adjusts for the difference in variances, providing more reliable results when the spreads of the data are different.

Let’s look at how you would determine if you had equal variances or not among two groups of interest.

EXAMPLE

TechWave Innovations is a rapidly growing tech company specializing in developing cutting-edge software solutions. The company has two main departments: Marketing and Development. Recently, the CFO (Chief Financial Officer) has noticed fluctuations in the monthly expenses of these departments and wants to ensure that resources are being allocated efficiently.

The CFO has asked you to compare the average monthly expenses of the Marketing and Development departments to determine if there is a significant difference between them. The results of this hypothesis test will help in making informed budget allocation decisions for the upcoming fiscal year.

You realize that you will need to perform a two-sample t-test for means. If the variability in expenses is similar for both departments, you would use the t-test for equal variances. If one department has much more variability in expenses than the other, you would use the t-test for unequal variances.

By checking for equal variances, you ensure that you are using the correct method for your data, leading to more accurate and trustworthy results. This step is crucial for making informed business decisions based on your analysis.

You test the following in Excel.

• (variance in monthly expenses for the Marketing department is equal to the variance in monthly expenses for the Development department)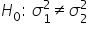
• (variance in monthly expenses for the Marketing department is not equal to the variance in monthly expenses for the Development department)

To perform the equality of variances test in Excel using the monthly_expense_comparison.xlsx file, perform the following:

1. Select F-Test Two Sample for Variances in the XL Miner Analysis Toolpak. The dialog box opens.



2. Place your cursor in the Variable 1 Range: box and select the data in column A.

3. Place your cursor in the Variable 2 Range: box and select the data in column B.

4. Place your cursor in the Output Range: box and select cell D3 in the Excel worksheet. Select OK.



You will obtain the following output in your Excel worksheet.



The value circled in column E11 is the probability that the F-statistic is less than or equal to the observed value under the null hypothesis for a one-tailed test. That is, it is the p-value for a one-tailed test.

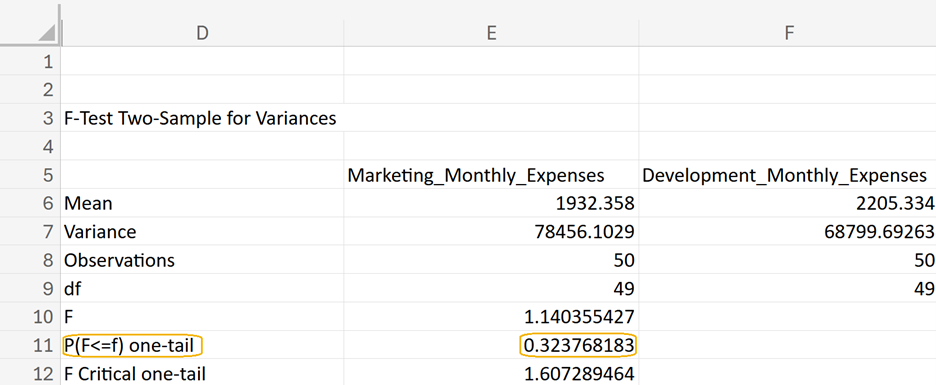
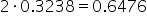To obtain the two-tailed p-value, you need to multiply the one-tail p-value by 2. So is the p-value for the hypothesis test for the equality of variances. With this p-value, using a level of significance (α) of 0.05, you fail to reject the null hypothesis.

This result means there is not enough evidence to conclude that the variances of the two groups are different. In other words, the variances are considered equal for the purposes of selecting the appropriate t-test.

When you perform the two-sample t-test for the means, you will select the t-test that assumes equal variances.

3. Two-Sample Hypothesis Testing for Means: Two-Tailed

In the upcoming sections, you will explore how to perform a two-tailed hypothesis test for detecting differences in means. You will discover the purpose of the test, how to perform the test, and how to interpret the results. Examples and hands-on exercises will illustrate how to set up and interpret a two-tailed test for testing the difference between two means, helping you understand when and how to use them. By working through these scenarios, you will gain a deeper insight into hypothesis testing for testing differences among the means from two populations and their applications in real-world data analysis.

3a. Applications of Two-Sample Hypothesis Tests for Means: Two-Tailed Tests

Let's walk through a practical example of performing a two-sample hypothesis test for means for a two-tailed test.

EXAMPLE

Continuing with the TechWave Innovations example from the previous section, conduct the two-sample t-test, now that you know you can assume equal variances among the Marketing and Development departments' expenses.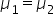

Step 1: State the Hypotheses

• H₀: (no difference in the average monthly expenses between the Marketing and Development departments)
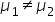• H₁: (there is a difference in the average monthly expenses between the Marketing and Development departments)

Step 2: Gather the Data

The business data analytics team collects monthly expense data for the past year from both departments, resulting in 50 observations for each department.

Step 3: Choose a Significance Level

Use a level of significance,

Step 4: Check for Equal Variances

You have already performed the equality of variances hypothesis test in the last section and concluded that the variances for the two groups of expenses among the Marketing and Development departments are considered to be equal.

Step 5: Perform a Statistical Test

You will now use the XL Miner Analysis Toolpak to find the p-value for this two-sample hypothesis test (two-tailed) using the data in the monthly_expense_comparison.xlsx Excel file.

1. Select t-Test: Two-Sample Assuming Equal Variance in the XL Miner Analysis Toolpak. The dialog box opens.



2. Place your cursor in the Variable 1 Range: box and select the data in column A.

3. Place your cursor in the Variable 2 Range: box and select the data in column B.

4. Enter 0 in the Hypothesized Mean Difference: box.

5. Place your cursor in the Output Range: box and select cell D16 in the Excel worksheet. Select OK.



You will obtain the following output in your Excel worksheet.



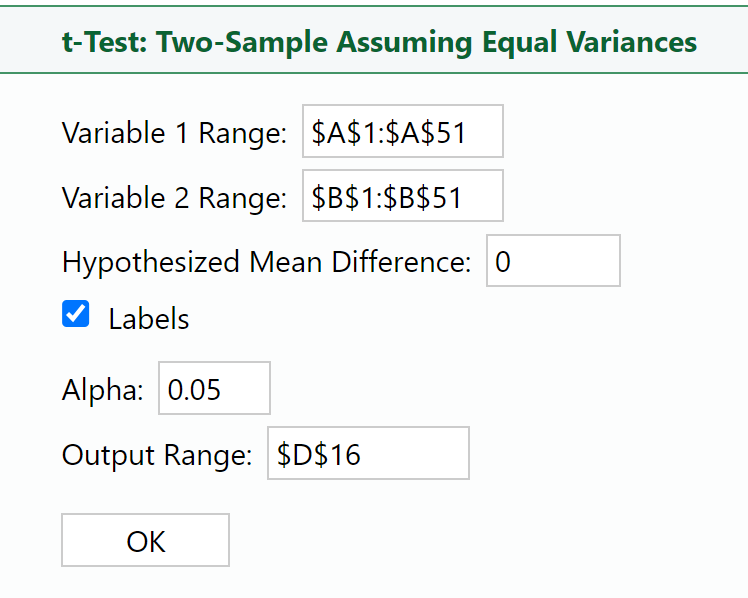
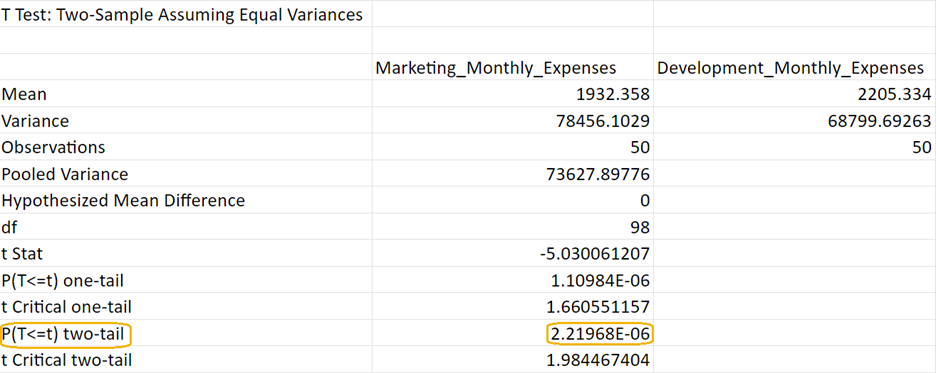
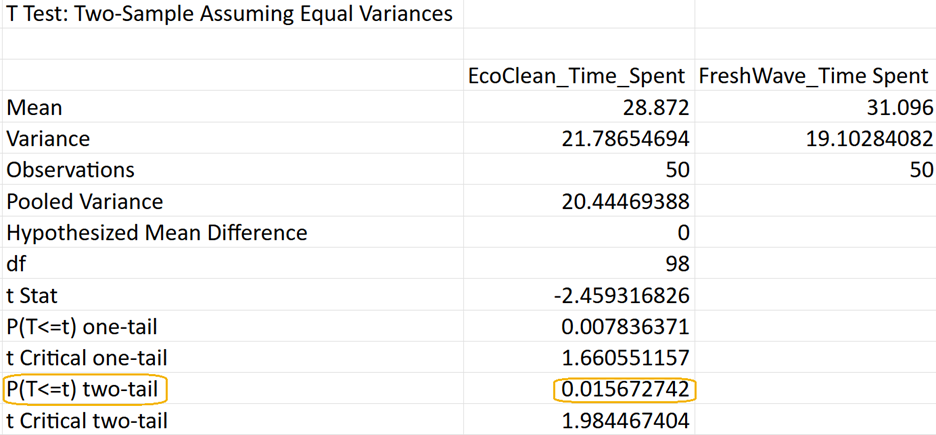
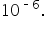In the output, find the row labeled P(T<=t) two-tail. This row contains the two-tailed p-value. In this case, the p-value is 2.21968E-06. This number is in scientific notation. 2.21968 is the coefficient and E-06 means the coefficient needs to be multiplied by To convert 2.21968E-06 to standard form, multiply 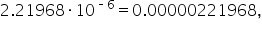which is a very small p-value!

Step 6: Make a Decision

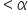Since the p-value (level of significance), you reject the null hypothesis.

Step 7: Interpret the Results

Since the p-value is less than the significance level (0.05), you reject the null hypothesis. There is a statistically significant difference between the average monthly expenses of the Marketing and Development departments at TechWave Innovations.

The significant difference in expenses suggests that the two departments manage their budgets differently. This information can be crucial for the CFO and management team when making decisions about budget allocations, cost control measures, and financial planning.

The company might investigate further to understand why the expenses differ and whether any adjustments are needed to optimize spending and resource allocation.

try it

For the scenario provided, construct a two-sample t-test to address the business problem. Use a level of significance of 0.05. Ensure your solution contains:

1. A statement of the hypotheses.
2. A test for equality of variances.
3. An interpretation of what the result of the hypothesis test means in the context of the problem.

A leading consumer goods company, GreenWave Inc., has recently launched two new eco-friendly detergent products: EcoClean Detergent and FreshWave Detergent. Both products are marketed as environmentally friendly and effective cleaning solutions, but they target slightly different customer segments. EcoClean is promoted as a budget-friendly option, while FreshWave is positioned as a premium product with additional fragrance options.

The marketing team at GreenWave Inc. wants to understand how potential customers engage with the product pages for EcoClean and FreshWave on their website. Specifically, they are interested in comparing the average time spent on each product’s webpage to determine if there are any significant differences in user engagement.

You have been tasked with performing a two-sample t-test to determine if there is a significant difference in the average time spent on each product’s webpage.

Solution:

Before you conduct the hypothesis test, you need to determine whether the variability in the time spent on the website for each product is similar or not. Conduct an equality of variances test in Excel and interpret the results. Use a level of significance of 0.05. The Excel file detergent_time_website.xlsx contains the data.

The hypotheses are:

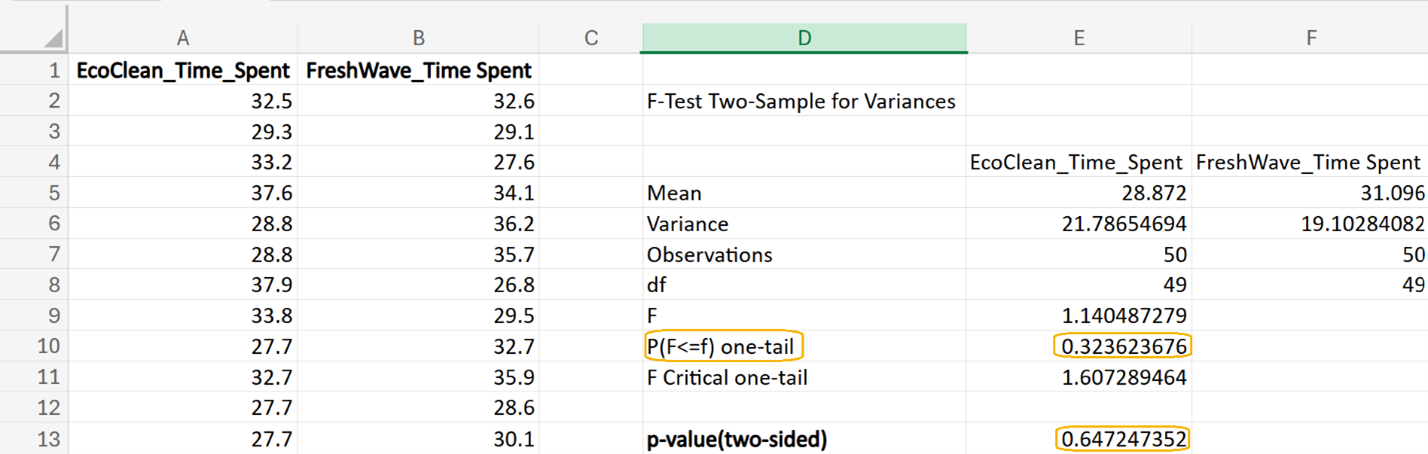
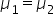• H₀: (mean amount of time spent on EcoClean product page is the same as mean amount of time spend on FreshWave product page for all visitors)
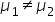• H₁: (mean amount of time spent on EcoClean product page is not the same as mean amount of time spent on FreshWave product page for all visitors)

You need to perform the equality of variances test to determine which t-test you will select for the two-sample hypothesis test.

The hypotheses are:

• 
• 

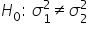
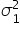is population variance for EcoClean and measures how much the time spent on the EcoClean product page varies among all visitors. 

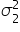is the population variance for FreshWave and measures how much the time spent on the FreshWave product page varies among all visitors. 

Use the F-Test Two-Sample for Variances option in the XL Miner Analysis Toolpak. Your options should look like:



From Excel, you obtain the following output. In cell E13, you can enter =2*E10 to obtain the 2-sided p-value for this test. With this p-value, using a level of significance (α) of 0.05, you fail to reject the null hypothesis.

This result means there is not enough evidence to conclude that the variances of the time spent on the EcoClean and FreshWave product pages are different. In other words, the variances are considered equal for the purposes of selecting the appropriate two-sample t-test.



For the two-sample hypothesis test, you will select the t-Test: Two-Sample Assuming Equal Variances option in XL Miner.



You obtain the following output from Excel. In the output, find the row labeled P(T<=t) two-tail. This row contains the two-tailed p-value. The p-value for this two-sample hypothesis test is 0.0157.



Since the p-value (0.0157) is less than the significance level (0.05), you reject the null hypothesis. This result means there is enough evidence to conclude that there is a statistically significant difference in the average time spent on the EcoClean and FreshWave product pages for all customers.

watch

Follow along with this video on conducting a two-sample t-test to analyze the average time spent on webpages.