Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Transformations of Graphs of Logarithmic Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will apply transformations to graphs of logarithmic functions and determine properties of transformed logarithmic functions. Specifically, this lesson will cover:

Table of Contents

1. Applying Transformations to Graphs of Logarithmic Functions

Throughout this course, we have applied several different translations to a function and observed the transformations of the corresponding graph. When applying these translations to logarithmic functions, we will also observe how the properties of a logarithmic function are affected.

EXAMPLE

Consider the function g open parentheses x close parentheses equals 2 plus log subscript 4 open parentheses x minus 5 close parentheses.

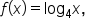Compared to the graph of f open parentheses x close parentheses equals log subscript 4 x comma we know the following:

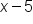  • The “x minus 5” tells us that the graph is shifted 5 units to the right.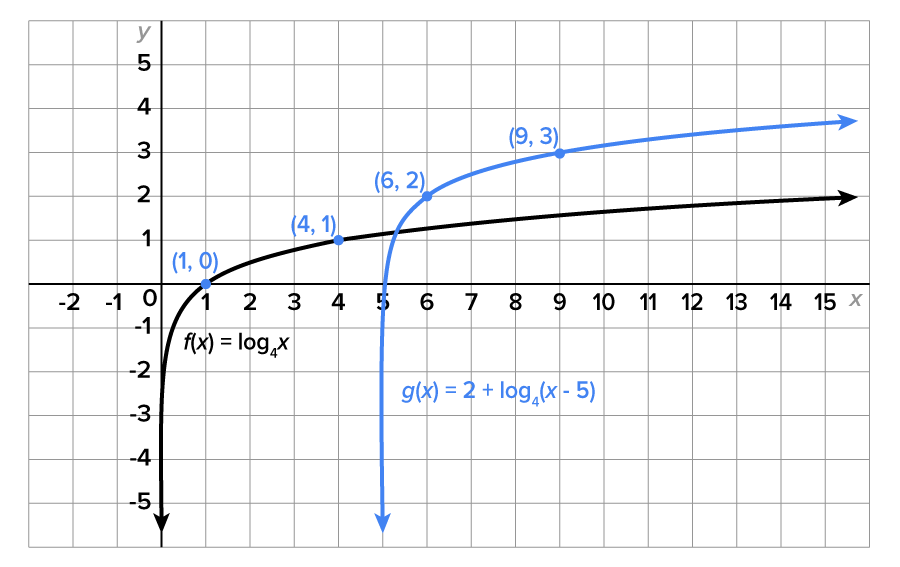
  • The constant term tells us that the graph is also shifted up 2 units.
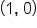Here are the graphs of f and g on the same axes:



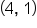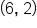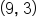Since the graph of f moves to the right 5 units and up 2 units, note that the points open parentheses 1 comma space 0 close parentheses and open parentheses 4 comma space 1 close parentheses on the graph of f correspond to the points open parentheses 6 comma space 2 close parentheses and open parentheses 9 comma space 3 close parentheses on the graph of g, respectively.

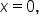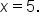
Note that since the graph of f shifts 5 units to the right, the vertical asymptote also shifts 5 units to the right. In other words, the vertical asymptote of g open parentheses x close parentheses is 5 units to the right of x equals 0 comma which is x equals 5.

try it
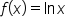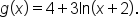
Consider the functions f open parentheses x close parentheses equals ln     x and g open parentheses x close parentheses equals 4 plus 3 ln   open parentheses x plus 2 close parentheses.
List the sequence of transformations that are applied to the graph of f in order to obtain the graph of g.
The graph of f is moved 2 units to the left, stretched vertically by a factor of 3, and moved upward 4 units.

Now that we have applied transformations to some logarithmic functions, let’s see how these transformations affect the properties of logarithmic functions.

2. Properties of Graphs of Transformed Logarithmic Functions

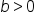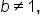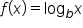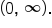
If b greater than 0 and b not equal to 1 comma recall that the domain of f open parentheses x close parentheses equals log subscript b x is open parentheses 0 comma space infinity close parentheses.

In other words, logarithms can only be applied to positive numbers, meaning that the argument of a logarithmic function must be positive.

Now consider the function 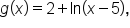g open parentheses x close parentheses equals 2 plus ln   open parentheses x minus 5 close parentheses comma which we graphed earlier. Since the argument of this function is 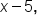x minus 5 comma the domain is the set of numbers for which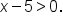 x minus 5 greater than 0.

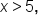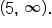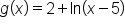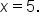
Solving for x gives x greater than 5 comma or using interval notation, open parentheses 5 comma space infinity close parentheses. Recall also that the vertical asymptote of g open parentheses x close parentheses equals 2 plus ln   open parentheses x minus 5 close parentheses is x equals 5.

In general, shifting a logarithmic function horizontally will have an effect on the domain of the function as well as the vertical asymptote. Notice that they are related.

big idea
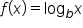The domain of a logarithmic function f open parentheses x close parentheses equals log subscript b x is the set of values for which the argument, x, is positive. The vertical asymptote of f is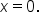 x equals 0.

When there is a more complicated argument, the domain of the function is the set of all values of x for which the argument is positive.

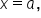If the argument is equal to zero when x equals a comma then the vertical asymptote of the function is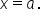 x equals a.

Since the range of a logarithmic function is the set of real numbers, vertical and horizontal translations and stretches do not alter the range of a logarithmic function. That is, the range of a transformed logarithmic function is also open parentheses short dash infinity comma space infinity close parentheses.

EXAMPLE

Determine the domain, range, and vertical asymptote of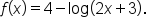 f open parentheses x close parentheses equals 4 minus log   open parentheses 2 x plus 3 close parentheses.

The domain is the set of all numbers for which the argument is positive.

2 x plus 3 greater than 0 Set the argument greater than 0.
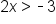2 x greater than short dash 3
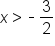
x greater than short dash 3 over 2 		Solve the inequality for x.
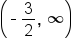
open parentheses short dash 3 over 2 comma space infinity close parentheses Write using interval notation.

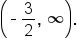
Thus, the domain of f is open parentheses short dash 3 over 2 comma space infinity close parentheses.

The range is the set of real numbers, written open parentheses short dash infinity comma space infinity close parentheses.

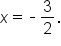
The vertical asymptote is x equals short dash 3 over 2.

try it
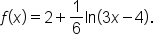
Consider the function f open parentheses x close parentheses equals 2 plus 1 over 6 ln   open parentheses 3 x minus 4 close parentheses.
Determine the domain, range, and vertical asymptote of f.
The domain of a logarithmic function is the set of all values for which the argument of the logarithm is positive:

3 x minus 4 greater than 0 space space space space space space space 3 x greater than 4 space space space space space space space space space space x greater than 4 over 3

Expressed using interval notation, the domain is open parentheses 4 over 3 comma space infinity close parentheses.

The range of a logarithmic function is open parentheses short dash infinity comma space infinity close parentheses.

The vertical asymptote corresponds to the value(s) of x for which the argument is equal to 0.

3 x minus 4 equals 0 space space space space space space space 3 x equals 4 space space space space space space space space space space x equals 4 over 3

The vertical asymptote has equation x equals 4 over 3.

summary
In this lesson, you learned that when applying transformations to graphs of logarithmic functions, the properties of the original function change according to the horizontal translations. You also learned about the properties of graphs of transformed logarithmic functions, noting that in general, shifting a logarithmic function horizontally will have an effect on the domain of the function as well as the vertical asymptote. 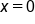More specifically, if a horizontal translation was applied to a logarithmic function, the vertical asymptote shifts away from x equals 0 and the domain shifts from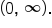 open parentheses 0 comma space infinity close parentheses.

SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.