Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Transformations of Graphs of Exponential Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will use transformations to graph exponential functions and examine their properties. Specifically, this lesson will cover:

Table of Contents

1. Horizontal Translations of Exponential Functions

Given the graph of 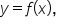y equals f open parentheses x close parentheses comma recall the following for a positive value of k  :

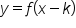  • The graph of y equals f open parentheses x minus k close parentheses shifts the graph of f open parentheses x close parentheses to the right k units.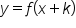
  • The graph of y equals f open parentheses x plus k close parentheses shifts the graph of f open parentheses x close parentheses to the left k units.

EXAMPLE

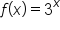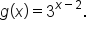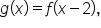Consider the functions f open parentheses x close parentheses equals 3 to the power of x and g open parentheses x close parentheses equals 3 to the power of x minus 2 end exponent. Since g open parentheses x close parentheses equals f open parentheses x minus 2 close parentheses comma it follows that the graph of g open parentheses x close parentheses is obtained by shifting the graph of f open parentheses x close parentheses to the right by 2 units. Their graphs are shown below.

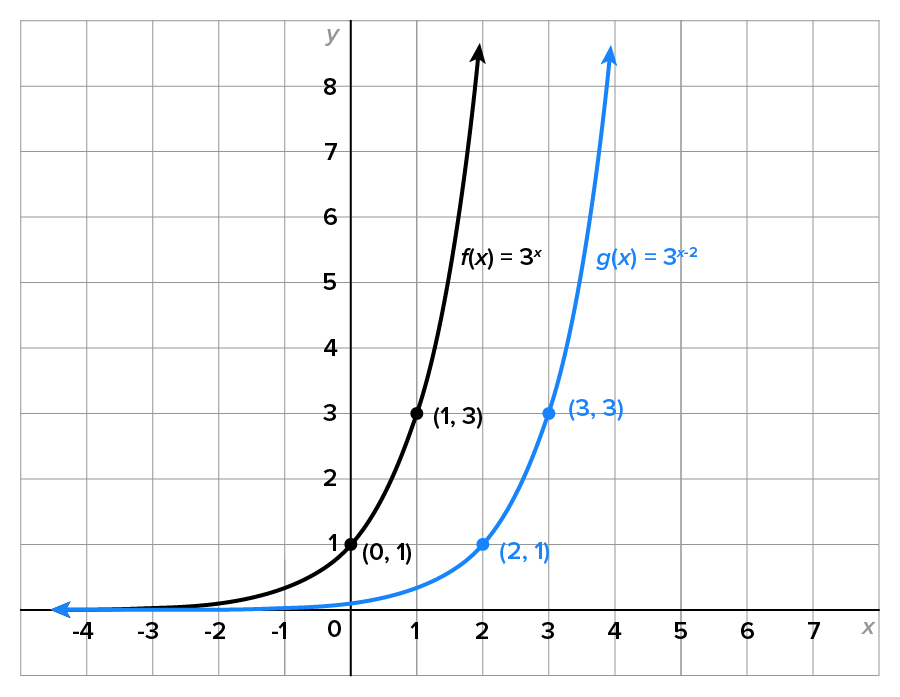
A graph with an x-axis ranging from −4 to 7 and a y-axis ranging from 0 to 8. The graph has two curves, where one curve with the equation f of x equals 3 to the power x rises from the upper left quadrant, along the negative x-axis, passes through the marked points at (0, 1) and (1, 3), and extends upward into the upper right quadrant. The other curve with the equation g of x equals 3 raised to the power x – 2 rises from the upper left quadrant, along the negative x-axis, passes through the marked points at (2, 1) and (3, 3), and extends upward into the upper right quadrant.

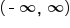The domain of f is open parentheses short dash infinity comma space infinity close parentheses and the range of f is 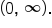open parentheses 0 comma space infinity close parentheses. It turns out that the domain of g is 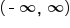open parentheses short dash infinity comma space infinity close parentheses and the range of g is 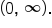open parentheses 0 comma space infinity close parentheses. In general, shifting the graph of a function horizontally does not alter the domain or range of f.

try it
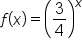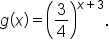
Consider the functions f open parentheses x close parentheses equals open parentheses 3 over 4 close parentheses to the power of x and g open parentheses x close parentheses equals open parentheses 3 over 4 close parentheses to the power of x plus 3 end exponent.
Explain how the graph of g is related to the graph of f.
The graph of g is obtained by shifting the graph of f to the left 3 units.

2. Vertical Translations of Exponential Functions

Given the graph of 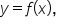y equals f open parentheses x close parentheses comma recall the following for a positive value of k  :

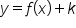  • The graph of y equals f open parentheses x close parentheses plus k shifts the graph of f open parentheses x close parentheses up k units.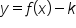
  • The graph of y equals f open parentheses x close parentheses minus k shifts the graph of f open parentheses x close parentheses down k units.

EXAMPLE

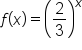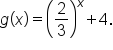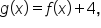Consider the functions f open parentheses x close parentheses equals open parentheses 2 over 3 close parentheses to the power of x and g open parentheses x close parentheses equals open parentheses 2 over 3 close parentheses to the power of x plus 4. Since g open parentheses x close parentheses equals f open parentheses x close parentheses plus 4 comma it follows that the graph of g open parentheses x close parentheses is obtained by shifting the graph of f open parentheses x close parentheses up 4 units. Their graphs are shown below.

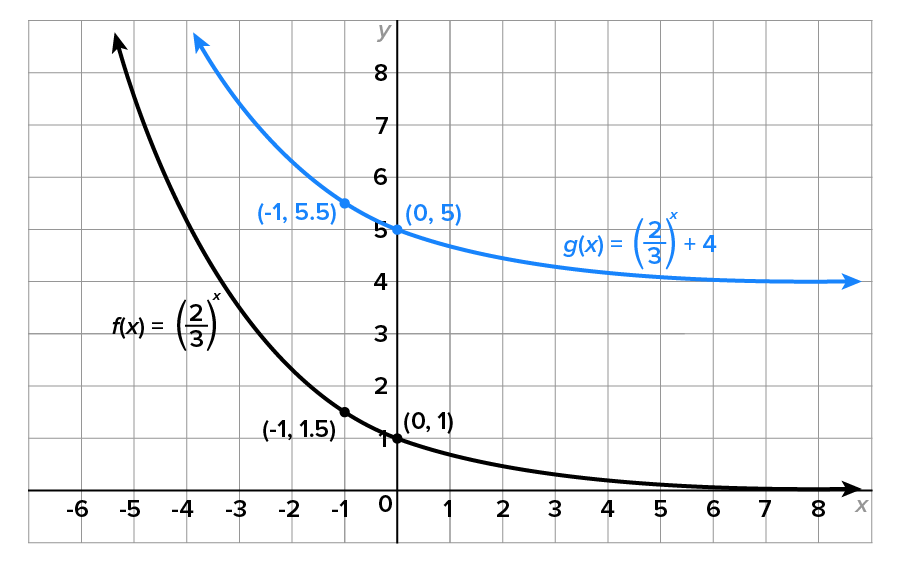
A graph with an x-axis ranging from −6 to 8 and a y-axis ranging from 0 to 8. The graph has two curves, where one curve with the equation f of x equals (2 over 3)x descends from the upper left quadrant, opens upward, passes through the marked points at (−1, 1.5) and (0, 1), and extends into the upper right quadrant along the x-axis. The other curve with the equation g of x equals (2 over 3) to the power x plus 4 descends from the upper left quadrant, opens upward, passes through the marked points at (−1, 5.5) and (0, 5), and extends into the upper right quadrant beyond the point (8, 4).

The domains of both f and g are open parentheses short dash infinity comma space infinity close parentheses. However, take a closer look at the ranges of f and g  :

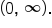
  • The range of f is open parentheses 0 comma space infinity close parentheses.
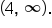
  • The range of g is open parentheses 4 comma space infinity close parentheses.
When the graph shifts vertically, the range is shifted as well.

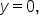Notice also that the horizontal asymptote of f is y equals 0 comma while the horizontal asymptote of g is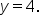 y equals 4.

big idea
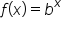When the graph of the exponential function f open parentheses x close parentheses equals b to the power of x is shifted up k units, its range becomes 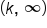open parentheses k comma space infinity close parentheses and the horizontal asymptote becomes y equals k.

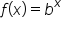When the graph of the exponential function f open parentheses x close parentheses equals b to the power of x is shifted down k units, its range becomes 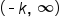open parentheses short dash k comma space infinity close parentheses and the horizontal asymptote becomes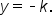 y equals short dash k.

try it
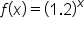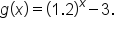
Consider the functions f open parentheses x close parentheses equals open parentheses 1.2 close parentheses to the power of x and g open parentheses x close parentheses equals open parentheses 1.2 close parentheses to the power of x minus 3.
Explain how the graph of g is related to the graph of f.
The graph of g is obtained by shifting the graph of f down 3 units.
What is the range of g  ?
The range is open parentheses short dash 3 comma space infinity close parentheses.
What is the equation of the horizontal asymptote of g  ?
The equation is y equals short dash 3.

3. Vertical Compressions and Stretches of Exponential Functions

Given the graph of 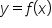y equals f open parentheses x close parentheses and a positive number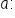 a colon

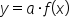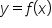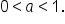
  • The graph of y equals a times f open parentheses x close parentheses is vertical compression of the graph of y equals f open parentheses x close parentheses if 0 less than a less than 1.
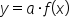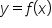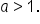
  • The graph of y equals a times f open parentheses x close parentheses is a vertical stretch of the graph of y equals f open parentheses x close parentheses if a greater than 1.

EXAMPLE

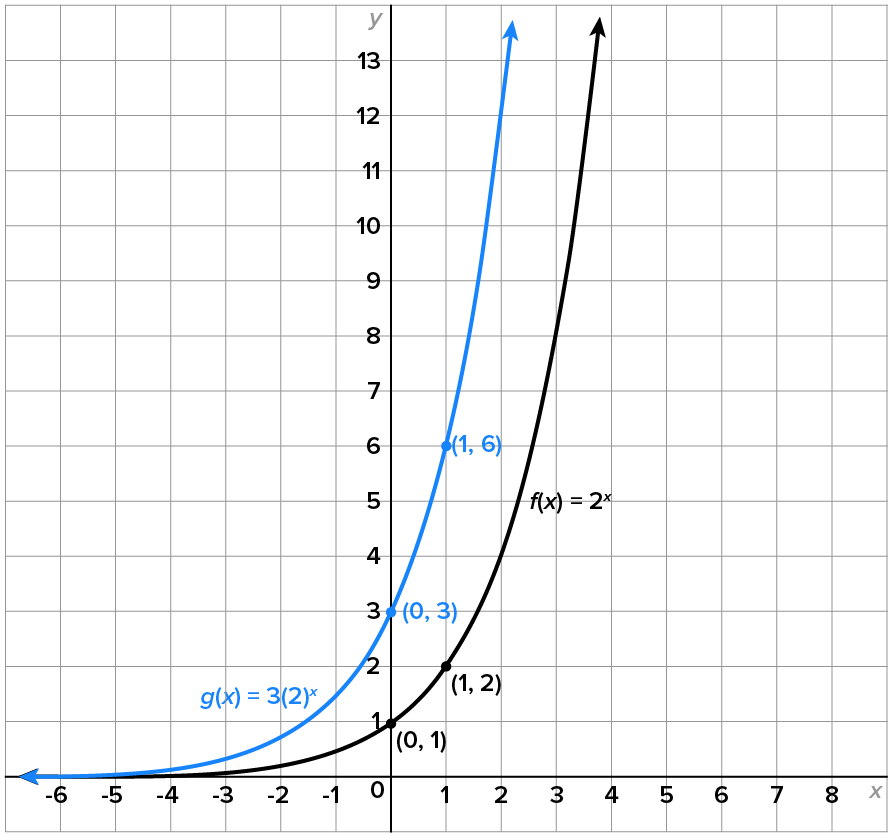
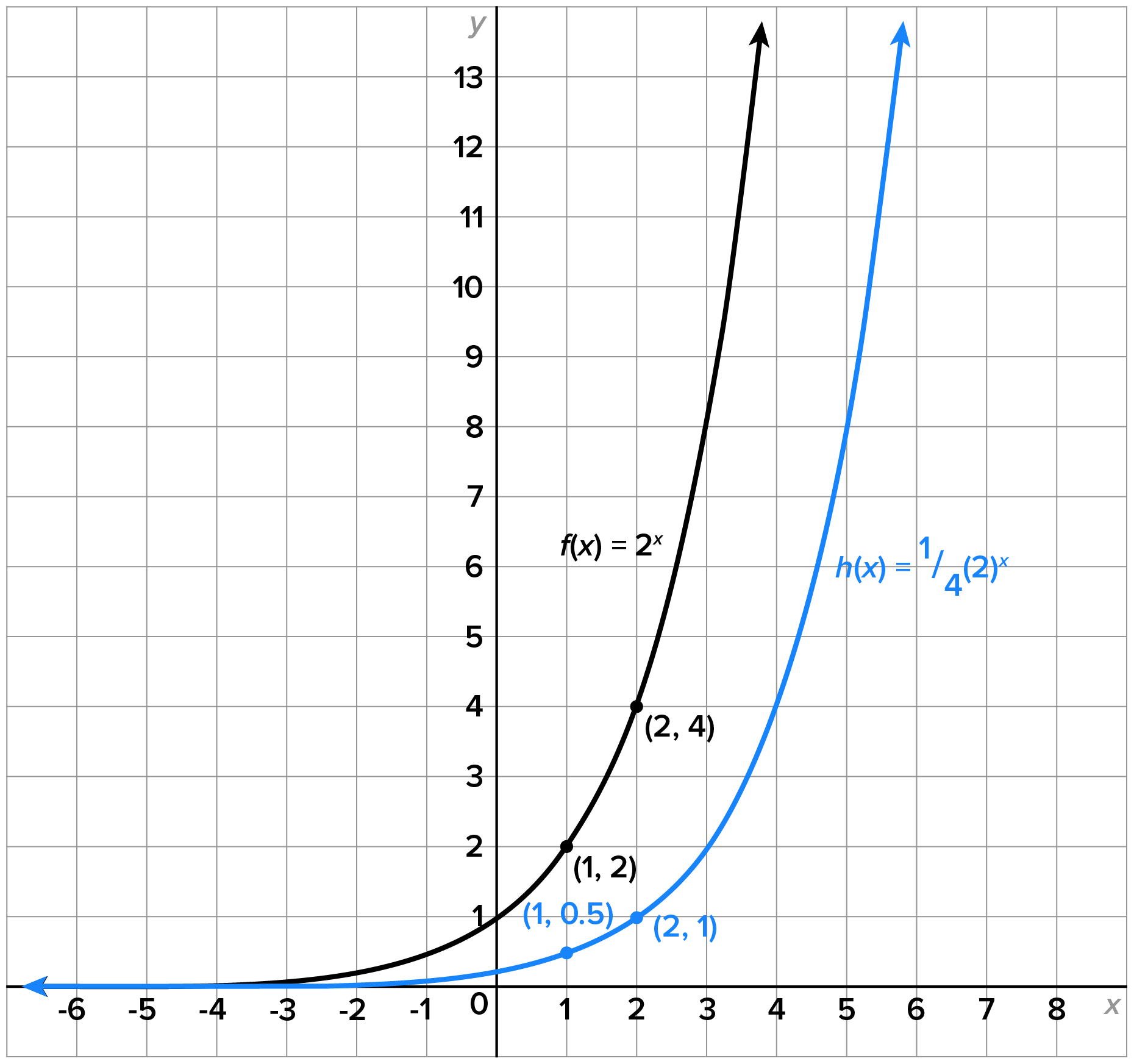
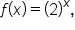
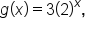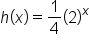Consider the functions f open parentheses x close parentheses equals open parentheses 2 close parentheses to the power of x comma g open parentheses x close parentheses equals 3 open parentheses 2 close parentheses to the power of x comma and h open parentheses x close parentheses equals 1 fourth open parentheses 2 close parentheses to the power of x. Notice that functions g and h are constant multiples of function f. The graphs of g and h are each shown with the graph of f below.

bold italic g open parentheses bold x close parentheses bold equals bold 3 open parentheses bold 2 close parentheses to the power of bold x bold italic h open parentheses bold x close parentheses bold equals bold 1 over bold 4 open parentheses bold 2 close parentheses to the power of bold x
A graph with an x-axis ranging from −6 to 8 and a y-axis ranging from 0 to 13. The graph has two curves, where one curve with the equation f of x equals 2 tp the power x rises from the upper left quadrant, along the negative x-axis, passes through the marked points at (0, 1) and (1, 2), and extends upward into the upper right quadrant. The other curve with the equation g of x equals 3(2) to the power x rises from the upper left quadrant, along the negative x-axis, passes through the marked points at (0, 3) and (1, 6), and extends upward into the upper right quadrant. A graph with an x-axis ranging from −6 to 8 and a y-axis ranging from 0 to 13. The graph has two curves, where one curve with the equation f of x equals 2 to the power x rises from the upper left quadrant, along the negative x-axis, passes through the marked points at (1, 2) and (2, 4), and extends upward into the upper right quadrant. The other curve with the equation h(x) equals (1 over 4)(2) to the power x rises from the upper left quadrant, along the negative x-axis, passes through the marked points at (1, 0.5) and (2, 1), and extends upward into the upper right quadrant.

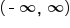The functions f, g, and h all have domain open parentheses short dash infinity comma space infinity close parentheses and range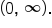 open parentheses 0 comma space infinity close parentheses.

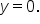
Also, each function has horizontal asymptote y equals 0.

4. Reflections of Exponential Functions

Given the graph of 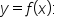y equals f open parentheses x close parentheses colon

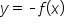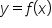  • The graph of y equals short dash f open parentheses x close parentheses is the reflection of the graph of y equals f open parentheses x close parentheses across the x-axis.
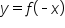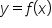  • The graph of y equals f open parentheses short dash x close parentheses is the reflection of the graph of y equals f open parentheses x close parentheses across the y-axis.

EXAMPLE

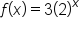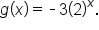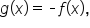Consider the functions f open parentheses x close parentheses equals 3 open parentheses 2 close parentheses to the power of x and g open parentheses x close parentheses equals short dash 3 open parentheses 2 close parentheses to the power of x. Since g open parentheses x close parentheses equals short dash f open parentheses x close parentheses comma it follows that the graph of g open parentheses x close parentheses is obtained by reflecting the graph of f open parentheses x close parentheses around the x-axis. Their graphs are shown below.

A graph with an x-axis ranging from −8 to 6 and a y-axis ranging from −7 to 7. The graph has two curves, where one curve with the equation f of x equals 3(2) to the power x rises from the upper left quadrant, along the negative x-axis, passes through the marked points at (−1, 1.5) and (0, 3), and extends upward into the upper right quadrant. The other curve with the equation g of x equals -3(2) to the power x descends from the lower left quadrant, along the negative x-axis, passes through the marked points at (−1, −1.5) and (0, −3), and extends downward into the lower right quadrant.

The domains of both f and g are open parentheses short dash infinity comma space infinity close parentheses. However, take a closer look at the ranges of f and g:

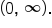
  • The range of f is open parentheses 0 comma space infinity close parentheses.
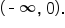
  • The range of g is open parentheses short dash infinity comma space 0 close parentheses.
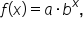Note: since these functions both have the form f open parentheses x close parentheses equals a times b to the power of x comma the aspects of these functions were discussed earlier.

Here is an example which illustrates a reflection across the y-axis.

EXAMPLE

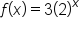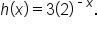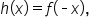Consider the functions f open parentheses x close parentheses equals 3 open parentheses 2 close parentheses to the power of x and h open parentheses x close parentheses equals 3 open parentheses 2 close parentheses to the power of short dash x end exponent. Since h open parentheses x close parentheses equals f open parentheses short dash x close parentheses comma it follows that the graph of 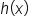h open parentheses x close parentheses is obtained by reflecting the graph of f open parentheses x close parentheses around the y-axis. Their graphs are shown below.

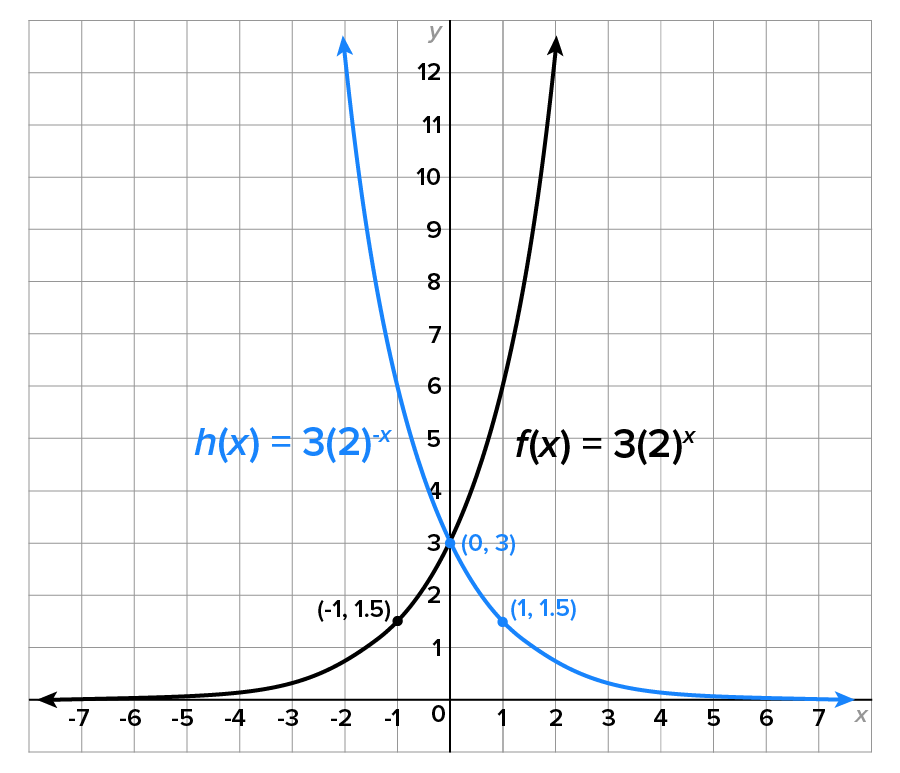
A graph with an x-axis ranging from −7 to 7 and a y-axis ranging from 0 to 12 in increments of 1. There are two curves, where the first curve is increasing, starts far to the left slightly above the x-axis. As x increases, the graph gets further from the axis, passes through the point (0, 3), then continues to curve upward into the upper right quadrant. The graph is labeled ‘f of x equals 3 times (2) to the power x’. The second curve descends rapidly from high in the upper left quadrant, passes through the points (-2, 12), (-1, 6), (0, 3), and (1, 1.5), then levels out as it approaches the x-axis. This graph is labeled ‘g of x equals 3 times (2) raised to the power (-x)’.

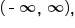The domains of both f and h are open parentheses short dash infinity comma space infinity close parentheses comma and the ranges of both f and h are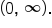 open parentheses 0 comma space infinity close parentheses.

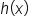Note: the equation for h open parentheses x close parentheses can be rewritten using properties of exponents:

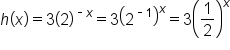
h open parentheses x close parentheses equals 3 open parentheses 2 close parentheses to the power of short dash x end exponent equals 3 open parentheses 2 to the power of short dash 1 end exponent close parentheses to the power of x equals 3 open parentheses 1 half close parentheses to the power of x

Thus, the equation of the exponential function obtained from reflecting across the y-axis has the same y-intercept, but its base is the reciprocal of the original base.

5. Combining Transformations

Similar to what we did earlier in the course, a series of transformations can be applied to one function to create another function.

EXAMPLE

Consider the function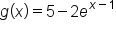 g open parentheses x close parentheses equals 5 minus 2 e to the power of x minus 1 end exponent in comparison with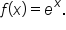 f open parentheses x close parentheses equals e to the power of x.

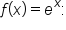
Notice the following transformations starting with the graph of f open parentheses x close parentheses equals e to the power of x colon

  • x was replaced with x minus 1 comma which shifts the graph of f to the right 1 unit.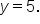
  • The “-2” multiplied to the exponential will cause the graph to reflect around the x-axis, as well as stretch vertically by a factor of 2.
  • The constant term “5” causes the graph to shift upward by 5 units. This also means that the horizontal asymptote is y equals 5.
The graphs of f and g are shown below:

A graph with an x-axis ranging from −9 to 5 and a y-axis ranging from −5 to 7. The graph has two curves, where one curve with the equation f of x equals e to the power x rises from the upper left quadrant, along the negative x-axis, passes through the marked point at (0, 1), and extends upward into the upper right quadrant. The other curve with the equation g of x equals 5 minus 2e to the power x minus 1 continues from the point (−9, 5) to (−2, 5) in the upper left quadrant and then extends downward into the lower right quadrant by passing between the points 4 and 5 on the y-axis and (2, 0) on the x-axis.

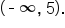
Note that the range of g is open parentheses short dash infinity comma space 5 close parentheses.

watch
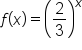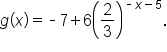
In this video, we describe the sequence of transformations that are applied to f open parentheses x close parentheses equals open parentheses 2 over 3 close parentheses to the power of x to obtain the graph g open parentheses x close parentheses equals short dash 7 plus 6 open parentheses 2 over 3 close parentheses to the power of short dash x minus 5 end exponent.

try it
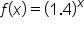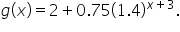
Consider the functions f open parentheses x close parentheses equals open parentheses 1.4 close parentheses to the power of x and g open parentheses x close parentheses equals 2 plus 0.75 open parentheses 1.4 close parentheses to the power of x plus 3 end exponent.
Describe the sequence of transformations that are applied to f to obtain the graph of g.
Since there is a coefficient of 0.75, the graph of f open parentheses x close parentheses gets vertically compressed by a factor of 0.75.

Since the exponent is x plus 3 instead of x, this means that the graph of f open parentheses x close parentheses will also shift 3 units to the left.

Since there is a constant 2 added to the function, this means that the graph of f open parentheses x close parentheses will shift upward 2 units.

These transformations can be applied to f to obtain the graph of g.

summary
In this lesson, you learned that exponential functions can undergo several transformations: horizontal and vertical translations, vertical compressions and stretches, and reflections around the x- and y-axes. Some transformations, such as vertical translations and reflections across the x-axis, produce a function with a different range than the original function. You also learned that you can combine transformations by applying a series of transformations to one function to create another function.

SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.