Theoretical Probability/A Priori Method

1. Theoretical Probability Model

A fairly common way to thinking about probability is to enumerate all the outcomes and assign them each an equal probability.

IN CONTEXT

When you roll a die, there are six results since they are numbered 1, 2, 3, 4, 5, or 6. Those are the outcomes.

Suppose you wanted to determine the probability of rolling a 2. Only one of those faces shows a 2, and there are six total faces, so the probability of you rolling a 2 is, therefore, one out of six.



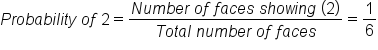
The understanding here is that the faces—1, 2, 3, 4, 5, and 6—are equally likely. This is the key! There are other events whose probabilities can be calculated using this method.

Other probabilities calculated using this method are based on the key idea that outcomes are equally likely. Anytime you have outcomes that are equally likely, the theoretical probability method can be used, such as:

• A coin flip
• Drawing a card from a deck (the deck must be adequately shuffled)
• Selecting marbles from a jar (all marbles must be equal size so you have an equal probability of picking them out); they should also be well mixed.

formula to know

Theoretical Probability

term to know

Theoretical Probability

The method of assigning probability to events based on the assumption that all events are equally likely. The probability of an event is the equally likely ways an event can occur divided by the number of possible outcomes.

2. Unlikely Equal Outcomes

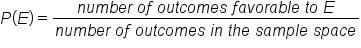
The theoretical probability model does not work if the outcomes aren't equally likely.

EXAMPLE

You could use this reasoning to say, for example, you could get home safely from work in your car, or you could get in a horrible car crash. Either is a possible outcome. If you assign those equal likelihoods, then the probability of you getting into a car crash is one half because there are only two outcomes. You either make it home safe, or you get in a crash.

However, we know from experience that the outcome of not having an accident is so much more likely than the outcome of having an accident. Therefore, equal probabilities are not assigned in this case because experience shows that those two outcomes are not equally likely.

did you know

The theoretical probability model is also called an "a priori method," which means it is known prior to, or beforehand.