The Venn Test of Validity

1. Two-Category Tests of Validity

Arguments with categorical sentences cannot be tested for validity in propositional logic. However, they can be tested using Venn diagrams and categorical logic.

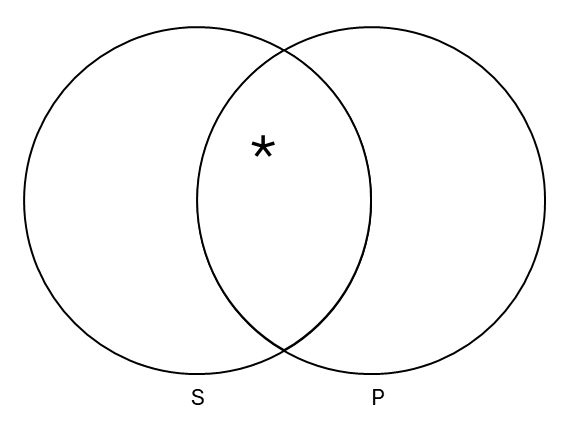
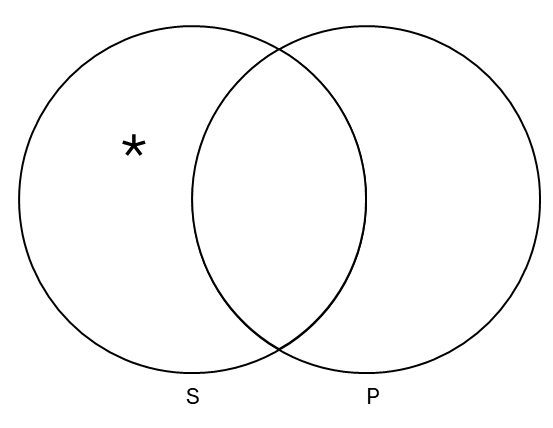
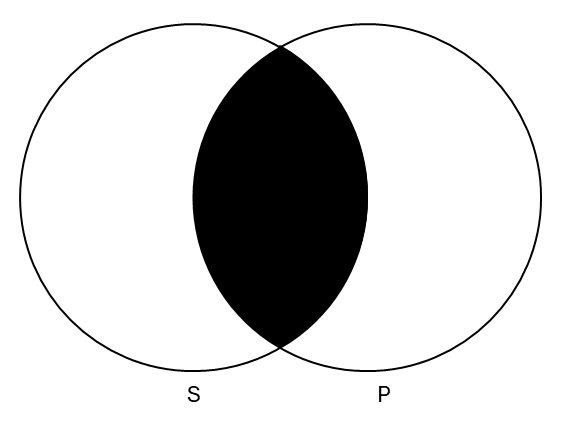
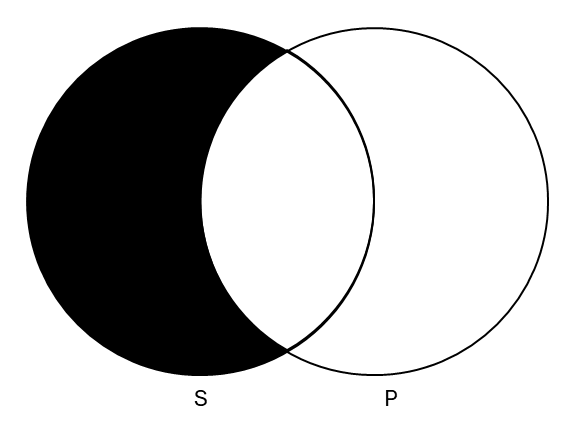
First, let’s review the four categorical sentence forms in Venn diagram form.

Some S are P	Some S are not P
No S are P	All S are P

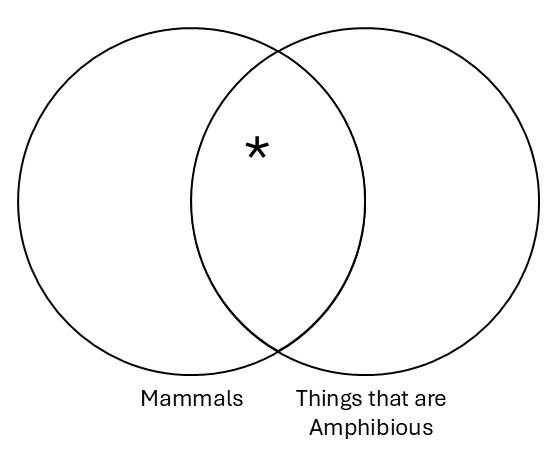
Now, let’s check the validity of a simple argument with one premise and one conclusion:

1. Some mammals are amphibious.
2. Therefore, some amphibious things are mammals.

If we construct a Venn diagram for the premise and another Venn diagram for the conclusion, we will see that the Venn diagrams are identical to each other. Remember that the asterisk means there is at least one thing in the group or groups indicated by that part of the diagram. You might remember that we noted the equivalence of these categorical forms in the previous section.

Some Mammals are Amphibious	Some Amphibious Things are Mammals

This argument passes the Venn test of validity because the conclusion Venn contains no additional information that is not already contained in the premise Venn. Thus, this argument is valid.

hint

In categorical logic, validity is proven by showing that the Venn diagram for the conclusion contains no more information than the Venn diagram for the premise(s).

watch

View a demonstration of this example.

Let’s now turn to an example of an invalid argument.

1. All cars are vehicles.
2. Therefore, all vehicles are cars.

Here are the Venns for the premise and the conclusion, respectively:

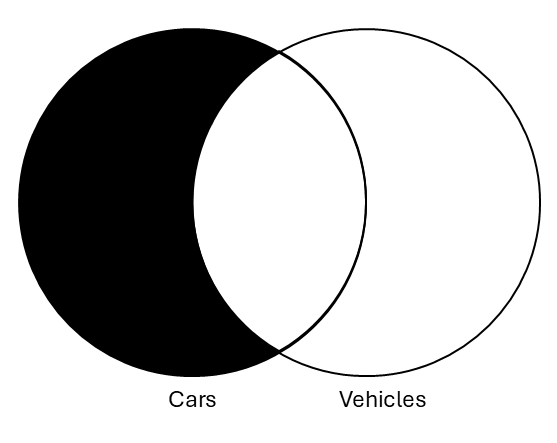
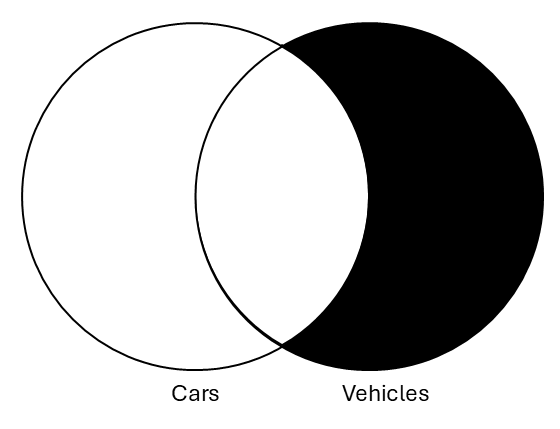
All cars are vehicles	All vehicles are cars
	]

In this case, the diagrams contain different information. More importantly, we can see that the conclusion (on the right) contains distinctly novel information from the premise diagram. The conclusion asserts that there cannot be anything in the “vehicle” category that isn’t also in the “car” category. However, this information isn’t in the premise, which says that there isn’t anything in the “car” category that isn’t also in the “vehicle” category. Thus, this argument fails the Venn test of validity since there is information in the conclusion that is not in the premise. This argument is invalid.

reflect

Have you heard (or even told) the riddle, "How do you know if someone is a vegan (or atheist, or skier, or the member of some other group)?" The punchline is, "They'll tell you!" This punchline is based on the same fallacy of categorical logic shown above. Because everybody in category S (people who tell you they are in category P) is in category P, every person in category P are presumed to be in category S. In fact, there are likely people you don't know are in category P because they haven't told you.

The Venn test of validity is a formal method like proofs and truth tables in sentential logic because we can apply it based on the categorical sentence form alone, without knowing what the categorical variables represent. We can simply use “S” and “P” to represent any subject and predicate category, respectively.

For example:

1. Some S are not P.
2. Therefore, no P are S.

Some S are not P	Therefore, no P are S

The conclusion (on the right) contains information that is not contained in the premise (on the left). The conclusion explicitly rules out that there is anything that is both in S and in P. In contrast, the premise says nothing about the possibility of things being both S and P. Thus, we can say that this argument fails the Venn test of validity and is invalid because the conclusion introduces the removal of a possibility. We know this even though we have no idea what the categories S and P are. This is the mark of a formal method of evaluation.

watch

View a demonstration of this example.

try it

Apply the Venn test of validity in order to determine whether the following categorical inferences are valid or invalid.

1. All S are P.
2. Therefore, all P are S.

1. Some S are P.
2. Therefore, some P are S.

Check Your Answer

The first is invalid.

The second is valid.

---

2. Testing Validity of Three-Category Venn Diagrams

So far, we have been looking at Venn diagrams with two categories. We now turn to Venn diagrams with three. The interpretation of these diagrams is the same as before, with each circle representing a category of things, and the intersections of all three circles representing the things that belong to all three categories.

2a. Three-Category Venn Diagrams

As you can see from the diagram below, with three circles, we have eight different regions. The eighth region is the one outside the circles. This is the set of presumed things that belong to none of the categories identified. Though in abstraction this concept might be difficult, think about it in concrete terms. If our three categories are “things that fly”, “reptiles,” and “mammals,” a guitar is an object that exists but isn’t in one of these three categories.

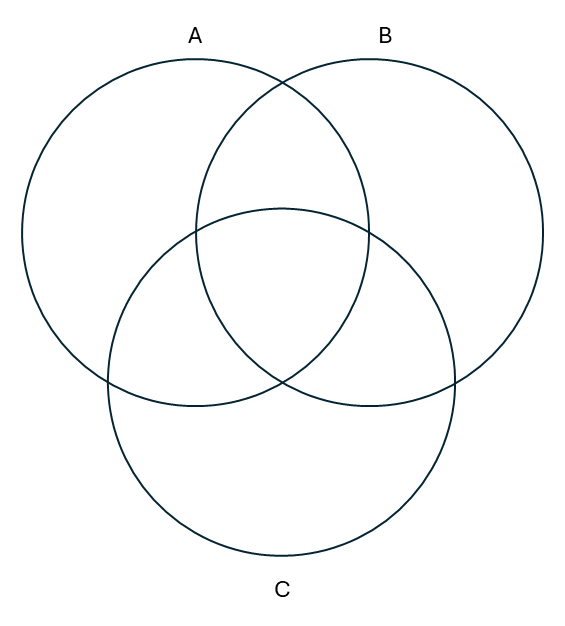
Here is an illustration of a three-circle diagram. In this example, we are not working from premises and a conclusion, simply showing the relationships between real-world categories.

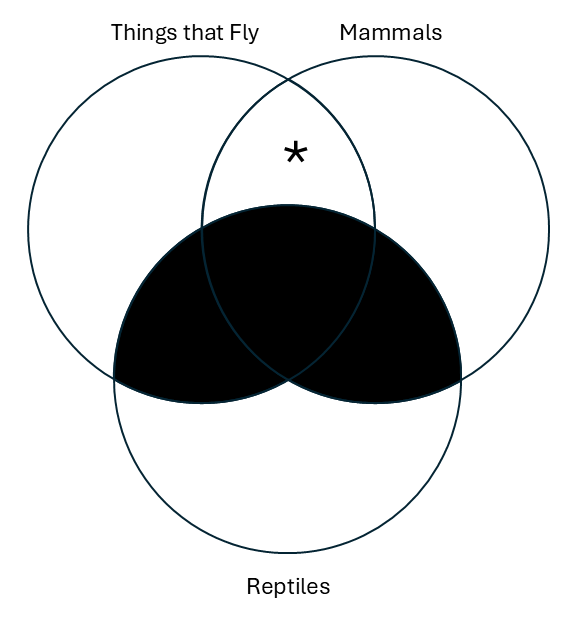
You can see from the intersection of categories A and B that there is at least one thing that can fly and is a mammal (a bat). However, the intersection of categories B and C show there is no thing that can fly and is a reptile (at least not currently alive). Moreover, there is no thing that is a reptile and a mammal. (Apologies to any lizard people taking this class!)

Note that if any intersection of two categories is shaded, the center must also be shaded. Because if something isn’t B and C, then it’s definitely not B, C, and A. If nothing is a reptile and a mammal, it can’t also be a flying reptile and mammal.

2b. Validity Tests of Three-Category Venn Diagrams

Recall that syllogism is an argument where the conclusion follows from two premises; a categorical syllogism is syllogism involving at most three categories. As we have seen, there are four different forms of categorical sentences:

• All S are P (universal positive)
• No S are P (universal negative)
• Some S are P (particular positive)
• Some S are not P (particular negative)

Here is a classic example:

1. All humans are mortal.
2. All mortal things die.
3. Therefore, all humans die.

Each one of the statements in this syllogism is a universal positive of the form “All S are P.” Let’s first translate each to a categorical paraphrase:

1. All humans are things that are mortal.
2. All things that are mortal are things that die.
3. All humans are things that die.

In determining the validity of a categorical syllogism, we must construct a three-category Venn diagram for the premises and a two-category Venn diagram for the conclusion. Here is what the three-category Venn looks like for the premises:

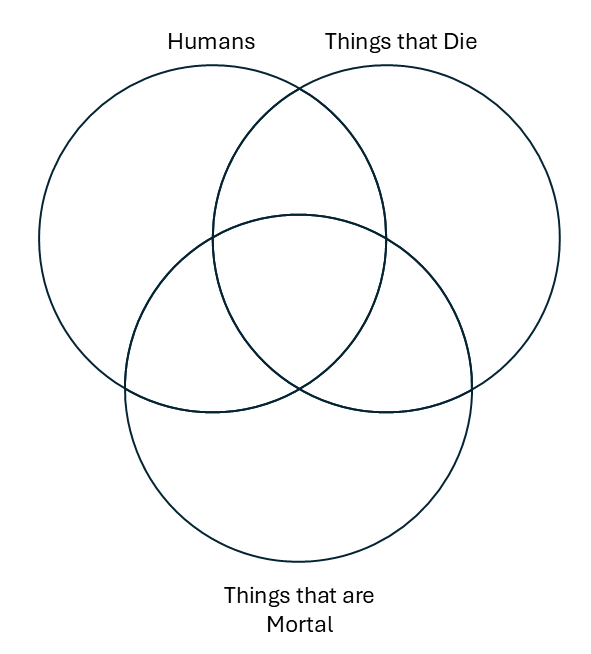
The next thing we need to do is represent the information from the two premises in our three-category Venn. We'll start with the first premise, which says, “All humans are things that are mortal.”

try it

How do you shade or mark the Venn diagram to represent this statement?

You need to shade any part of the circle for “humans” that is not overlapping with “things that are mortal.” Our Venn diagram looks like this:

The next thing we have to do is fill in the information for the second premise, “All things that are mortal are things that die.”

try it

How do you shade or mark the Venn diagram to represent this statement?

We will now block out that part of “Things that are mortal”) that does not intersect with the “Things that die” category. Our Venn now looks like this:

The next thing we have to do is construct a two-category Venn for the conclusion. The conclusion states there is nothing in the “humans” category that isn’t also in the “things that die” category. It also allows that there are things that die, but that aren’t humans. Last, we compare this to the three-category Venn (or premises Venn) to see if they are the same.

Premises Venn	Conclusion Venn

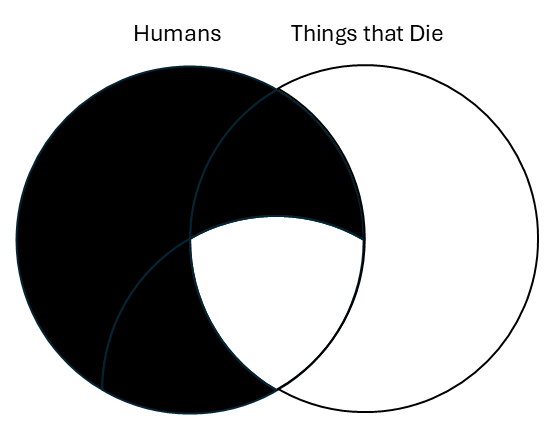
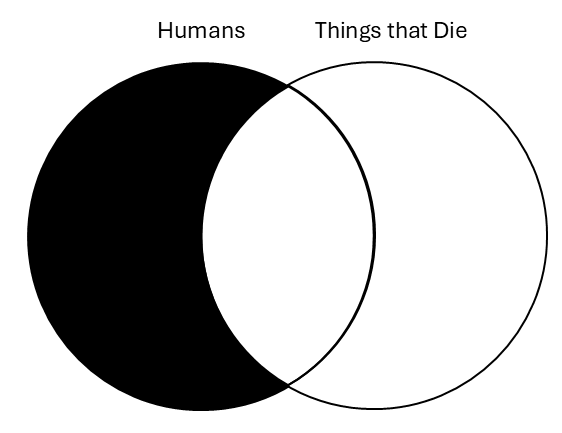
The relevant points of comparison are the “humans” and “things that die” categories. Do the two circles have the same shading? They do not. In the premises Venn, part of the intersection between the two is shaded; but in the conclusion Venn, the intersection is not shaded. Since they do not look exactly alike, we must ask whether the conclusion Venn contains more information than the premise Venn. In the premise Venn, every part of the “humans” category that is outside the “things that die” category is shaded. The conclusion Venn only rules out humans that don’t die. The premise Venn rules out the same (in fact, more) possibilities as the conclusion Venn; the conclusion thus doesn’t contain more information than the premises. Thus, this argument passes the Venn test of validity.

Note that it doesn’t matter that the premise Venn contains more information than the conclusion Venn. That is to be expected, since the premise Venn represents a whole other category that the conclusion Venn isn’t. This is allowable. What isn’t allowable (and thus would make an argument fail the Venn test of validity) is if the conclusion Venn contained information that wasn’t already contained in the premise Venn.

step by step

Let’s try testing the argument we used to open this challenge. Follow each step on your own before you check how we completed it.

1. Some cats are pets.
2. All pets are well cared for.
3. Therefore, some cats are well cared for.

For the first step, name the three categories we will use in this test of validity. Remember that they must be countable things.

Check Your Answer

The three categories are:

1. Cats
2. Pets
3. Things that are well cared for

The next step is to create your Venn with overlapping circles.



The next step is to shade and mark the diagram to represent the premises.

1. Some cats are pets.
2. All pets are [things that are] well cared for.

Do this and then check your answer.

Check Your Answer

We first place a mark on the intersection of “cats” and “pets” to show there is at least one thing that is both a cat and a pet. But where should we put it? There are two areas, one showing just an overlap of pets and cats, the other showing the overlap of all three categories. In fact, there is a rule for shading that helps us with just this problem: we should do the universal sentences first. So, let’s do the second premise first, and come back to the first premise after.

We should shade all of the circle for “pets” that is not part of the circle for “things that are well cared for.” We place our asterisk in the intersection of all three categories. This means there is at least one cat that is a pet, and as a pet, it is well cared for. Since all pets are things that are well cared for, any intersection between “cats” and “pets” that does not also intersect with “things that are well cared for” is ruled out. So, when we return for premise 1, the only place to put our asterisk that is in the intersection of “cats” and “pets” must also be in the intersection with “things that are well cared for” because the universal in premise 2 eliminates possibilities outside that category.

Now that we have our premises Venn, we should do the conclusion. What will that look like? The statement we need to represent is, “Some cats are [things that are] well cared for.” Create your own before you check your answer.

Check Your Answer

As we did above, we use a mark to show there is at least one thing in the S category with the P category—in this case, at least one cat that is well cared for. While our 3-circle Venn has some areas that are shaded that are not in our 2-circle Venn, they are not at the intersection of Pets and Things that are Well-Cared For, so this time we can see right away that the conclusion is valid.


The conclusion does not have any information that is not in the premises Venn diagram, so the argument is valid.

2c. Ambiguity in Venn Diagrams

Let’s look at one more example of a three-category argument.

1. Some mammals are bears.
2. Some two-legged creatures are mammals.
3. Therefore, some two-legged creatures are bears.

We will encounter a similar dilemma to the one we had above. When we go to place our asterisk to show that at least one bear is a mammal, we don’t know (from the premises) whether to put it in the area where all three circles overlap or just two for bears and mammals.

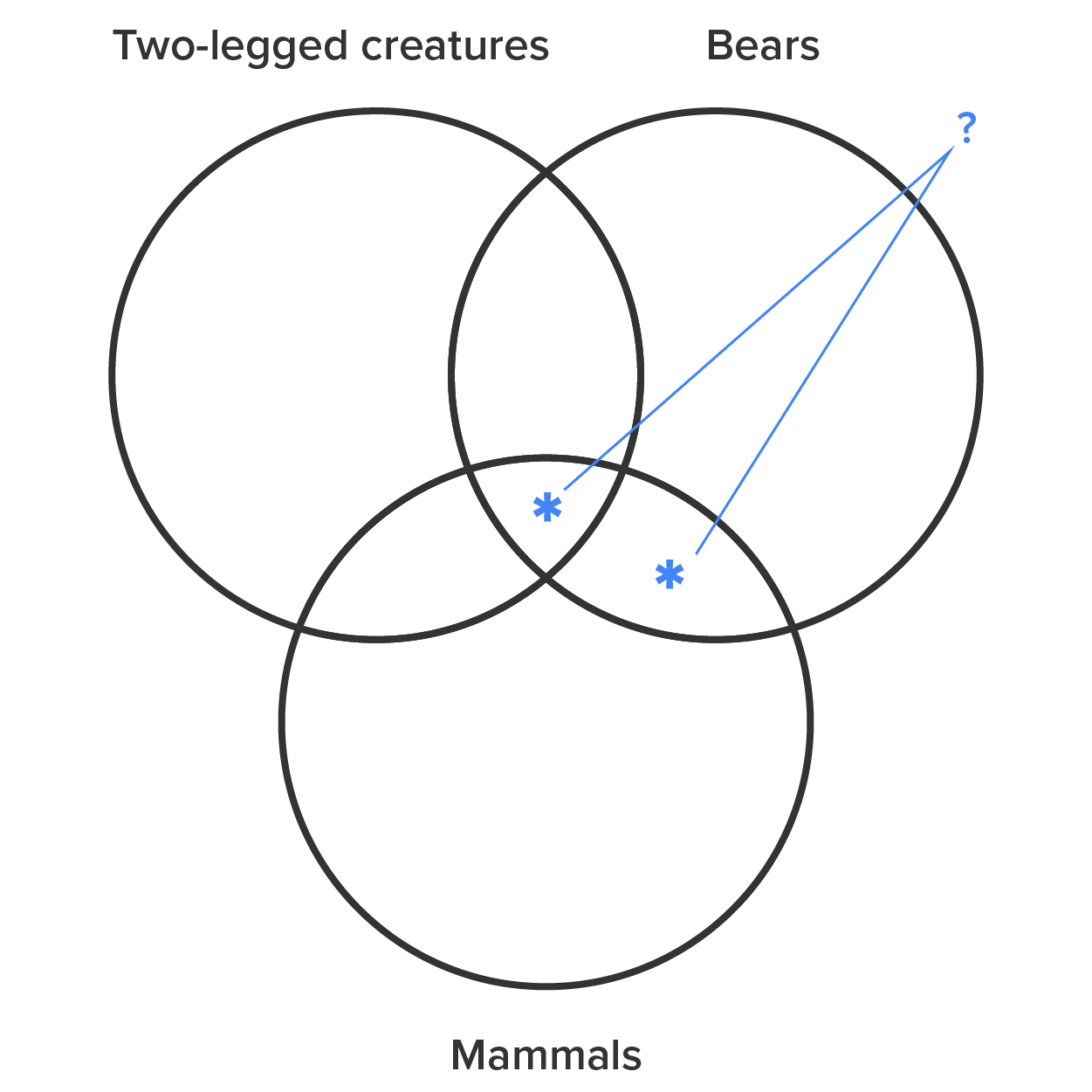
In the problem above, we were able to quickly clear this up by first shading for the universal sentence, but here we do not have a universal. The next premise here presents the same dilemma. We have to represent that there is at least one thing that is both a bear and a mammal, but is it also two-legged? Unfortunately, we have also reached the end of our premises, so there will be no more information to guide us.

Thus, in order to accurately represent the information contained in this premise, we must adopt a new convention. That convention says that when we encounter a situation where we must represent a particular between two categories on a three-category Venn and don’t know whether the particular also belongs in the third category, then we must put the asterisk on the line in between the two areas in which it might belong. This is what the Venn diagram will look like when we have noted there is at least one bear that is a mammal that may or may not be two-legged.

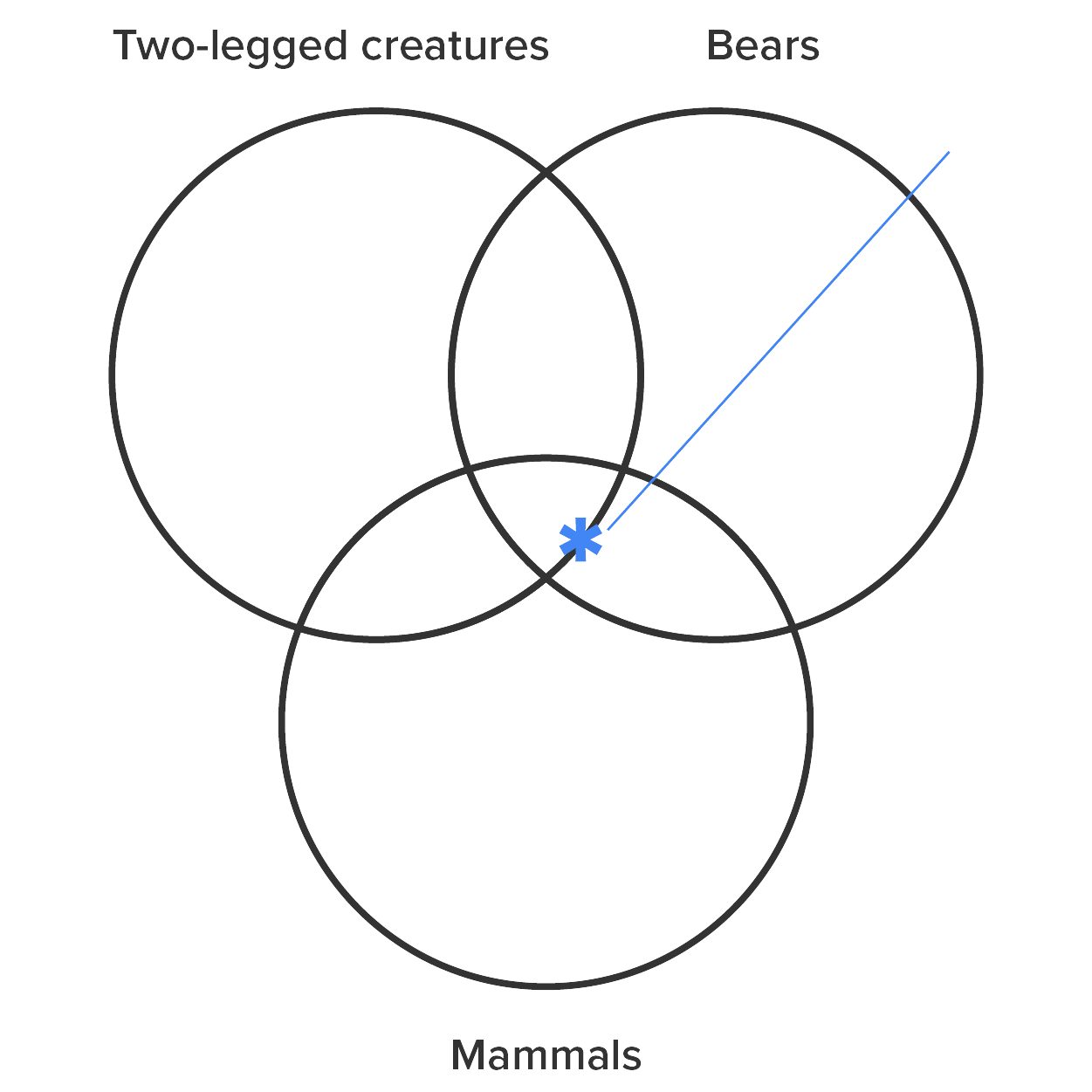
We must do this same thing for the second premise since we encounter the same problem. We know there is at least one two-legged mammal, but do not know from the premises if it is or is not a bear. So once again we place the asterisk on the border between the two possibilities.

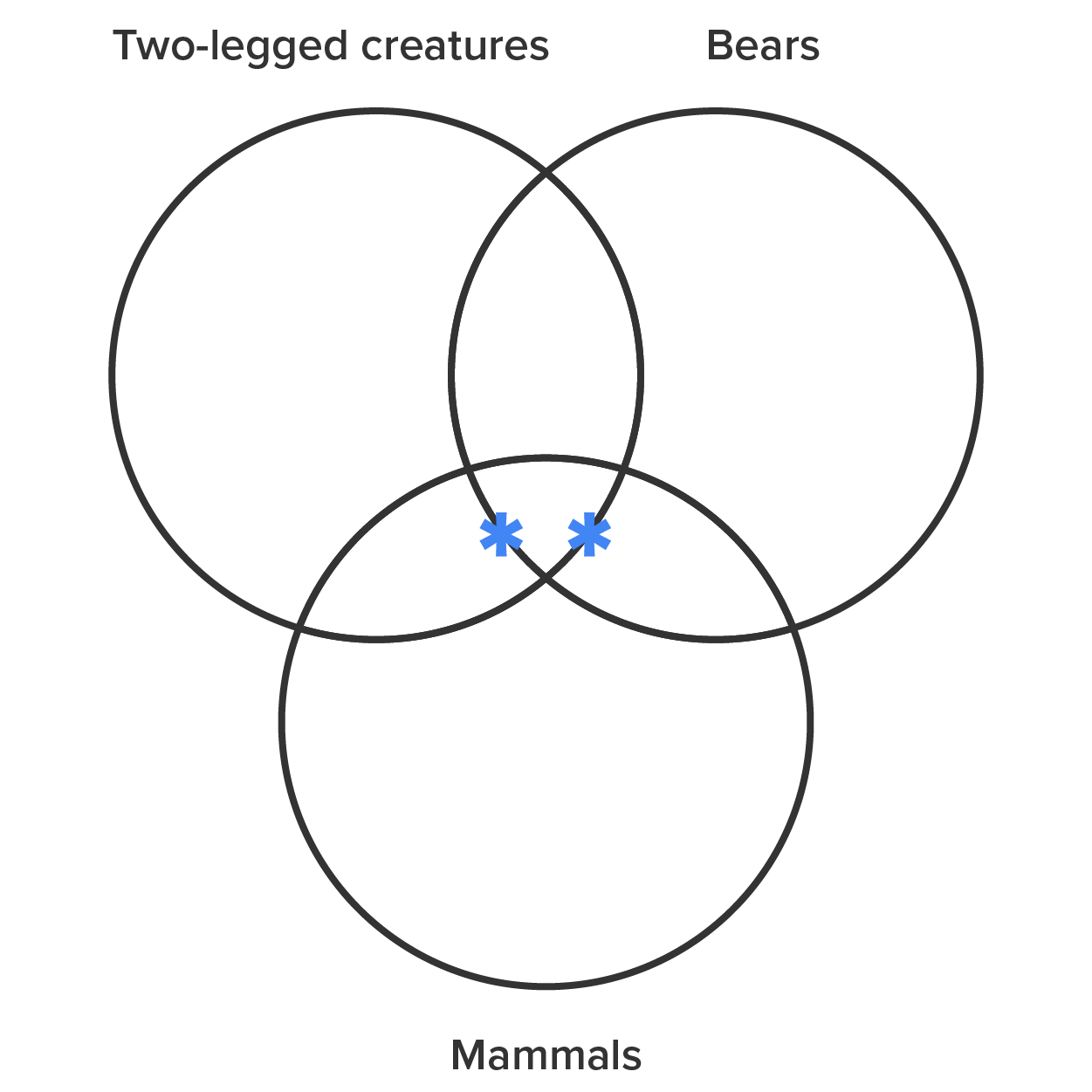
We can draw no more conclusions from these premises, so let’s diagram the conclusion, which states that some two-legged creatures are bears.

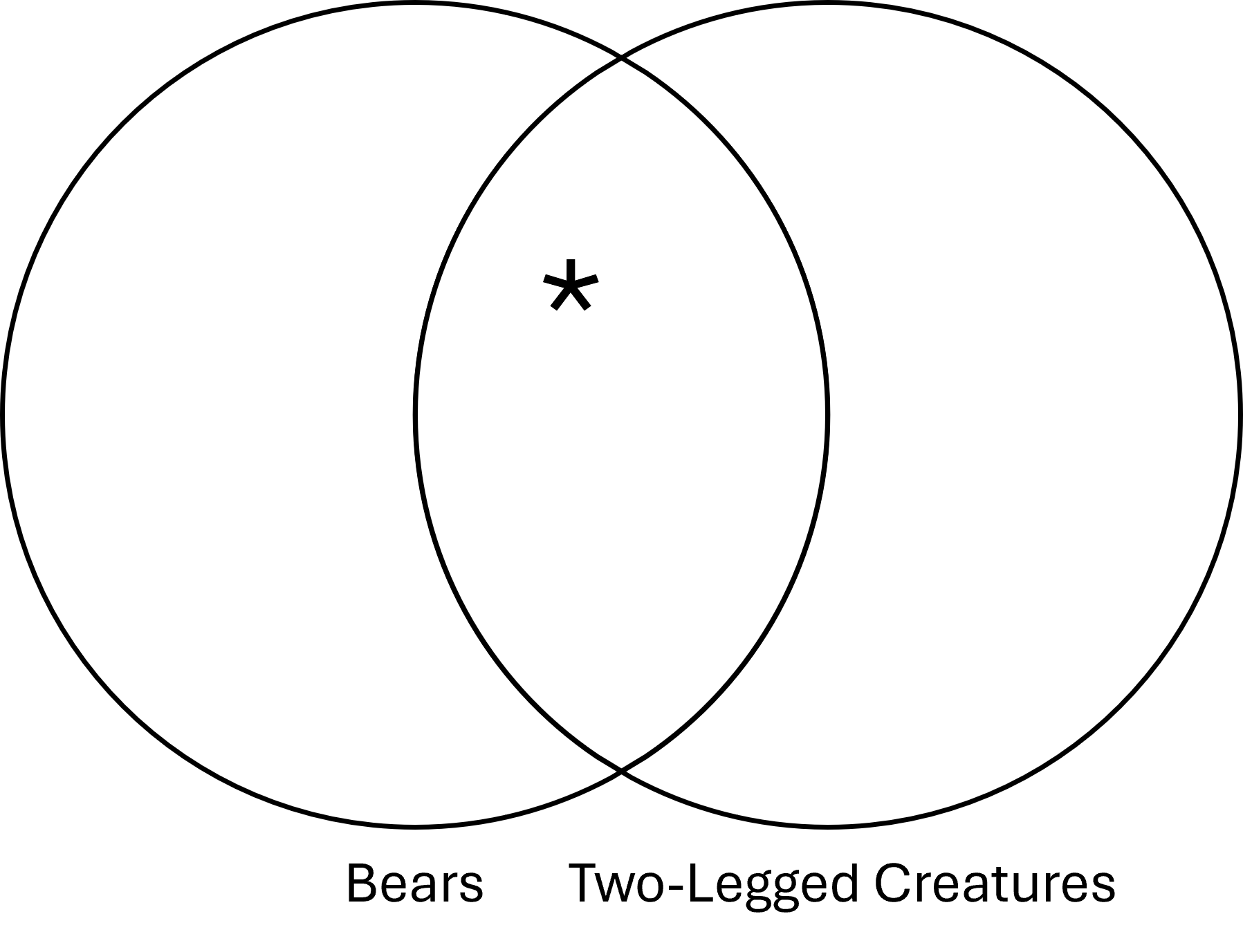
We can see that this argument fails the Venn test of validity because the conclusion contains information not in the premises. The conclusion asserts that there is at least one thing that is both a two-legged creature and a bear, while the premises Venn contains no such information.

try it

Use a three-category Venn diagram to check the validity of this argument:

1. All mice are rodents.
2. All mice are omnivores.
3. All rodents are omnivores.

Check Your Answer

Your three-category Venn will look like this:



Your two-category Venn will look like this:



You can see it has information that is not in the premises: the conclusion Venn rules out the possibility of non-omnivore rodents, but the premise Venn does not. While it is in fact a true statement, it does not logically follow from the premises, and the argument is invalid.