Table of Contents |
Consider the function 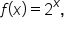 whose table of values and graph are shown below.
whose table of values and graph are shown below.

|
|
|---|---|
| 0 |
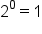
|
| 1 |
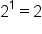
|
| 2 |
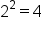
|
| 3 |
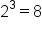
|
| 4 |
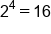
|
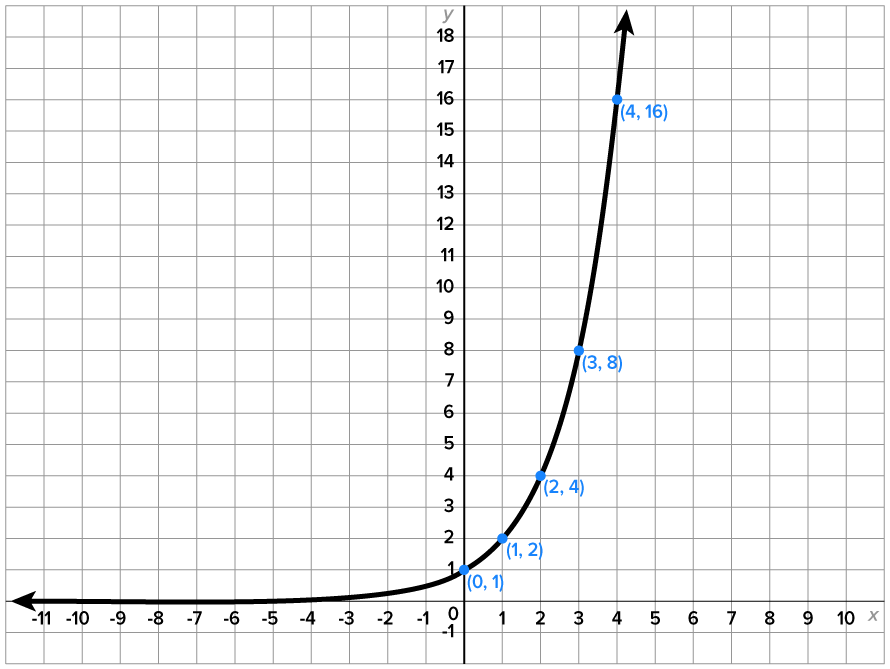
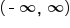
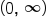
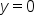
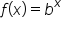 passes the horizontal line test,
passes the horizontal line test,  is one-to-one and therefore has an inverse function. We say that
is one-to-one and therefore has an inverse function. We say that  has the one-to-one property.
has the one-to-one property.
The one-to-one property for exponential functions tells us that if two exponential expressions with the same base are equal to each other, then the exponents must also be equal. The property also tells us that if two quantities are equal, then using them both as exponents on the same base will produce the same result.
This property will be used more frequently when solving equations.
Recall that to find an inverse of a one-to-one function, interchange its inputs and outputs. The table of values of the inverse function are shown below.

|
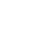
|
|---|---|
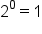
|
0 |
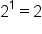
|
1 |
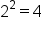
|
2 |
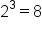
|
3 |
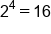
|
4 |
Notice some patterns in the inverse function. For example:
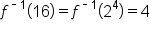
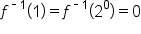
Since the inverse of an exponential function is important, we need to give it a name.
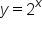
|
Replace  with y. with y.
|
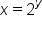
|
Interchange x and y. |
Another word for exponent is logarithm.
We rewrite the equation 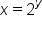 as
as 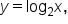 which is “the logarithm with base 2 of x.”
which is “the logarithm with base 2 of x.”
Therefore, the inverse of 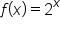 is
is 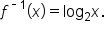
 and
and  the inverse of
the inverse of 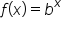 is
is 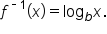
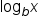 or
or 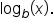 The quantity x is often called the argument of the function.
The quantity x is often called the argument of the function.
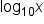 ” is written as “
” is written as “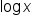 .” This means
.” This means 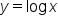 is equivalent to
is equivalent to 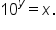 Note: a logarithm with base 10 is also called a common logarithm.
Note: a logarithm with base 10 is also called a common logarithm.
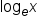 ” is written as “
” is written as “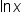 ,” which is called the “natural logarithm of x.” This means
,” which is called the “natural logarithm of x.” This means  is equivalent to
is equivalent to 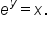
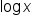 ” in place of “
” in place of “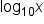 ” is because our number system is base 10 (which comes from us having 10 fingers). It is also easier to measure in powers of 10. That said, there is nothing incorrect about writing “
” is because our number system is base 10 (which comes from us having 10 fingers). It is also easier to measure in powers of 10. That said, there is nothing incorrect about writing “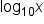 ,” it is just that “
,” it is just that “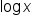 ” is a shorter way of writing it.
” is a shorter way of writing it.
EXAMPLE
Consider the functions and
and 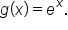
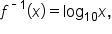 which is then written
which is then written 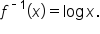
 which is written
which is written 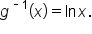
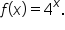
Using the definition of a logarithm is useful for writing a logarithmic expression in exponential form, and vice versa. First, we will look at writing a logarithm in exponential form.
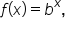 where
where 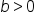 and
and 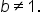 Then, for quantities R and S,
Then, for quantities R and S, 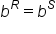 if and only if
if and only if 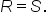
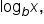 it is the real number y for which
it is the real number y for which 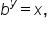 where
where 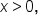
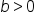 , and
, and 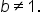
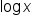 in place of
in place of 
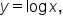 then
then 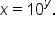
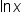 in place of
in place of 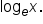
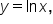 then
then 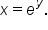
Given a logarithmic equation, we can use the fact that 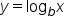 means
means 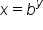 to write the corresponding exponential equation.
to write the corresponding exponential equation.
Where appropriate, remember that 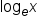 is written as
is written as 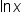 , and
, and 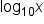 is written as
is written as 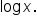
EXAMPLE
Convert each logarithmic equation to its corresponding exponential form.| Logarithmic Equation | Exponential Form |
|---|---|
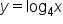
|
This equation in exponential form is 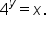
|
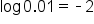
|
Remember that “log 0.01” with no base written is assumed to be base 10. If it helps, write 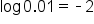 as as 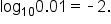
Then, the exponential form is 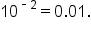
|
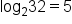
|
This equation in exponential form is 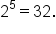
|
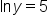
|
Remember that “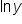 ” means that the base is e. If it helps you, write ” means that the base is e. If it helps you, write 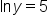 as as 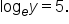
Then, the exponential form is 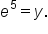
|
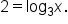
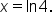
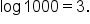
In some circumstances, notice that writing the equation in exponential form helps to see what the value of x is that makes the statement true. For example, the logarithmic equation 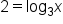 has exponential form
has exponential form 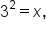 which means
which means 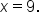 In this case, writing the exponential form helped to solve the equation for x.
In this case, writing the exponential form helped to solve the equation for x.
Now, we’ll write exponential equations in their corresponding logarithmic form.
From earlier, we know that given 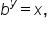 then
then 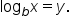 Remember the special cases for base 10 and base e.
Remember the special cases for base 10 and base e.
EXAMPLE
Convert each exponential equation to its corresponding logarithmic form.| Exponential Form | Logarithmic Equation |
|---|---|
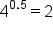
|
Its corresponding logarithmic form is 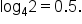
|
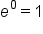
|
The corresponding logarithmic form is 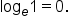 To simplify this, remember that “ To simplify this, remember that “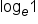 ” can be replaced with “ ” can be replaced with “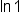 .” .”
The final answer is 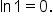
|
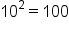
|
The corresponding logarithmic form is 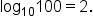 To simplify this, remember that “ To simplify this, remember that “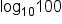 ” can be replaced with “ ” can be replaced with “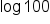 .” .”
The final answer is 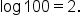
|
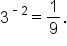
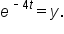
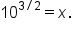
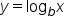 means
means 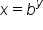 to write the corresponding exponential form. Conversely, when writing exponential equations in logarithmic form, you learned that given
to write the corresponding exponential form. Conversely, when writing exponential equations in logarithmic form, you learned that given 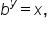 then
then 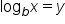 , noting the special cases for base 10 and base e.
, noting the special cases for base 10 and base e.
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.