Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

The Linear Approximation Error | f(x) – L(x) |

Author: Sophia
PDF Version

what's covered
In this lesson, you will investigate the error in using a linear approximation to approximate the value of a function. Specifically, this lesson will cover:

Table of Contents

1. Calculating the Error in Using L(x) to Approximate f  (x)

It is no surprise that using the linear approximation will produce some error.

The linear approximation error is the difference between the actual function value and the value obtained through the linear approximation.

formula to know
Linear Approximation Error
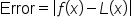
Error equals open vertical bar f open parentheses x close parentheses minus L open parentheses x close parentheses close vertical bar

hint
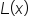The error formula has an absolute value since we are only concerned with the size of the error, not necessarily which of L open parentheses x close parentheses or f open parentheses x close parentheses is larger. With absolute value, the difference is nonnegative regardless.

EXAMPLE

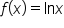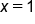Consider the function f open parentheses x close parentheses equals ln x near x equals 1. We’ll use the linear approximation to estimate 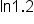ln 1.2, then find the linear approximation error.

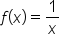
To find the linear approximation, first find the derivative: f open parentheses x close parentheses equals 1 over x

Now, form the linear approximation:

L open parentheses x close parentheses equals f open parentheses a close parentheses plus f apostrophe open parentheses a close parentheses open parentheses x minus a close parentheses Use the equation for the tangent line.
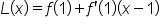
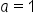
L open parentheses x close parentheses equals f open parentheses 1 close parentheses plus f apostrophe open parentheses 1 close parentheses open parentheses x minus 1 close parentheses a equals 1
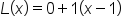
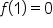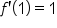
L open parentheses x close parentheses equals 0 plus 1 open parentheses x minus 1 close parentheses f open parentheses 1 close parentheses equals 0 and f apostrophe open parentheses 1 close parentheses equals 1
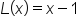
L open parentheses x close parentheses equals x minus 1 Simplify.

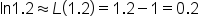The linear approximation tells us that ln 1.2 almost equal to L open parentheses 1.2 close parentheses equals 1.2 minus 1 equals 0.2.

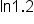The actual value of ln 1.2 is 0.1823 (to 4 decimal places).

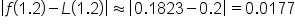Then, the linear approximation error is open vertical bar f open parentheses 1.2 close parentheses minus L open parentheses 1.2 close parentheses close vertical bar almost equal to open vertical bar 0.1823 minus 0.2 close vertical bar equals 0.0177.

try it
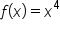Consider the function f open parentheses x close parentheses equals x to the power of 4. Use the linear approximation at 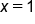x equals 1 to estimate 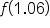f open parentheses 1.06 close parentheses. Then, find the linear approximation error to 4 decimal places.
What is the linear approximation?
First, find the linearization, L open parentheses x close parentheses equals f open parentheses 1 close parentheses plus f apostrophe open parentheses 1 close parentheses open parentheses x minus 1 close parentheses.

Note that f open parentheses 1 close parentheses equals 1 to the power of 4 equals 1.

f apostrophe open parentheses x close parentheses equals 4 x cubed comma which means f apostrophe open parentheses 1 close parentheses equals 4 open parentheses 1 close parentheses cubed equals 4.

Thus, the linearization is L open parentheses x close parentheses equals 1 plus 4 open parentheses x minus 1 close parentheses.

Then, the approximation when x equals 1.06 is L open parentheses 1.06 close parentheses equals 1 plus 4 open parentheses 1.06 minus 1 close parentheses equals 1.24.
What is the linear approximation error?
To find the actual error, first compute f open parentheses 1.06 close parentheses equals 1.06 to the power of 4 equals 1.26247696.

Then, the error is open vertical bar f open parentheses x close parentheses minus L open parentheses x close parentheses close vertical bar equals open vertical bar 1.26247696 minus 1.24 close vertical bar almost equal to 0.0225.

2. Analyzing Error as x Gets Further Away From a

In 3.4.1, we used 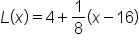L open parentheses x close parentheses equals 4 plus 1 over 8 open parentheses x minus 16 close parentheses to approximate 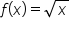f open parentheses x close parentheses equals square root of x for values of x near 16.

Here is a table of values (rounded to four decimal places) to illustrate what happens to the error as x moves away from 16:

x bold italic L open parentheses bold x close parentheses bold equals bold 4 bold plus bold 1 over bold 8 open parentheses bold x bold minus bold 16 close parentheses bold italic f open parentheses bold x close parentheses bold equals square root of bold x Errorbold equals open vertical bar bold f open parentheses bold x close parentheses bold minus bold L open parentheses bold x close parentheses close vertical bar
16.25 4.0313 4.0311 0.0002
16.5 4.0625 4.0620 0.0005
16.75 4.0938 4.0927 0.0011
17 4.1250 4.1231 0.0019
17.25 4.1563 4.1533 0.0030
17.5 4.1875 4.1833 0.0042
17.75 4.2188 4.2131 0.0057
18 4.2500 4.2426 0.0074

As you can see, even though the errors are relatively small, they are increasing as x increases from 16. We would see a similar pattern if x were to decrease from 16 (15.75, 15.5, etc.).

summary
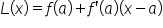In this lesson, you learned how to calculate the linear approximation error, or the error in using L(x) to approximate f (x). The linear approximation error is found by calculating the positive difference between the linear approximation and the actual value. You also learned that when considering the linear approximation L open parentheses x close parentheses equals f open parentheses a close parentheses plus f apostrophe open parentheses a close parentheses open parentheses x minus a close parentheses, the error gets larger as x gets further from a.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 2 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Formulas to Know
Linear Approximation Error

Error equals open vertical bar f open parentheses x close parentheses minus L open parentheses x close parentheses close vertical bar

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.