Table of Contents |
Consider an oblique triangle. Another set of relationships that can be used to find unknown sides and angles of an oblique triangle is known as the law of cosines.
Remember:
 is opposite angle
is opposite angle 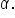
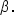
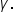
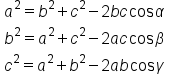
For simplicity, the law of cosines is used when either the side on the left side of the equation is not known or the angle is unknown.
EXAMPLE
A triangle has sides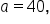
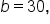 and angle
and angle 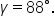 Find the remaining side and angles.
Find the remaining side and angles.
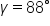 is included between the given sides, which means the law of cosines can be used to find the unknown side.
is included between the given sides, which means the law of cosines can be used to find the unknown side.
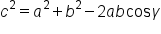
|
Use this version since 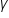 was given. was given.
|
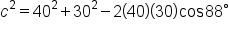
|
Replace known sides and angles by their values. |
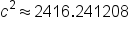
|
Approximate the right side. |
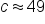
|
Apply the square root principle to find the value of c. Note that only the positive solution is considered. |
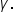 However, remember that we need to check the second solution that comes from the law of sines.
However, remember that we need to check the second solution that comes from the law of sines.
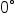 and
and 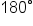 inclusive, meaning that there is only one unique answer for the angle.
inclusive, meaning that there is only one unique answer for the angle.
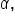 we will use the law of cosines.
we will use the law of cosines.
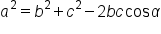
|
Use this version since it contains 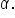
|
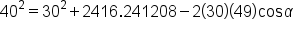
|
Substitute all known values. To preserve accuracy, note that 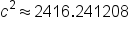 from above is used. from above is used.
|
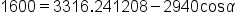
|
Simplify. |
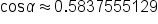
|
Subtract 3316.241208 from both sides, then divide both sides by -2940 to isolate 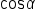 on one side. on one side.
|
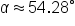
|
Apply the inverse cosine function and then round  to two decimal places. to two decimal places.
|
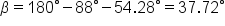
| Sides | Angles |
|---|---|
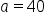
|
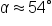
|
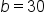
|
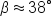
|
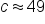
|
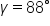
|
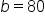 and
and 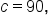 with included angle
with included angle 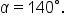 All sides are measured in inches.
All sides are measured in inches.
When three lengths are given, the law of cosines can be used to determine the angles opposite each side.
EXAMPLE
A triangle is to have sides with lengths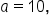
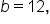 and
and 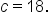 Find the angles of the triangle to the nearest degree.
Find the angles of the triangle to the nearest degree.
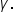
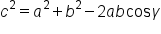
|
Use the formula that contains 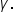
|
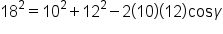
|
Substitute known quantities. |
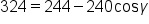
|
Simplify. |
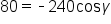 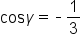
|
Isolate 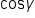 on one side. on one side.
|
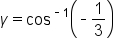
|
Apply the inverse cosine function. |
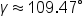
|
Approximate to two decimal places. |
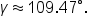
|
Use the formula that contains 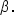
|
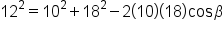
|
Substitute known quantities. |
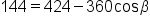
|
Simplify. |
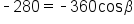 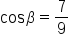
|
Isolate 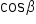 on one side. on one side.
|
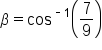
|
Apply the inverse cosine function. |
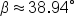
|
Approximate to two decimal places. |
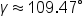 and
and 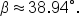
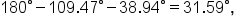 here is the set of all sides and angles in this triangle, rounded to the nearest degree:
here is the set of all sides and angles in this triangle, rounded to the nearest degree:
| Sides | Angles |
|---|---|
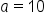
|
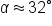
|
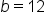
|
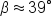
|

|

|
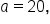
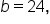 and
and 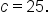
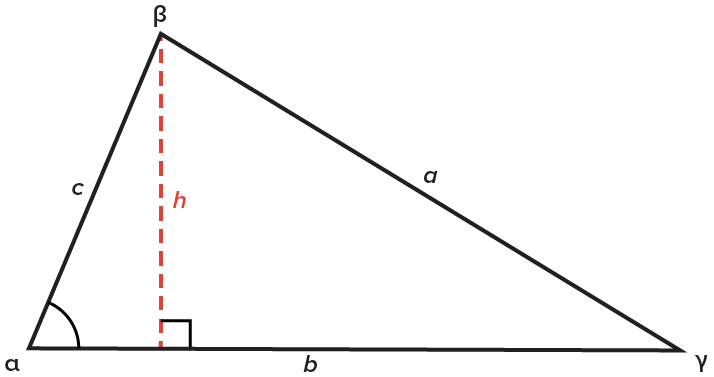
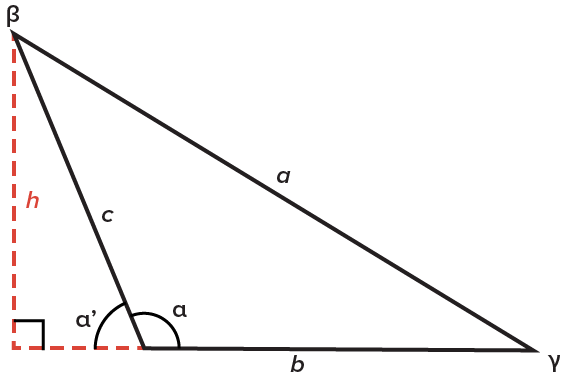
An acute triangle is a triangle in which all angles are less than  An obtuse triangle is a triangle in which one angle is more than
An obtuse triangle is a triangle in which one angle is more than 
Recall that the area of a triangle is 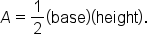
| Acute Triangle | Obtuse Triangle |
|---|---|
|
|
In order to find the area of an oblique triangle, we need an expression for the height.
In the acute triangle, we have 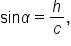 which means
which means 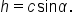
In the obtuse triangle, we have 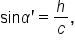 which means
which means 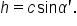
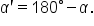
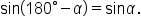
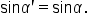
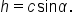
This means that the area of the triangle is 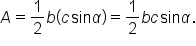
Note that in this formula, angle  is formed by sides b and c, meaning that
is formed by sides b and c, meaning that  is the included angle of sides b and c.
is the included angle of sides b and c.
Using the formula we derived above, there are two other versions of this form of the area of a triangle.
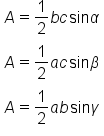
EXAMPLE
A triangle has two sides, one of length 50 cm and the other of length 90 cm, and an angle of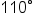 between the sides. Find the area of the triangle to the nearest whole number.
between the sides. Find the area of the triangle to the nearest whole number.
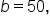
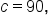 and
and 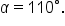
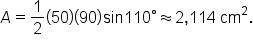


From earlier, the area of an oblique triangle is found by knowing two sides and the included angle. When three sides of a triangle are known, it is not necessary to find one of the angles in order to find the area of the triangle.
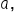 b, and c. Let
b, and c. Let 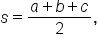 which is called the semiperimeter of the triangle.
which is called the semiperimeter of the triangle. 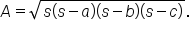
EXAMPLE
A triangle has sides with lengths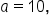
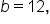 and
and 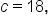 where all sides are measured in feet. Then, we can use Heron’s formula to find the area of the triangle to the nearest tenth, as follows.
where all sides are measured in feet. Then, we can use Heron’s formula to find the area of the triangle to the nearest tenth, as follows.
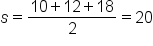
|
Find the semiperimeter using the given sides. |
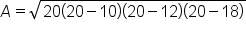
|
Substitute all known values into Heron’s formula. |
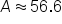
|
Approximate to the nearest tenth. |
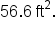
We can now expand our abilities to solve application problems to situations modeled by oblique triangles that lend themselves to using the law of cosines to find unknown information.
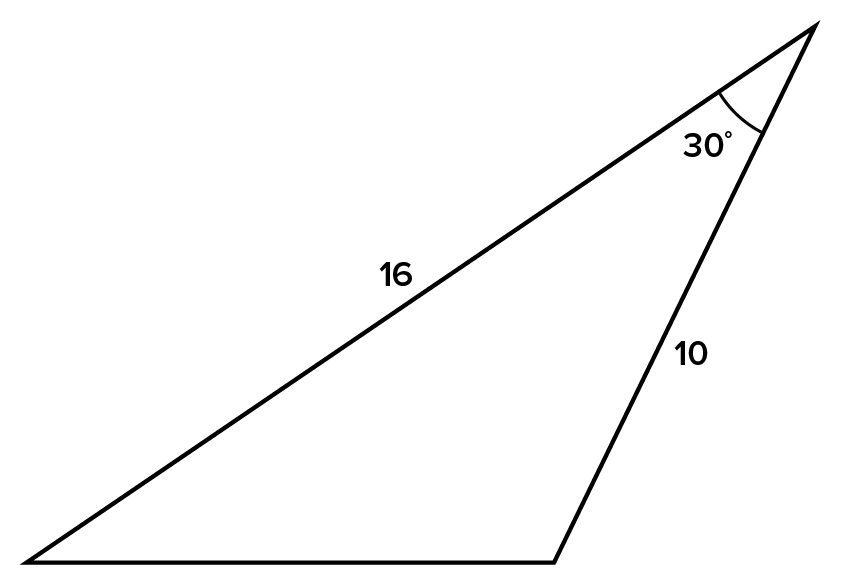
EXAMPLE
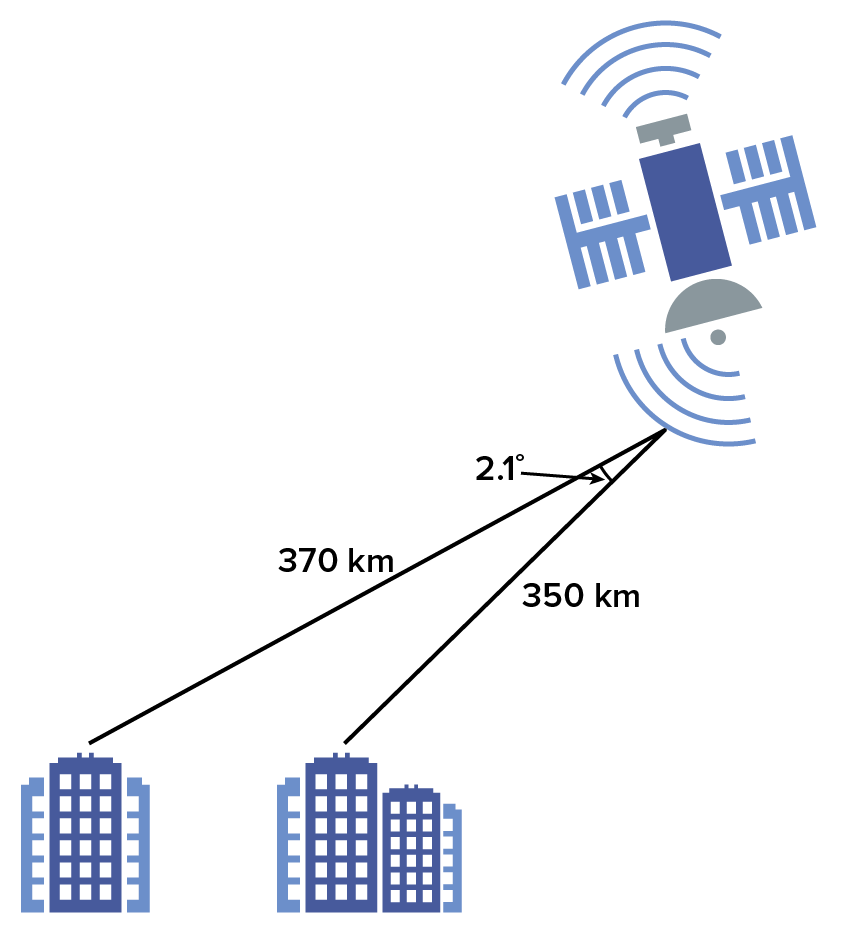
A surveyor has made the following measurements at two ends of the lake. What is the approximate distance across the lake to the nearest foot?
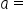 the unknown side. Then,
the unknown side. Then, 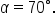 Since the other two sides are known, we then use the law of cosines to find the length of the lake.
Since the other two sides are known, we then use the law of cosines to find the length of the lake.
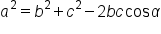
|
Use this version of the law of cosines since it contains 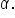
|
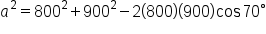
|
Let 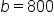 and and 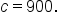 This is an arbitrary choice. The calculation does not change if This is an arbitrary choice. The calculation does not change if 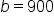 and and 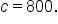
|
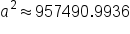
|
Simplify. |
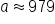
|
Apply the square root principle. Note that only the positive solution is considered. |
 then make sure the side opposite the angle is named
then make sure the side opposite the angle is named  Once that is established, it doesn’t matter which side is called b and which is called c.
Once that is established, it doesn’t matter which side is called b and which is called c.
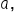 b, and c and angles
b, and c and angles 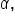
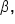 and
and 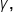 also remembering that side
also remembering that side  is opposite angle
is opposite angle 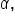 side b is opposite angle
side b is opposite angle 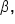 and side c is opposite angle
and side c is opposite angle 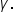 It’s also very helpful to organize your work with a table such as the one below to emphasize these relationships:
It’s also very helpful to organize your work with a table such as the one below to emphasize these relationships:
|
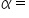
|
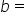
|
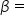
|
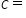
|
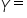
|
SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS