Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

The Intuitive Approach

Author: Sophia
PDF Version

what's covered
In this lesson, you will demonstrate the definition of a limit by finding the value of δ that corresponds to a given ε for a specific limit. Specifically, this lesson will cover:

Table of Contents

1. Finding the Value of δ That Corresponds to a Given Value of ε for a Linear Function

Recall a general limit statement: 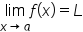limit as x rightwards arrow a of f open parentheses x close parentheses equals L

Based on methods we talked about in this course so far, the general idea is that the value of f open parentheses x close parentheses gets closer to L as x gets closer to a. A graph with an x-axis and a y-axis depicts a curve representing the function y equals f(x). The x-axis is labeled ‘a’, and the y-axis is labeled at three points: ‘L– ε’, ‘ε’, and ‘L+ ε’. The curve rises from the lower part of the graph, approaches the point (a, L), dips slightly, and then rises again. Three dashed horizontal lines at y equals L – ε, y equals L, and y equals L + ε intersect the curve at different points. A curved arrow pointing toward the y-axis between L+ ε and L is labeled ‘y is within ε of L’. A dashed vertical line near the y-axis intersects all the horizontal lines and the curve at the point corresponding to y equals L – ε. Another dashed vertical line away from the y-axis intersects the horizontal lines at y equals L – ε and y equals L + ε and the curve at the point corresponding to y equals L + ε. The dashed horizontal line at y equals L extends downward vertically after intersecting the curve to reach the x-axis at x equals a. Double-sided arrows are marked on both sides of ‘a’ on the x-axis and are labeled ‘δ’, representing ‘x is within δ of a’. The vertical area corresponding to these arrows around ‘a’ is shaded up to y equals L + ε, while the horizontal area between y equals L – ε and y equals L + ε is shaded.

We now take a more analytical approach to establishing limits. Consult the figure on the right:

  • The symbol ε is the Greek letter epsilon.
  • The symbol δ is the Greek letter delta.
The idea illustrated here is that if the value of f open parentheses x close parentheses is within ε units of the limit L, then there is a corresponding value of δ such that x is within δ units of a.

Written as distances, we have the following:

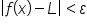
  • f open parentheses x close parentheses is within ε units of the limit L: open vertical bar f open parentheses x close parentheses minus L close vertical bar less than epsilon
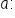
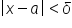
  • x is within δ units of a colon open vertical bar x minus a close vertical bar less than delta
These ideas are used to establish the Formal Definition of a Limit, which states:

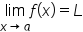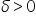limit as x rightwards arrow a of f open parentheses x close parentheses equals L means that for every given epsilon greater than 0 comma there exists delta greater than 0 so that:

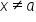  • If x is within δ units of a (and x not equal to a), then f open parentheses x close parentheses is within ε units of L.
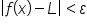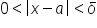  • This translates to open vertical bar f open parentheses x close parentheses minus L close vertical bar less than epsilon whenever 0 less than open vertical bar x minus a close vertical bar less than delta.
The goal in this part of the challenge will be to find the value of δ for a given value of ε.

hint
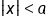You may recall from algebra that open vertical bar x close vertical bar less than a is equivalent to saying 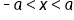short dash a less than x less than a for any positive number a.

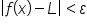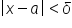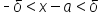This means that open vertical bar f open parentheses x close parentheses minus L close vertical bar less than epsilon can be rewritten short dash epsilon less than f open parentheses x close parentheses minus L less than epsilon and open vertical bar x minus a close vertical bar less than delta can be rewritten as short dash delta less than x minus a less than delta.

These ideas are useful in determining the value of δ for a given ε.

EXAMPLE

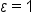Consider the limit statement: limit as x rightwards arrow 1 of open parentheses 5 x minus 2 close parentheses equals 3. What value of δ is required when epsilon equals 1?

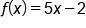Consider the picture shown below (the slanted line is the graph of f open parentheses x close parentheses equals 5 x minus 2):
A graph with an x-axis ranging from 0 to 1 and a y-axis ranging from 0 to 4. A line slants upward from the fourth quadrant to the first quadrant by passing through the x-axis between 0 and 1. Three horizontal dashed lines at y equals 2, y equals 3, and y equals 4 intersect the slanted line. The horizontal dashed line y equals 3 extends downward vertically after intersecting the slanted line to meet the x-axis at x equals 1. The area between y equals 2 and y equals 4 is shaded. The vertical area around x equals 1 is also shaded, extending up to y equals 4.
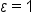Remember that epsilon equals 1 means that we desire f open parentheses x close parentheses to be within 1 unit of 3 (the limit). This means 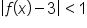open vertical bar f open parentheses x close parentheses minus 3 close vertical bar less than 1. Let’s solve this:

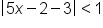
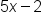open vertical bar 5 x minus 2 minus 3 close vertical bar less than 1 Replace f open parentheses x close parentheses with 5 x minus 2.
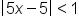
open vertical bar 5 x minus 5 close vertical bar less than 1 Simplify the expression.
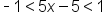
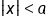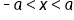short dash 1 less than 5 x minus 5 less than 1 open vertical bar x close vertical bar less than a means short dash a less than x less than a.
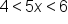
4 less than 5 x less than 6 Add 5 to all three parts.
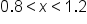
0.8 less than x less than 1.2 Divide all three parts by 5.

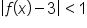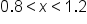Thus, open vertical bar f open parentheses x close parentheses minus 3 close vertical bar less than 1 implies that 0.8 less than x less than 1.2.

So, what is the value of δ?

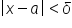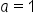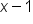Recall that the goal is to find δ so that open vertical bar x minus a close vertical bar less than delta. In this problem, a equals 1, so this can be written as open vertical bar x minus 1 close vertical bar less than delta.

Recall from algebra that this means short dash delta less than x minus 1 less than delta. Thus, it helps to get an inequality with x minus 1 in the middle. Then the left and right parts of the inequality give information as to what δ is.

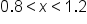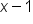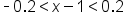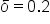We left off with 0.8 less than x less than 1.2. To get x minus 1 in the middle, subtract 1 from all parts of the inequality. This gives short dash 0.2 less than x minus 1 less than 0.2. Thus, delta equals 0.2.

In summary, we state the following: If x is within 0.2 units of 1, then f open parentheses x close parentheses is within 1 unit of 3.

While a graph is helpful, let’s try one now without the graph.

EXAMPLE

Consider the limit statement: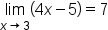 limit as x rightwards arrow 3 of open parentheses 4 x minus 5 close parentheses equals 7. Find the corresponding values of δ when ε 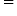equals 0.5, 0.1, and 0.01.

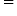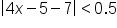For ε equals 0.5, this means we want open vertical bar 4 x minus 5 minus 7 close vertical bar less than 0.5. Now solve:

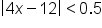
open vertical bar 4 x minus 12 close vertical bar less than 0.5 Simplify.
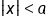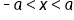short dash 0.5 less than 4 x minus 12 less than 0.5 open vertical bar x close vertical bar less than a means short dash a less than x less than a.
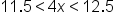
11.5 less than 4 x less than 12.5 Add 12 to all three parts.
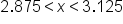
2.875 less than x less than 3.125 Divide all three parts by 4.
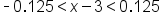
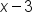short dash 0.125 less than x minus 3 less than 0.125 Subtract 3 from all three parts to get x minus 3 in the middle.

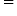Thus, δ equals 0.125.

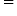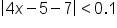For ε equals 0.1, this means we want open vertical bar 4 x minus 5 minus 7 close vertical bar less than 0.1. Now solve:

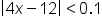
open vertical bar 4 x minus 12 close vertical bar less than 0.1 Simplify.
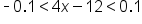
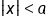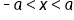short dash 0.1 less than 4 x minus 12 less than 0.1 open vertical bar x close vertical bar less than a means short dash a less than x less than a.
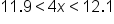
11.9 less than 4 x less than 12.1 Add 12 to all three parts.
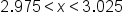
2.975 less than x less than 3.025 Divide all three parts by 4.
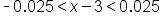
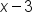short dash 0.025 less than x minus 3 less than 0.025 Subtract 3 from all three parts to get x minus 3 in the middle.

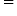Thus, δ equals 0.025.

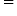For ε equals 0.01, this means we want 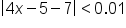open vertical bar 4 x minus 5 minus 7 close vertical bar less than 0.01. Now solve:

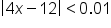
open vertical bar 4 x minus 12 close vertical bar less than 0.01 Simplify.
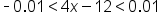
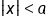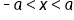short dash 0.01 less than 4 x minus 12 less than 0.01 open vertical bar x close vertical bar less than a means short dash a less than x less than a.
11.99 less than 4 x less than 12.01 Add 12 to all three parts.
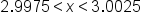
2.9975 less than x less than 3.0025 Divide all three parts by 4.
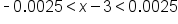
short dash 0.0025 less than x minus 3 less than 0.0025 Subtract 3 from all three parts to get 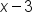x minus 3 in the middle.

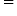Thus, δ equals 0.0025.

hint
Note that as the value of ε gets smaller, so does δ. This is the essence of a limit. As one distance gets smaller, the other does as well.

big idea
As the chosen values of ε get closer to 0, the corresponding value of δ also gets closer to 0.

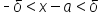When f open parentheses x close parentheses is a linear function, finding the value of δ is fairly straightforward since the final inequality always has the form short dash delta less than x minus a less than delta.

When f open parentheses x close parentheses is a nonlinear function, this may not be the case, which means we have to think more critically to get the appropriate value of δ.

term to know
Formal Definition of a Limit
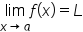limit as x rightwards arrow a of f open parentheses x close parentheses equals L means that for every given ε > 0, there exists δ > 0 so that:
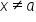  • If x is within δ units of a (and x not equal to a), then f open parentheses x close parentheses is within ε units of L.
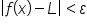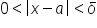  • This translates to open vertical bar f open parentheses x close parentheses minus L close vertical bar less than epsilon whenever 0 less than open vertical bar x minus a close vertical bar less than delta.

2. Finding the Value of δ That Corresponds to a Given Value of ε for a Nonlinear Function

The following are inequalities that may be useful. In each case, assume that c and d are nonnegative numbers.

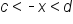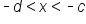  • If c less than short dash x less than d, then short dash d less than x less than short dash c.
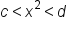  • If c less than x squared less than d, then 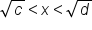square root of c less than x less than square root of d (assuming x is positive).
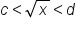  • If c less than square root of x less than d, then c squared less than x less than d squared.
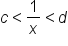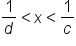  • If c less than 1 over x less than d, then 1 over d less than x less than 1 over c.

EXAMPLE

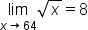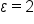Consider the limit statement: limit as x rightwards arrow 64 of square root of x equals 8. Let’s find the corresponding value of δ when epsilon equals 2.

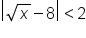We want open vertical bar square root of x minus 8 close vertical bar less than 2.

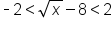
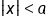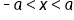short dash 2 less than square root of x minus 8 less than 2 open vertical bar x close vertical bar less than a means short dash a less than x less than a.
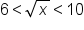
6 less than square root of x less than 10 Add 8 to all three parts.
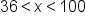
36 less than x less than 100 Square all parts of the inequality.
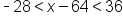
short dash 28 less than x minus 64 less than 36 Subtract 64 from all three parts to get 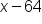x minus 64 in the middle.

Notice that this inequality is not “balanced.” This makes it unclear what to select for δ. Is the answer 28 or 36? Remember what we are trying to say:

In order for f open parentheses x close parentheses to be within 2 units of 8, x has to be within _____ units of 64.

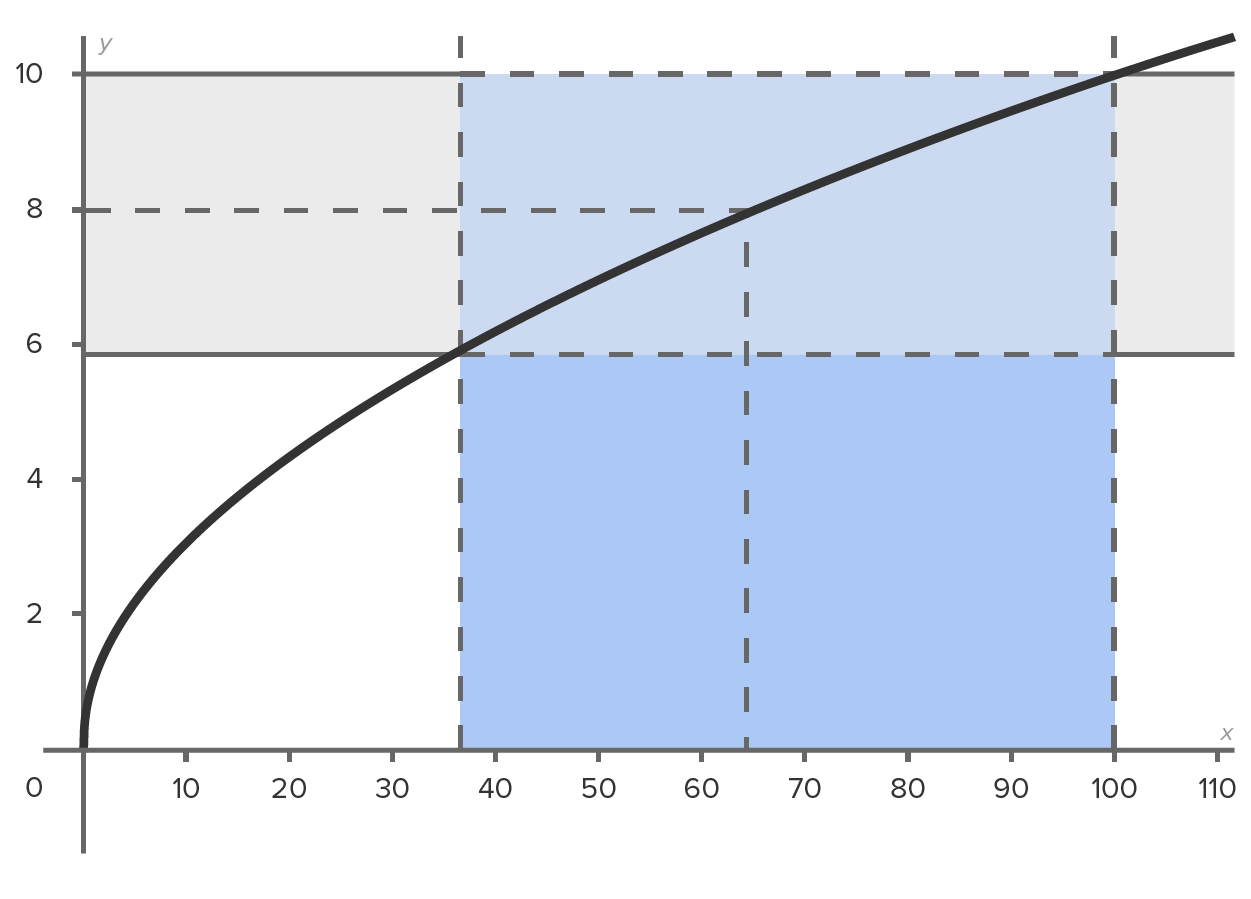Consider the graph shown to the right:
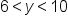  • The horizontal band shows that 6 less than y less than 10.
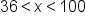  • The vertical band shows that 36 less than x less than 100.
The intersection is the “area of interest” for the limit.

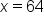If we move 28 units away from x equals 64 in either direction, we stay inside the vertical band, which guarantees that f open parentheses x close parentheses is within 2 units of the limit.

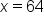If we move 36 units away from x equals 64 in either direction, we could fall outside the vertical band on the left-hand side, which does not guarantee that f open parentheses x close parentheses is within 2 units of the limit.

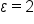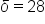To guarantee that f open parentheses x close parentheses is within 2 units of the limit (8), x needs to be within 28 units of 64. Thus, when epsilon equals 2, delta equals 28.

watch
The following video provides an example for a linear function and a radical function.

try it
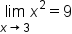Consider the limit statement limit as x rightwards arrow 3 of x squared equals 9.

Find the value of δ that corresponds to ε = 0.5. Round δ to the nearest hundredth.
We want 8.5 less than x squared less than 9.5, which means 2.915 less than x less than 3.082, which in turn means short dash 0.085 less than x minus 3 less than 0.082. To find δ, compare open vertical bar short dash 0.085 close vertical bar and open vertical bar 0.082 close vertical bar since we are examining the distances between x and 3. Since 0.082 less than 0.085, use delta equals 0.082.

EXAMPLE

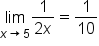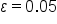Consider the limit statement: limit as x rightwards arrow 5 of fraction numerator 1 over denominator 2 x end fraction equals 1 over 10. Let’s find δ when epsilon equals 0.05.

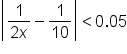Start with open vertical bar fraction numerator 1 over denominator 2 x end fraction minus 1 over 10 close vertical bar less than 0.05.

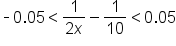
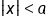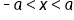short dash 0.05 less than fraction numerator 1 over denominator 2 x end fraction minus 1 over 10 less than 0.05 open vertical bar x close vertical bar less than a means short dash a less than x less than a.
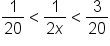
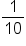1 over 20 less than fraction numerator 1 over denominator 2 x end fraction less than 3 over 20 Add 1 over 10, and convert all to fractions.
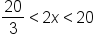
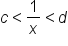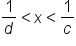20 over 3 less than 2 x less than 20 c less than 1 over x less than d means 1 over d less than x less than 1 over c.
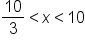
10 over 3 less than x less than 10 Divide by 2.
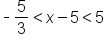
short dash 5 over 3 less than x minus 5 less than 5 Subtract 5.

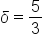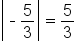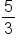It follows that delta equals 5 over 3 since open vertical bar short dash 5 over 3 close vertical bar equals 5 over 3 and 5 over 3 is smaller than 5.

summary
In this lesson, you learned that by using the formal definition of a limit, you can observe the relationship between ε and δ, which emphasizes the idea of “f open parentheses x close parentheses getting closer to the limit as x gets closer to a.” In this challenge, the goal was to find the value of δ that corresponds to a given value of ε for a linear function and a nonlinear function, and we observed that one getting smaller causes the other to get smaller. For linear functions, identifying δ is rather straightforward, but for nonlinear functions, more critical thinking is required to find the appropriate value of δ.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 1 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Formal Definition of a Limit

limit as x rightwards arrow a of f open parentheses x close parentheses equals L means that for every given ε > 0, there exists δ > 0 so that:

• If x is within δ units of a (and x not equal to a), then f open parentheses x close parentheses is within ε units of L.
• This translates to open vertical bar f open parentheses x close parentheses minus L close vertical bar less than epsilon whenever 0 less than open vertical bar x minus a close vertical bar less than delta.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.