Table of Contents |
A hyperbola is obtained by cutting a plane through a double cone, as shown in the figure.

The graph of a hyperbola with center 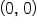 and vertices along the horizontal axis is shown below.
and vertices along the horizontal axis is shown below.
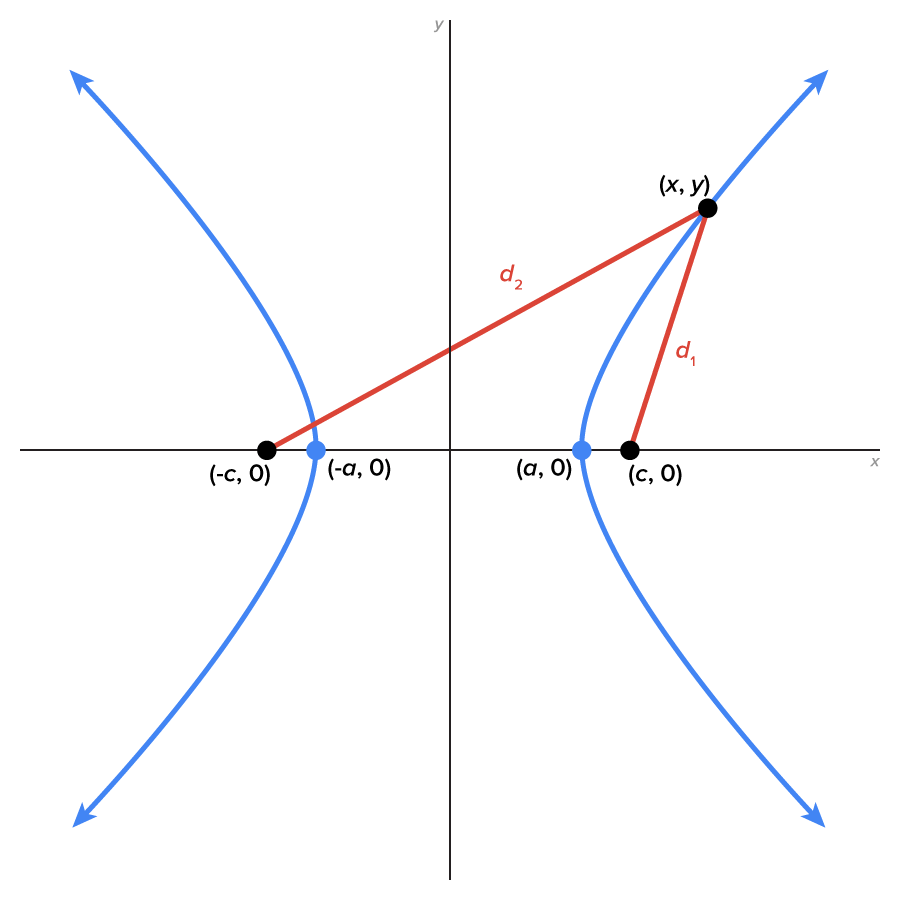
A hyperbola is defined as the set of all points 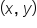 such that the absolute difference between the distances from
such that the absolute difference between the distances from 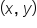 to each focus is constant. That is,
to each focus is constant. That is, 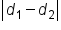 is constant.
is constant.
Considering this definition with both horizontal and vertical axes, there are two possible basic graphs and equations of hyperbolas when centered at the origin, as shown below.
| Graph 1 | Graph 2 |
|---|---|
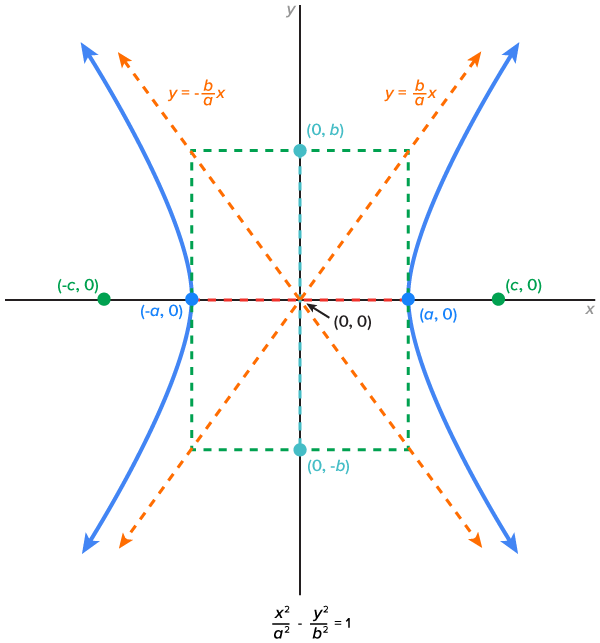 Vertices: 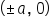 Foci: 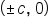 Asymptotes: 
|
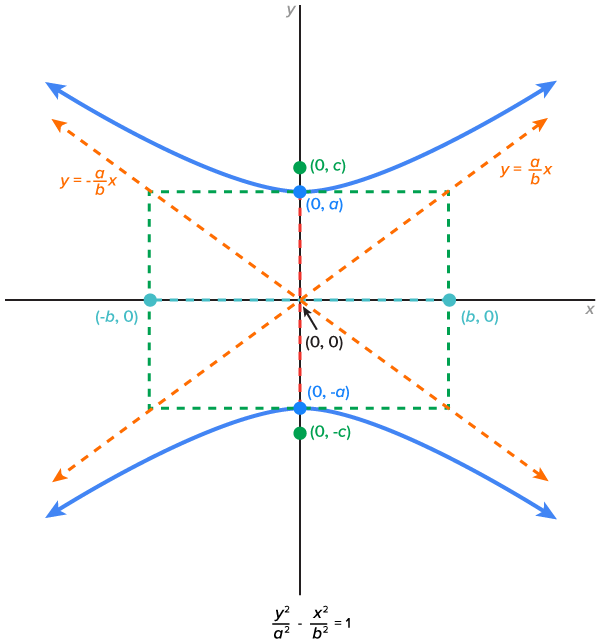 Vertices: 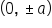 Foci: 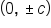 Asymptotes: 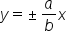
|
Note the following:
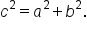
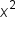 term has a positive coefficient, the vertices and foci are along the x-axis.
term has a positive coefficient, the vertices and foci are along the x-axis.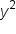 term has a positive coefficient, the vertices and foci are along the y-axis.
term has a positive coefficient, the vertices and foci are along the y-axis.EXAMPLE
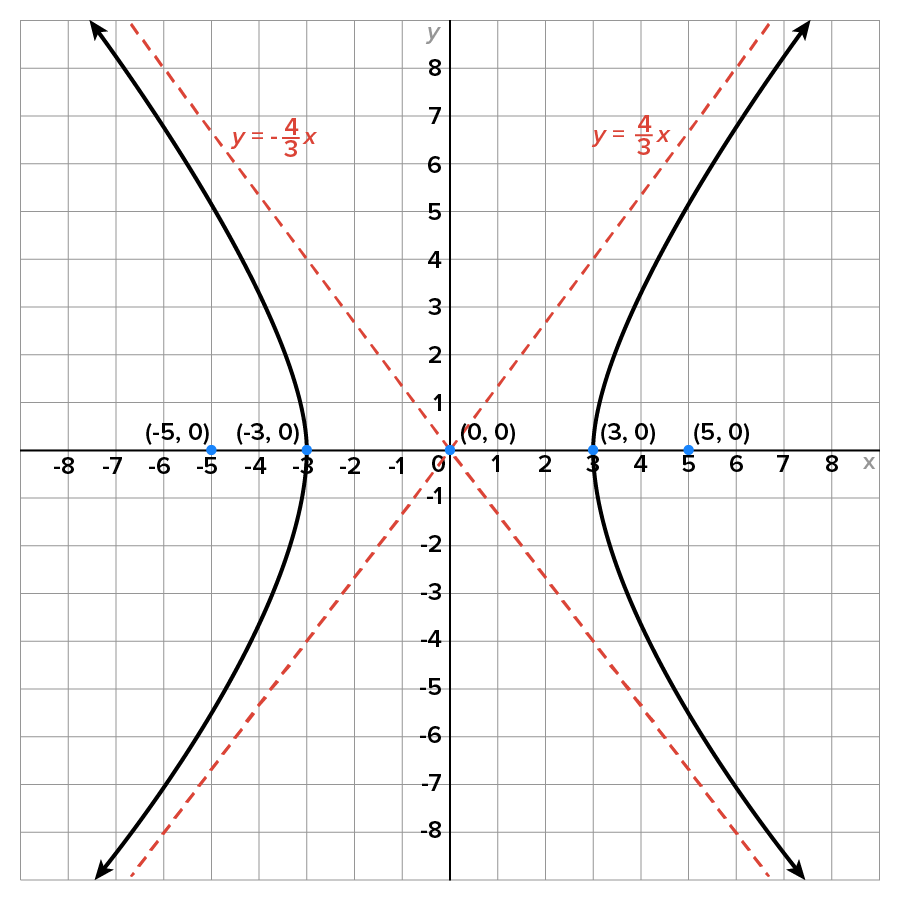
Consider the hyperbola whose equation is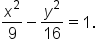
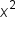 term has a positive coefficient, this matches to the equation
term has a positive coefficient, this matches to the equation 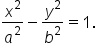
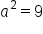 and
and 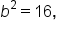 which means
which means 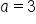 and
and 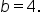
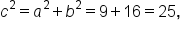 which gives
which gives 
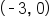 and
and 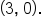
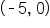 and
and 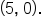
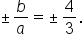 Therefore, the equations of the asymptotes are
Therefore, the equations of the asymptotes are 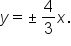
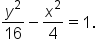
Similar to ellipses, hyperbolas can look very different from one another in terms of how wide or narrow they open. The following figures below show hyperbolas, each with a horizontal major axis. Note that the vertices of each hyperbola are 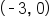 and
and 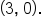
| Equation | Figure |
|---|---|

|
Figure 1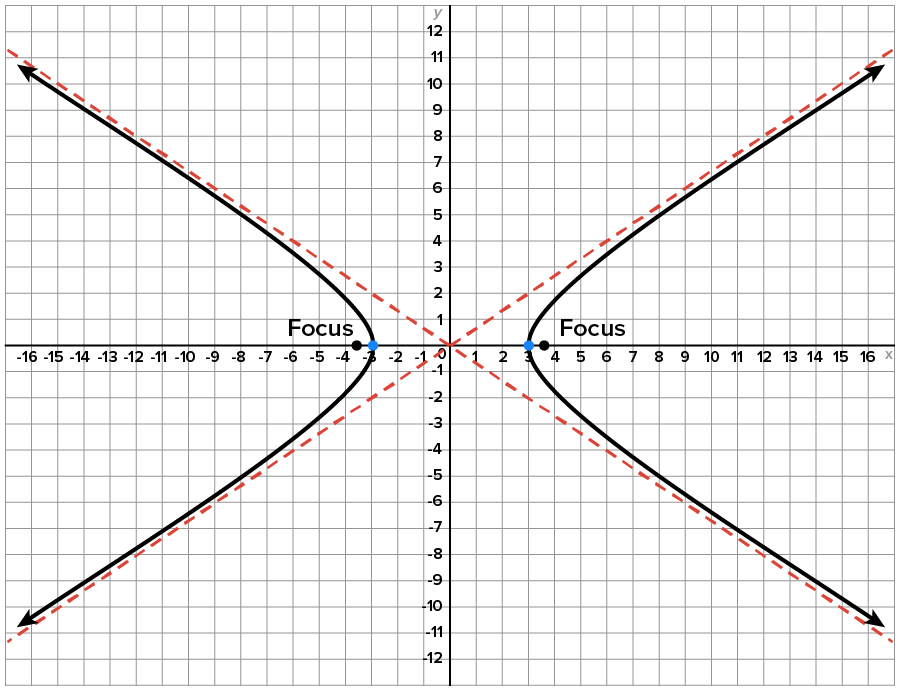
|
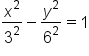
|
Figure 2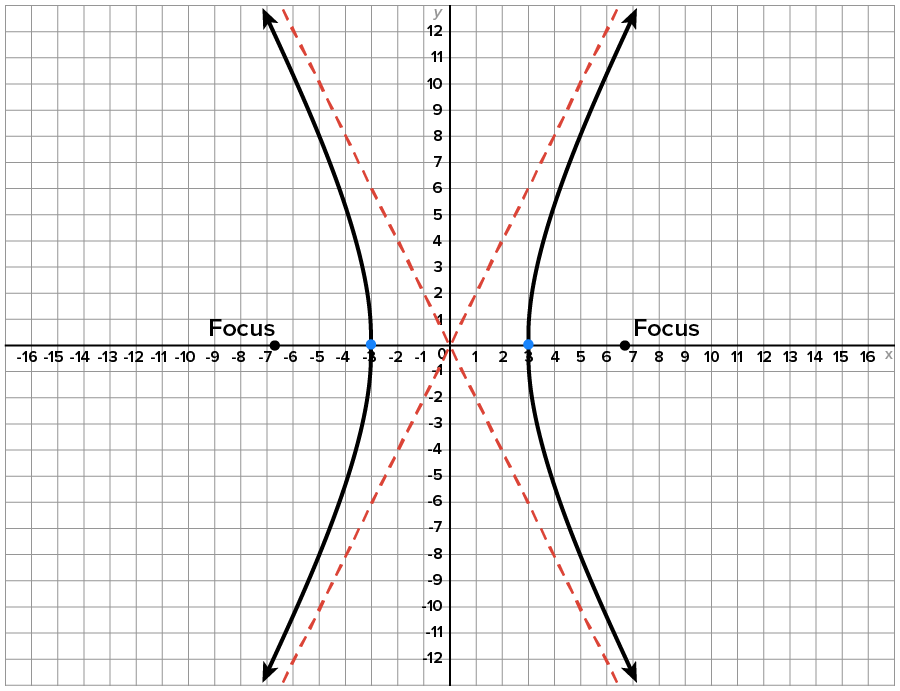
|
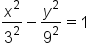
|
Figure 3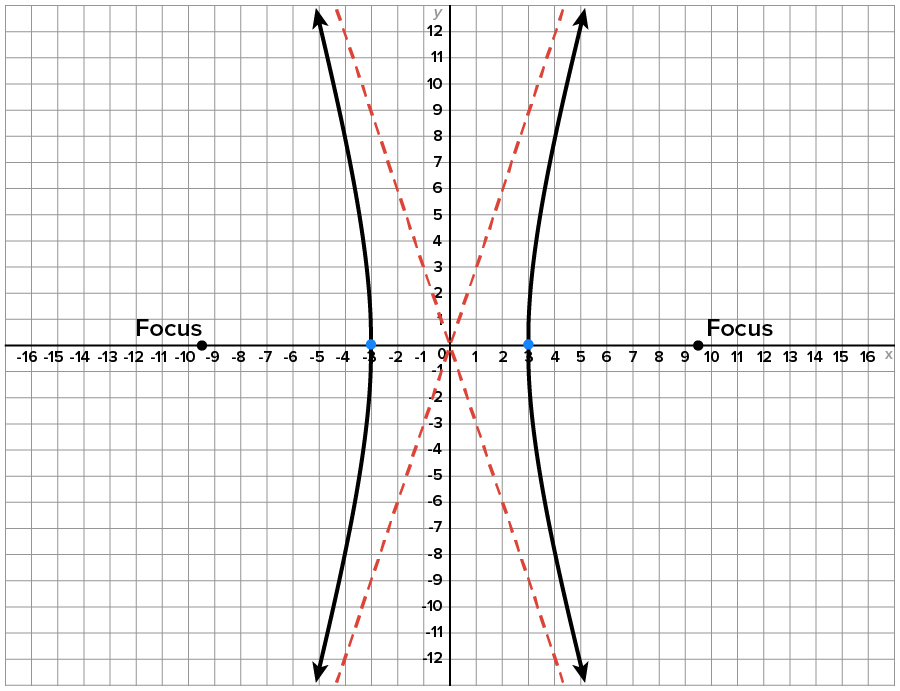
|
Even though each is classified as a hyperbola, they look very different. Figure 1 has a very narrow opening in the horizontal direction compared to the others, while Figure 3 has the widest opening in the horizontal direction compared to the others. Notice that the wider the opening, the further the foci are from the center.
Eccentricity can also be used to distinguish hyperbolas from each other in terms of how narrow or wide their openings are. The formula for eccentricity as it applies to hyperbolas is the same as before: 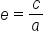
For any hyperbola,  since the foci are further away from the center than the vertices are. Also, since
since the foci are further away from the center than the vertices are. Also, since 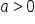 and
and 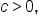 it follows that every hyperbola has eccentricity
it follows that every hyperbola has eccentricity 
EXAMPLE
From the three hyperbolas given above, we find their eccentricities as follows:| Equation | Find the Value of c |
Eccentricity 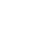
|
|---|---|---|
Figure 1 
|
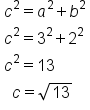
|
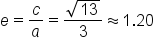
|
Figure 2 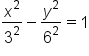
|

|
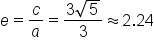
|
Figure 3 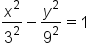
|
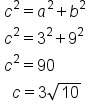
|

|
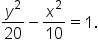
When the center is located at 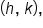 the graphs and equations are as follows:
the graphs and equations are as follows:
| Graph 1 | Graph 2 |
|---|---|
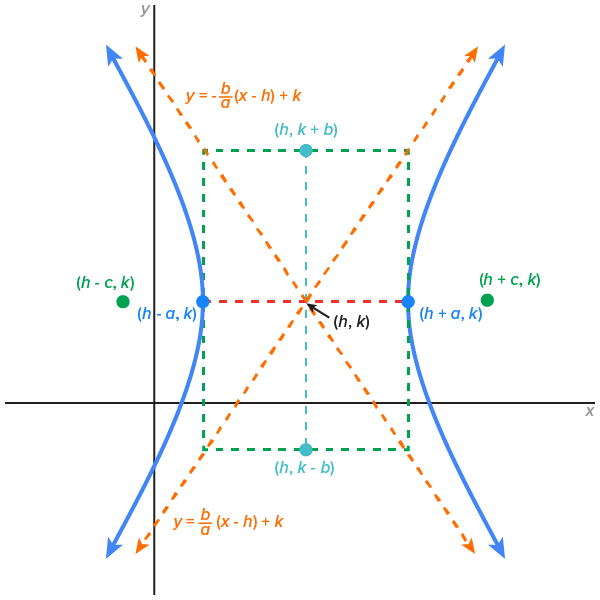  Vertices: 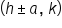 Foci: 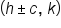 Asymptotes: 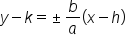
|
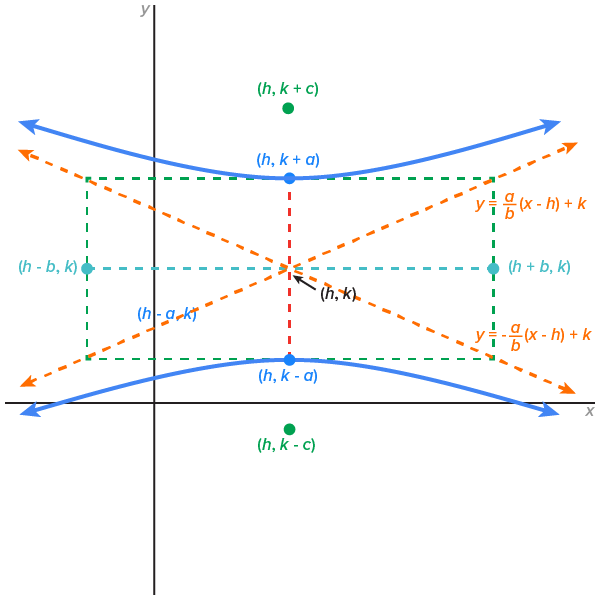  Vertices:  Foci: 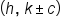 Asymptotes: 
|
Note the following:
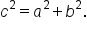
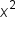 term has a positive coefficient, the transverse axis is parallel to the x-axis.
term has a positive coefficient, the transverse axis is parallel to the x-axis. 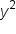 term has a positive coefficient, the transverse axis is parallel to the y-axis.
term has a positive coefficient, the transverse axis is parallel to the y-axis. 
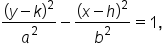 where
where 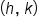 is the center.
is the center. 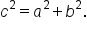
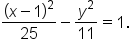
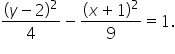
EXAMPLE
Consider the equation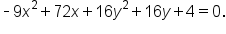

|
This is the original equation. |
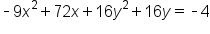
|
Subtract 4 from both sides so all the variable terms are on one side and the constant is on the other side. |
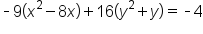
|
Factor out -9 from the x-terms and 16 from the y-terms. |
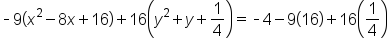
|
Add 16 to complete the square for  This means that This means that 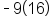 is added to the left side; therefore, add is added to the left side; therefore, add 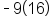 to the right side as well. to the right side as well. Add 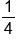 to complete the square for to complete the square for 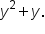 This means that This means that 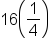 is added to the left side; therefore, add is added to the left side; therefore, add 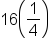 to the right side as well. to the right side as well.
|
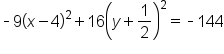
|
Rewrite the quadratic terms as perfect squares on the left side, and simplify the right side. |
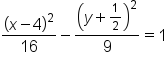
|
Divide both sides by -144. |
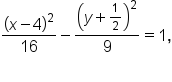 which makes it a hyperbola with center at
which makes it a hyperbola with center at  Now that this equation is in standard form, other characteristics like the vertices, foci, and asymptotes can also be identified.
Now that this equation is in standard form, other characteristics like the vertices, foci, and asymptotes can also be identified.
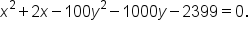
Given information about the various graphical aspects of a hyperbola, we can write the equation of said hyperbola.
EXAMPLE
A hyperbola has foci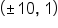 and vertices
and vertices 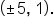 What is the equation of the hyperbola?
What is the equation of the hyperbola?
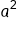 and
and 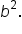
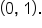
 is used.
is used.
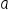 and b :
and b :
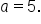
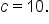
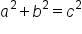 to find
to find 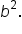
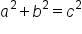
|
This is the equation that relates 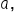 b, and c. b, and c.
|
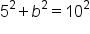
|
Substitute 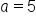 and and 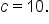
|
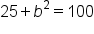
|
Simplify. |
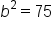
|
Solve for 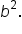
|
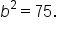 Then, substituting
Then, substituting 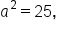
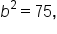 and
and 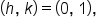 the equation of the hyperbola is
the equation of the hyperbola is 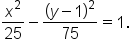
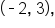 a vertex at
a vertex at 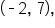 and a focus at
and a focus at 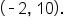
EXAMPLE
A hyperbola has its center at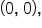 a focus at
a focus at 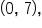 and eccentricity
and eccentricity  Write the equation of the hyperbola in standard form.
Write the equation of the hyperbola in standard form.
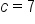
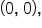 this also means that the equation of the hyperbola has the form
this also means that the equation of the hyperbola has the form 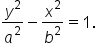
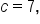 so we will need to use the given eccentricity to find
so we will need to use the given eccentricity to find 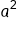 and
and 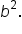
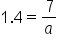
|
Use the eccentricity formula 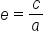 with with  and and 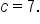
|
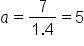
|
Solve for 
|
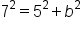
|
Next, use the formula 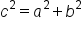 with with 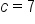 and and 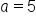 to find to find 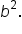
|
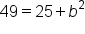
|
Simplify. |

|
Solve for 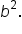
|
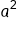 with 25 and
with 25 and 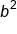 with 24, the equation of the ellipse is
with 24, the equation of the ellipse is 
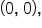 a vertex at
a vertex at 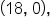 and eccentricity
and eccentricity 
Hyperbolas are used to model several real-world applications.
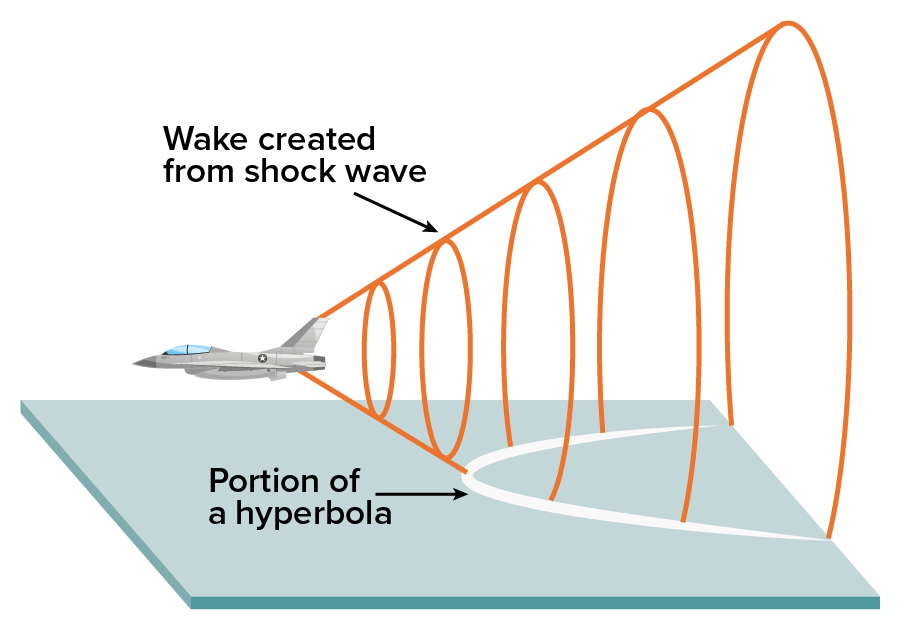
 and at its closest points is 5 feet from the fountain.
and at its closest points is 5 feet from the fountain.
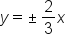 and is 12 feet from the fountain at its closest points.
and is 12 feet from the fountain at its closest points.
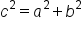 , and transverse axis, and you explored these graphical aspects of a hyperbola with center at the origin and with center not at the origin. You also learned that given a hyperbola's equation, you can analyze these characteristics. In addition, given information about a hyperbola, notably the coordinates of its center, its transverse axis, and the values of
, and transverse axis, and you explored these graphical aspects of a hyperbola with center at the origin and with center not at the origin. You also learned that given a hyperbola's equation, you can analyze these characteristics. In addition, given information about a hyperbola, notably the coordinates of its center, its transverse axis, and the values of 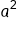 and
and 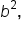 you can write the equation of a hyperbola, which is very useful in solving applied problems that involve hyperbolas.
you can write the equation of a hyperbola, which is very useful in solving applied problems that involve hyperbolas.
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.