Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

The Graph Method

Author: Sophia
PDF Version

what's covered
In this lesson, you will evaluate limits by using the graph of a function. Specifically, this lesson will cover:

Table of Contents

1. Defining Limit Notation

Consider the function 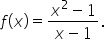f open parentheses x close parentheses equals fraction numerator x squared minus 1 over denominator x minus 1 end fraction.

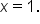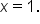Notice that f open parentheses x close parentheses is undefined when x equals 1. However, we still may want to analyze the behavior of f open parentheses x close parentheses around x equals 1. The mathematical tool used to do this sort of analysis is called a limit.

big idea
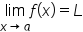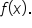
limit as x rightwards arrow a of f open parentheses x close parentheses equals L means “the limit of f open parentheses x close parentheses as x gets closer to a is equal to L”. In other words, as x gets closer to a, the value of f open parentheses x close parentheses gets closer to L. We call L the limit of the function f open parentheses x close parentheses.

To see how this works graphically, shown below is the graph of 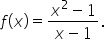f open parentheses x close parentheses equals fraction numerator x squared minus 1 over denominator x minus 1 end fraction.

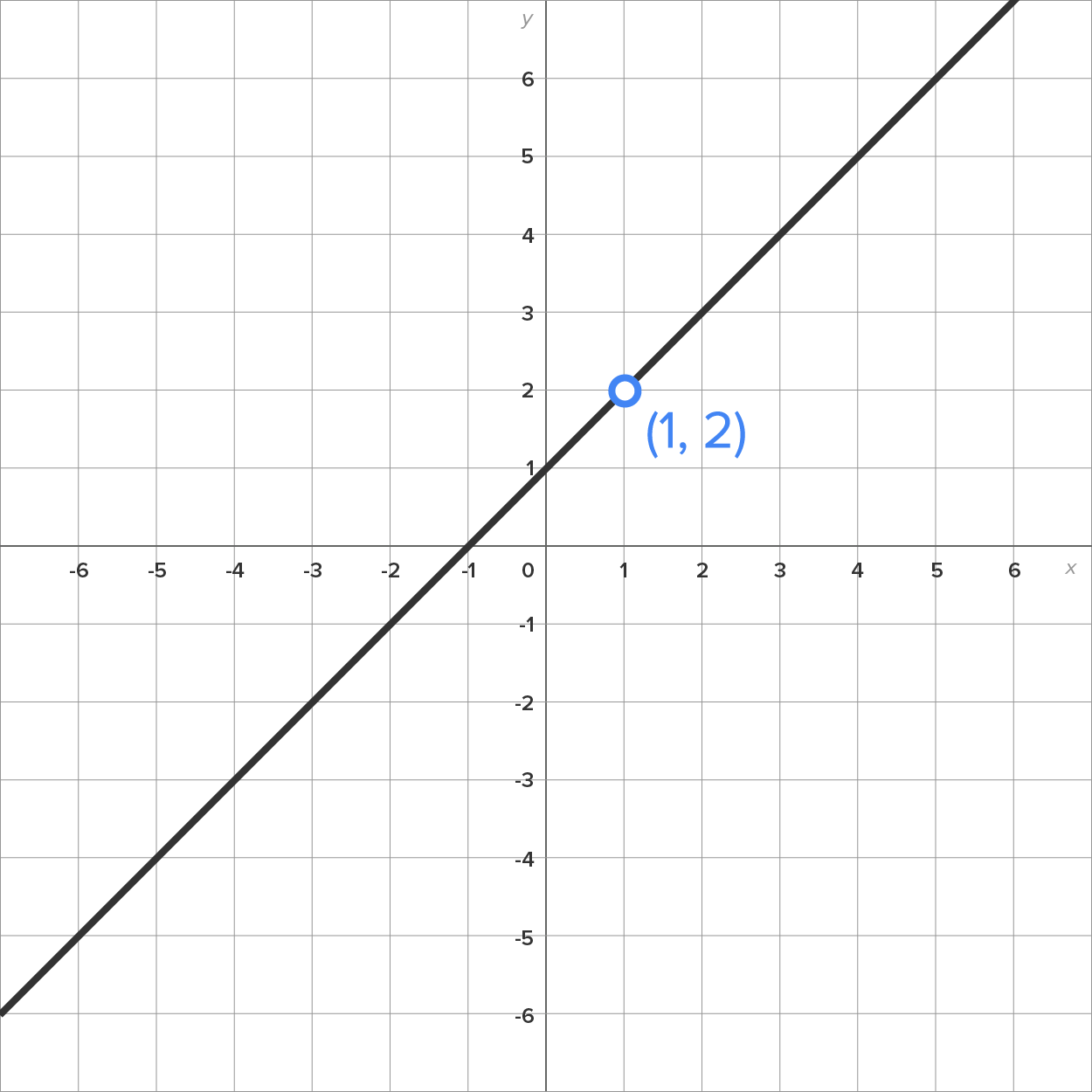
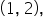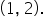
Notice that there is a hole in the graph at the point open parentheses 1 comma space 2 close parentheses comma indicating that the graph of f open parentheses x close parentheses is a line, but excludes the point open parentheses 1 comma space 2 close parentheses.

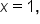Since f open parentheses x close parentheses is undefined when x equals 1 comma we analyze the behavior of f open parentheses x close parentheses by using limits.

That is, we want to evaluate 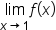limit as x rightwards arrow 1 of f open parentheses x close parentheses or more specifically,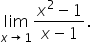 limit as x rightwards arrow 1 of fraction numerator x squared minus 1 over denominator x minus 1 end fraction.

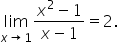
By examining the graph, it appears that as x gets closer and closer to 1, f open parentheses x close parentheses gets closer and closer to 2. Thus, we can write limit as x rightwards arrow 1 of fraction numerator x squared minus 1 over denominator x minus 1 end fraction equals 2.

term to know
Limit
The value that a function f open parentheses x close parentheses approaches as x gets closer to a specified number.

2. Using Graphs to Evaluate Limits

We can use the information from a graph to evaluate a limit.

EXAMPLE

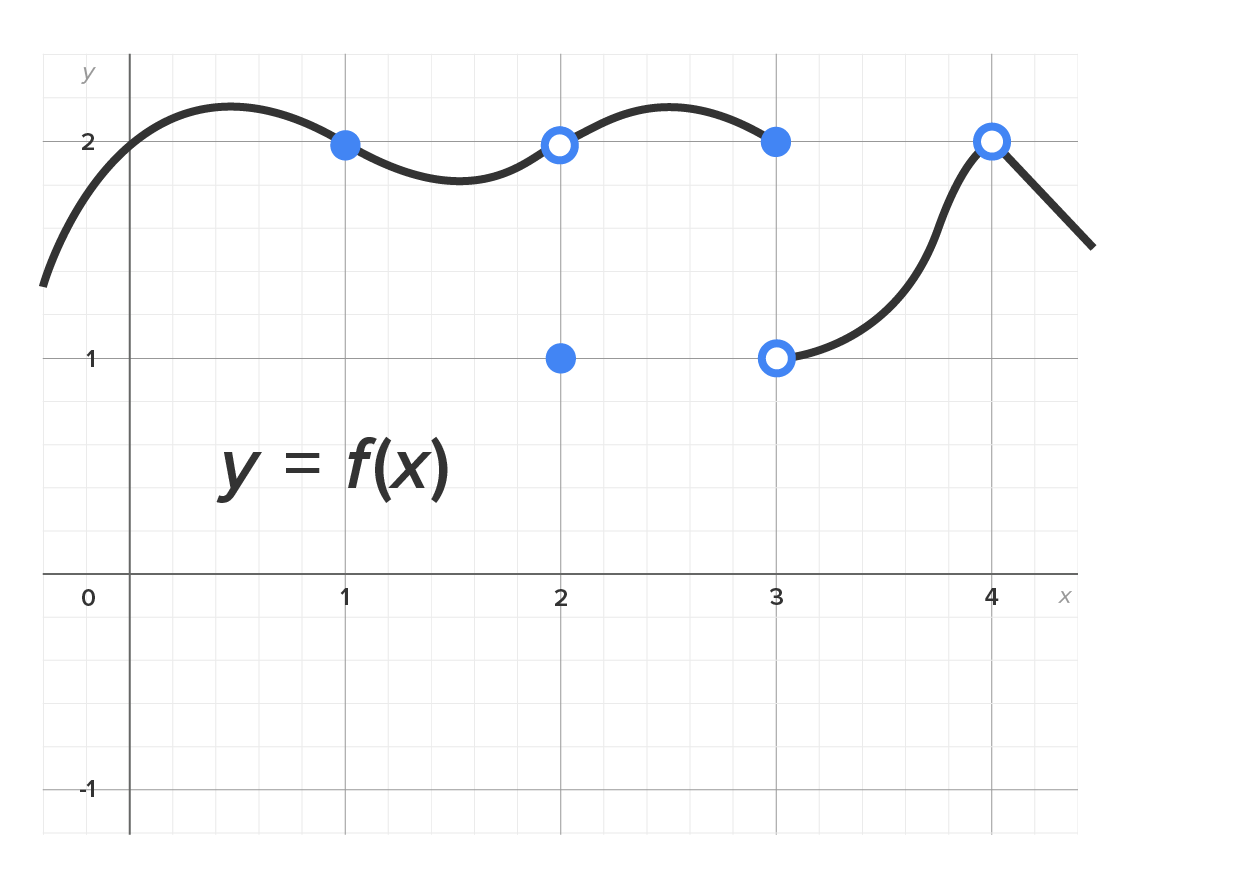
Consider the graph of some function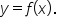 y equals f open parentheses x close parentheses.

We can say the following:

Statement Description
limit as x rightwards arrow 0 of f open parentheses x close parentheses equals 1 As x gets closer to 0, f open parentheses x close parentheses gets closer to 1.
limit as x rightwards arrow 1 of f open parentheses x close parentheses equals 1 As x gets closer to 1, f open parentheses x close parentheses gets closer to 1.
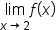limit as x rightwards arrow 2 of f open parentheses x close parentheses does not exist. As x gets closer to 2 from the left (values smaller than 2), f open parentheses x close parentheses gets closer to 1. However, as x gets closer to 2 from the right (values larger than 2), f open parentheses x close parentheses gets closer to 2.

Since f open parentheses x close parentheses approaches two different values, as x approaches 2, we say the limit does not exist.
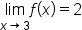
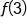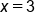limit as x rightwards arrow 3 of f open parentheses x close parentheses equals 2 As x gets closer to 3, f open parentheses x close parentheses gets closer to 2. Note that the actual value of f open parentheses 3 close parentheses is 1 (closed dot at x equals 3), but the limit tells us what is happening as we get closer and closer to 3, not what is happening right at 3.
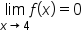
limit as x rightwards arrow 4 of f open parentheses x close parentheses equals 0 As x gets closer to 4, f open parentheses x close parentheses gets closer to 0.

try it
Consider the graph pictured below.



Evaluate the function as x approaches 1.
limit as x rightwards arrow 1 of f open parentheses x close parentheses equals 2
Evaluate the function as x approaches 2.
limit as x rightwards arrow 2 of f open parentheses x close parentheses equals 2
Evaluate the function as x approaches 3.
limit as x rightwards arrow 3 of f open parentheses x close parentheses does not exist
Evaluate the function as x approaches 4.
limit as x rightwards arrow 4 of f open parentheses x close parentheses equals 2

summary
In this lesson, you learned about defining limit notation, or how the limit of a function is used to determine the behavior (or value) a function f open parentheses x close parentheses approaches as x gets closer to some value. You also learned that you can use the information from a graph to evaluate a limit.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 1 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Limit

The value that a function f open parentheses x close parentheses approaches as x gets closer to a specified number.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.