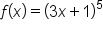Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

The General Power Rule for Functions

Author: Sophia
PDF Version

what's covered
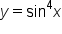In this lesson, you will expand upon your derivative knowledge even further by examining powers of functions whose derivatives we know. For example, f open parentheses x close parentheses equals open parentheses 3 x plus 1 close parentheses to the power of 5 and y equals sin to the power of 4 x. This idea will also help in finding the derivatives of some other commonly used functions. Specifically, this lesson will cover:

Table of Contents

1. Derivatives of Functions of the Form y = [f  (x)]n

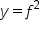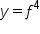Derivatives of powers of a function have several uses, as we will see once we get to applications of derivatives. To establish a pattern for this type of derivative, we’ll consider the functions y equals f squared, y equals f cubed, and y equals f to the power of 4, where f is being used to represent some function f open parentheses x close parentheses.

First, consider the function 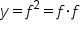y equals f squared equals f times f.

By the product rule, we have:

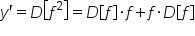
y apostrophe equals D open square brackets f squared close square brackets equals D open square brackets f close square brackets times f plus f times D open square brackets f close square brackets
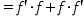
equals f apostrophe times f plus f times f apostrophe
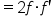
equals 2 f times f apostrophe


Now consider the function 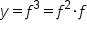y equals f cubed equals f squared times f.

By the product rule again, we have:

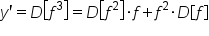
y apostrophe equals D open square brackets f cubed close square brackets equals D open square brackets f squared close square brackets times f plus f squared times D open square brackets f close square brackets Apply the product rule.
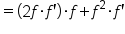
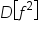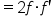equals open parentheses 2 f times f apostrophe close parentheses times f plus f squared times f apostrophe Replace D open square brackets f squared close square brackets with equals 2 f times f apostrophe.
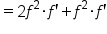
equals 2 f squared times f apostrophe plus f squared times f apostrophe Combine f times f equals f squared.
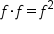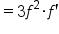
equals 3 f squared times f apostrophe Combine like terms.

Next, consider 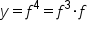y equals f to the power of 4 equals f cubed times f.

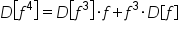
D open square brackets f to the power of 4 close square brackets equals D open square brackets f cubed close square brackets times f plus f cubed times D open square brackets f close square brackets Apply the product rule.
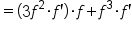
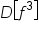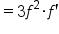equals open parentheses 3 f squared times f apostrophe close parentheses times f plus f cubed times f apostrophe Replace D open square brackets f cubed close square brackets with equals 3 f squared times f apostrophe.
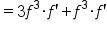
equals 3 f cubed times f apostrophe plus f cubed times f apostrophe Combine f squared times f equals f cubed.
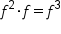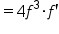
equals 4 f cubed times f apostrophe Combine like terms.

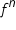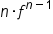By looking at this pattern, it seems as though the derivative of f to the power of n is n times f to the power of n minus 1 end exponent (looks like the power rule), but then also multiplied by f apostrophe.

formula to know
General Power Rule for Derivatives of Functions
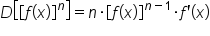If f open parentheses x close parentheses is some function, then D open square brackets open square brackets f open parentheses x close parentheses close square brackets to the power of n close square brackets equals n times open square brackets f open parentheses x close parentheses close square brackets to the power of n minus 1 end exponent times f apostrophe open parentheses x close parentheses.

EXAMPLE

Earlier, we found the derivative of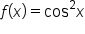 f open parentheses x close parentheses equals cos squared x by using the product rule. Let’s use the power rule and compare.

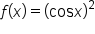First, note that this can be written as f open parentheses x close parentheses equals open parentheses cos x close parentheses squared.

By the power rule, we have the following:

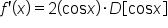
f apostrophe open parentheses x close parentheses equals 2 open parentheses cos x close parentheses times D open square brackets cos x close square brackets Apply the power rule.
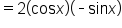
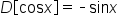
equals 2 open parentheses cos x close parentheses open parentheses short dash sin x close parentheses D open square brackets cos x close square brackets equals short dash sin x
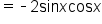
equals short dash 2 sin x cos x Combine and eliminate parentheses.

This matches the answer obtained in challenge 3.2.4.

EXAMPLE

Find the derivative of the function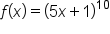 f open parentheses x close parentheses equals open parentheses 5 x plus 1 close parentheses to the power of 10.

By the power rule, we have the following:

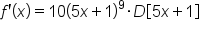
f apostrophe open parentheses x close parentheses equals 10 open parentheses 5 x plus 1 close parentheses to the power of 9 times D open square brackets 5 x plus 1 close square brackets Apply the power rule.
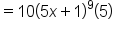
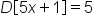
equals 10 open parentheses 5 x plus 1 close parentheses to the power of 9 open parentheses 5 close parentheses D open square brackets 5 x plus 1 close square brackets equals 5
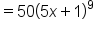
equals 50 open parentheses 5 x plus 1 close parentheses to the power of 9 Combine 10 times 5.

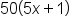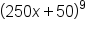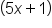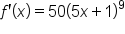A common mistake to make here is to multiply 50 open parentheses 5 x plus 1 close parentheses to get 250x + 50, and subsequently open parentheses 250 x plus 50 close parentheses to the power of 9. This is not correct since the open parentheses 5 x plus 1 close parentheses is raised to the 9th power and the 50 is not; therefore, they cannot be combined this way. The final answer is f apostrophe open parentheses x close parentheses equals 50 open parentheses 5 x plus 1 close parentheses to the power of 9.

try it
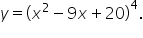
Consider the function y equals open parentheses x squared minus 9 x plus 20 close parentheses to the power of 4.
Find the derivative.
The function is in the form y equals open square brackets f open parentheses x close parentheses close square brackets to the power of 4 comma where f open parentheses x close parentheses equals x squared minus 9 x plus 20.

Then, by the general power rule, the derivative of y is fraction numerator d y over denominator d x end fraction equals 4 open square brackets f open parentheses x close parentheses close square brackets cubed times f apostrophe open parentheses x close parentheses.

Since f apostrophe open parentheses x close parentheses equals 2 x minus 9 comma we have fraction numerator d y over denominator d x end fraction equals 4 open parentheses x squared minus 9 x plus 20 close parentheses cubed open parentheses 2 x minus 9 close parentheses.

Rearranging factors, this can also be written fraction numerator d y over denominator d x end fraction equals 4 open parentheses 2 x minus 9 close parentheses open parentheses x squared minus 9 x plus 20 close parentheses cubed.

Remember the other expressions that can be written as powers of x.

EXAMPLE

Find the derivative of the function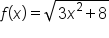 f open parentheses x close parentheses equals square root of 3 x squared plus 8 end root.

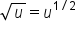Remember that square root of u equals u to the power of 1 divided by 2 end exponent. Then the power rule can be used.

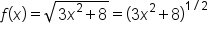
f open parentheses x close parentheses equals square root of 3 x squared plus 8 end root equals open parentheses 3 x squared plus 8 close parentheses to the power of 1 divided by 2 end exponent Rewrite the radical using a power.
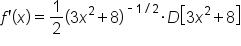
f apostrophe open parentheses x close parentheses equals 1 half open parentheses 3 x squared plus 8 close parentheses to the power of short dash 1 divided by 2 end exponent times D open square brackets 3 x squared plus 8 close square brackets Use the power rule for derivatives.
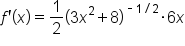
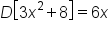
f apostrophe open parentheses x close parentheses equals 1 half open parentheses 3 x squared plus 8 close parentheses to the power of short dash 1 divided by 2 end exponent times 6 x D open square brackets 3 x squared plus 8 close square brackets equals 6 x
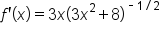
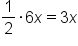
f apostrophe open parentheses x close parentheses equals 3 x open parentheses 3 x squared plus 8 close parentheses to the power of short dash 1 divided by 2 end exponent 1 half times 6 x equals 3 x
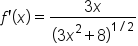
f apostrophe open parentheses x close parentheses equals fraction numerator 3 x over denominator open parentheses 3 x squared plus 8 close parentheses to the power of 1 divided by 2 end exponent end fraction Rewrite with nonnegative exponents.

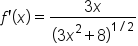Thus, f apostrophe open parentheses x close parentheses equals fraction numerator 3 x over denominator open parentheses 3 x squared plus 8 close parentheses to the power of 1 divided by 2 end exponent end fraction, which could also be written 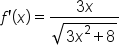f apostrophe open parentheses x close parentheses equals fraction numerator 3 x over denominator square root of 3 x squared plus 8 end root end fraction if radical notation is desired.

EXAMPLE

Find the derivative of the function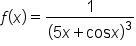 f open parentheses x close parentheses equals 1 over open parentheses 5 x plus cos x close parentheses cubed.

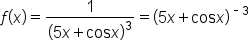
f open parentheses x close parentheses equals 1 over open parentheses 5 x plus cos x close parentheses cubed equals open parentheses 5 x plus cos x close parentheses to the power of short dash 3 end exponent Rewrite so that the power rule can be used.
f apostrophe open parentheses x close parentheses equals short dash 3 open parentheses 5 x plus cos x close parentheses to the power of short dash 4 end exponent times D open square brackets 5 x plus cos x close square brackets Apply the power rule.
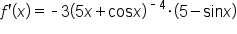
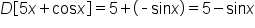
f apostrophe open parentheses x close parentheses equals short dash 3 open parentheses 5 x plus cos x close parentheses to the power of short dash 4 end exponent times open parentheses 5 minus sin x close parentheses D open square brackets 5 x plus cos x close square brackets equals 5 plus open parentheses short dash sin x close parentheses equals 5 minus sin x
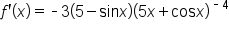
f apostrophe open parentheses x close parentheses equals short dash 3 open parentheses 5 minus sin x close parentheses open parentheses 5 x plus cos x close parentheses to the power of short dash 4 end exponent Rearrange the factors.
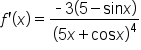
f apostrophe open parentheses x close parentheses equals fraction numerator short dash 3 open parentheses 5 minus sin x close parentheses over denominator open parentheses 5 x plus cos x close parentheses to the power of 4 end fraction Rewrite with nonnegative exponents.

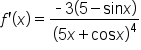Thus, f apostrophe open parentheses x close parentheses equals fraction numerator short dash 3 open parentheses 5 minus sin x close parentheses over denominator open parentheses 5 x plus cos x close parentheses to the power of 4 end fraction.

try it
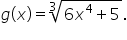
Consider the function g open parentheses x close parentheses equals cube root of 6 x to the power of 4 plus 5 end root.
Find the derivative.
First, rewrite as g open parentheses x close parentheses equals open parentheses 6 x to the power of 4 plus 5 close parentheses to the power of 1 divided by 3 end exponent.

The function is in the form y equals open square brackets f open parentheses x close parentheses close square brackets to the power of 1 divided by 3 end exponent comma where f open parentheses x close parentheses equals 6 x to the power of 4 plus 5.

Then, by the general power rule, g apostrophe open parentheses x close parentheses equals 1 third open square brackets f open parentheses x close parentheses close square brackets to the power of short dash 2 divided by 3 end exponent times f apostrophe open parentheses x close parentheses.

Since f apostrophe open parentheses x close parentheses equals 24 x cubed comma we have g apostrophe open parentheses x close parentheses equals 1 third open parentheses 6 x to the power of 4 plus 5 close parentheses to the power of short dash 2 divided by 3 end exponent times 24 x cubed.

Rearranging factors, this becomes g apostrophe open parentheses x close parentheses equals 1 third open parentheses 24 x cubed close parentheses open parentheses 6 x to the power of 4 plus 5 close parentheses to the power of short dash 2 divided by 3 end exponent comma which simplifies to g apostrophe open parentheses x close parentheses equals 8 x cubed open parentheses 6 x to the power of 4 plus 5 close parentheses to the power of short dash 2 divided by 3 end exponent.

Finally, writing in terms of nonnegative exponents: g apostrophe open parentheses x close parentheses equals fraction numerator 8 x cubed over denominator open parentheses 6 x to the power of 4 plus 5 close parentheses to the power of 2 divided by 3 end exponent end fraction

EXAMPLE

The distance (measured in feet) from a moving camera to an object positioned at the point (1, 4) is given by the function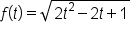 f open parentheses t close parentheses equals square root of 2 t squared minus 2 t plus 1 end root, where t is measured in seconds. At what rate is the distance changing after 3 seconds?

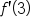Mathematically speaking, we want to compute f apostrophe open parentheses 3 close parentheses.

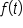To find the derivative, we first need to rewrite f open parentheses t close parentheses:

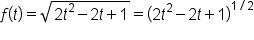
f open parentheses t close parentheses equals square root of 2 t squared minus 2 t plus 1 end root equals open parentheses 2 t squared minus 2 t plus 1 close parentheses to the power of 1 divided by 2 end exponent Write the radical as 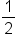1 half power.
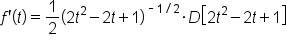
f apostrophe open parentheses t close parentheses equals 1 half open parentheses 2 t squared minus 2 t plus 1 close parentheses to the power of short dash 1 divided by 2 end exponent times D open square brackets 2 t squared minus 2 t plus 1 close square brackets Apply the power rule.
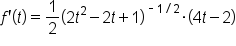
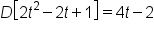
f apostrophe open parentheses t close parentheses equals 1 half open parentheses 2 t squared minus 2 t plus 1 close parentheses to the power of short dash 1 divided by 2 end exponent times open parentheses 4 t minus 2 close parentheses D open square brackets 2 t squared minus 2 t plus 1 close square brackets equals 4 t minus 2
f apostrophe open parentheses t close parentheses equals 1 half open parentheses 4 t minus 2 close parentheses times open parentheses 2 t squared minus 2 t plus 1 close parentheses to the power of short dash 1 divided by 2 end exponent Rearrange the terms.
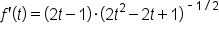
f apostrophe open parentheses t close parentheses equals open parentheses 2 t minus 1 close parentheses times open parentheses 2 t squared minus 2 t plus 1 close parentheses to the power of short dash 1 divided by 2 end exponent Distribute 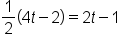1 half open parentheses 4 t minus 2 close parentheses equals 2 t minus 1
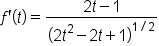
f apostrophe open parentheses t close parentheses equals fraction numerator 2 t minus 1 over denominator open parentheses 2 t squared minus 2 t plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction Rewrite with nonnegative exponents.

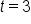Now, we desire the rate of change when t equals 3, so we substitute 3.

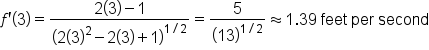
f apostrophe open parentheses 3 close parentheses equals fraction numerator 2 open parentheses 3 close parentheses minus 1 over denominator open parentheses 2 open parentheses 3 close parentheses squared minus 2 open parentheses 3 close parentheses plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction equals 5 over open parentheses 13 close parentheses to the power of 1 divided by 2 end exponent almost equal to 1.39 space feet space per space second

2. Combining Derivative Rules

Now that we are building up our derivative rules, we can find derivatives of more complex functions.

EXAMPLE

Find the derivative of the function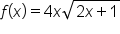 f open parentheses x close parentheses equals 4 x square root of 2 x plus 1 end root.

At this point, we are conditioned to write radicals as fractional powers (to use the power rule).

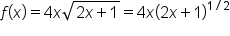
f open parentheses x close parentheses equals 4 x square root of 2 x plus 1 end root equals 4 x open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent Rewrite the square root as 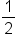1 half power.
f apostrophe open parentheses x close parentheses equals D open square brackets 4 x close square brackets times open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent plus 4 x times D open square brackets open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent close square brackets Apply the product rule.
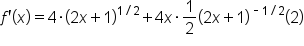
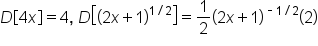
f apostrophe open parentheses x close parentheses equals 4 times open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent plus 4 x times 1 half open parentheses 2 x plus 1 close parentheses to the power of short dash 1 divided by 2 end exponent open parentheses 2 close parentheses D open square brackets 4 x close square brackets equals 4 comma space D open square brackets open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent close square brackets equals 1 half open parentheses 2 x plus 1 close parentheses to the power of short dash 1 divided by 2 end exponent open parentheses 2 close parentheses
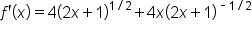
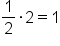f apostrophe open parentheses x close parentheses equals 4 open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent plus 4 x open parentheses 2 x plus 1 close parentheses to the power of short dash 1 divided by 2 end exponent 1 half times 2 equals 1; remove excess symbols.
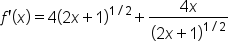
f apostrophe open parentheses x close parentheses equals 4 open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent plus fraction numerator 4 x over denominator open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction Rewrite with positive exponents.

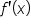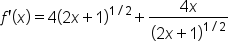At this point, f apostrophe open parentheses x close parentheses is reasonably simplified. Thus, f apostrophe open parentheses x close parentheses equals 4 open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent plus fraction numerator 4 x over denominator open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction.

It is possible to go further by forming a common denominator and combining the fractions. Let’s see how this plays out:

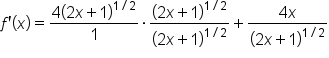
f apostrophe open parentheses x close parentheses equals fraction numerator 4 open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent over denominator 1 end fraction times open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent over open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent plus fraction numerator 4 x over denominator open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction The common denominator is 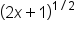open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent.
Write 4 open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent over 1 so it “looks” like a fraction.
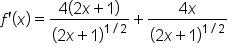
f apostrophe open parentheses x close parentheses equals fraction numerator 4 open parentheses 2 x plus 1 close parentheses over denominator open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction plus fraction numerator 4 x over denominator open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction Perform multiplication.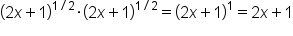
open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent times open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent equals open parentheses 2 x plus 1 close parentheses to the power of 1 equals 2 x plus 1
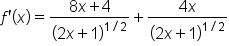
f apostrophe open parentheses x close parentheses equals fraction numerator 8 x plus 4 over denominator open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction plus fraction numerator 4 x over denominator open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction Distribute 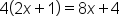4 open parentheses 2 x plus 1 close parentheses equals 8 x plus 4.
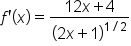
f apostrophe open parentheses x close parentheses equals fraction numerator 12 x plus 4 over denominator open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction Combine the numerators.

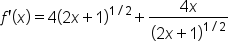As you can see, the expression simplified nicely to one single fraction. That said, writing f apostrophe open parentheses x close parentheses equals 4 open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent plus fraction numerator 4 x over denominator open parentheses 2 x plus 1 close parentheses to the power of 1 divided by 2 end exponent end fraction is equally acceptable.

watch
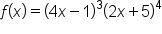Sometimes factoring is very useful in obtaining a nicer form of the derivative. In the following video, we’ll take the derivative of f open parentheses x close parentheses equals open parentheses 4 x minus 1 close parentheses cubed open parentheses 2 x plus 5 close parentheses to the power of 4 and write it in factored form.

try it
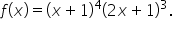
Consider the function f open parentheses x close parentheses equals open parentheses x plus 1 close parentheses to the power of 4 open parentheses 2 x plus 1 close parentheses cubed.
Find the derivative and write your final answer in factored form.
Note that f open parentheses x close parentheses is a product of two functions: open parentheses x plus 1 close parentheses to the power of 4 and open parentheses 2 x plus 1 close parentheses cubed.

Then:

f apostrophe open parentheses x close parentheses equals open parentheses 2 x plus 1 close parentheses cubed times D open square brackets open parentheses x plus 1 close parentheses to the power of 4 close square brackets plus open parentheses x plus 1 close parentheses to the power of 4 times D open square brackets open parentheses 2 x plus 1 close parentheses cubed close square brackets space space space space space space space space equals open parentheses 2 x plus 1 close parentheses cubed times 4 open parentheses x plus 1 close parentheses cubed open parentheses 1 close parentheses plus open parentheses x plus 1 close parentheses to the power of 4 times 3 open parentheses 2 x plus 1 close parentheses squared open parentheses 2 close parentheses space space space space space space space space equals 4 open parentheses 2 x plus 1 close parentheses cubed open parentheses x plus 1 close parentheses cubed plus 6 open parentheses x plus 1 close parentheses to the power of 4 open parentheses 2 x plus 1 close parentheses squared

Now, look at the two large “terms” 4 open parentheses 2 x plus 1 close parentheses cubed open parentheses x plus 1 close parentheses cubed and 6 open parentheses x plus 1 close parentheses to the power of 4 open parentheses 2 x plus 1 close parentheses squared. The terms have a common factor of 2 open parentheses x plus 1 close parentheses cubed open parentheses 2 x plus 1 close parentheses squared comma so we factor this out: 

f apostrophe open parentheses x close parentheses equals 2 open parentheses x plus 1 close parentheses cubed open parentheses 2 x plus 1 close parentheses squared open square brackets 2 open parentheses 2 x plus 1 close parentheses plus 3 open parentheses x plus 1 close parentheses close square brackets

The quantity inside the brackets simplifies as follows:

2 open parentheses 2 x plus 1 close parentheses plus 3 open parentheses x plus 1 close parentheses equals 4 x plus 2 plus 3 x plus 3 equals 7 x plus 5

Thus, the final factored form is f apostrophe open parentheses x close parentheses equals 2 open parentheses x plus 1 close parentheses cubed open parentheses 2 x plus 1 close parentheses squared open parentheses 7 x plus 5 close parentheses.

summary
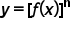In this lesson, you learned how to apply the general power rule for derivatives of functions, such as the form bold italic y bold equals bold left square bracket bold italic f bold left parenthesis bold italic x bold right parenthesis bold right square bracket to the power of bold n. As you develop your repertoire of derivative formulas, you are able to combine derivative rules to find derivatives of more complex functions, such as the ones explored in this unit.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 2 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Formulas to Know
General Power Rule for Derivatives of Functions

If f open parentheses x close parentheses is some function, then D open square brackets open square brackets f open parentheses x close parentheses close square brackets to the power of n close square brackets equals n times open square brackets f open parentheses x close parentheses close square brackets to the power of n minus 1 end exponent times f apostrophe open parentheses x close parentheses.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.