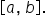 Recall that the average of a set of numbers is the sum of the numbers, divided by the number of numbers. This takes on a different meaning for continuous functions. Specifically, this lesson will cover:
Recall that the average of a set of numbers is the sum of the numbers, divided by the number of numbers. This takes on a different meaning for continuous functions. Specifically, this lesson will cover:
Table of Contents |
When finding the average of a set of numbers, you add up all the numbers, then divide by how many numbers there are.
EXAMPLE
Given the numbers 81, 85, 89, and 71, the average of these four numbers is
Now consider a function  on some interval
on some interval 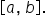 Break up the interval
Break up the interval  into n equal subintervals. Then, select a value of x from each subinterval. Call these values
into n equal subintervals. Then, select a value of x from each subinterval. Call these values 
Then, the average of these values is 
The summation resembles a Riemann sum, but the  term is missing inside the summation. Recall that
term is missing inside the summation. Recall that 
We can multiply the summation by 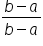 as follows:
as follows:
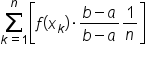
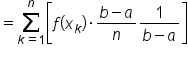
 with
with 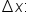

 is a constant, it can be factored out and written in front of the summation:
is a constant, it can be factored out and written in front of the summation:

 approaches the value of
approaches the value of  as
as  as long as
as long as  is integrable on
is integrable on 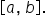 Since we are assuming
Since we are assuming  is continuous on
is continuous on 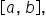
 is also integrable on
is also integrable on 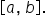
Note that the summation for the average value is the Riemann sum for  but multiplied by
but multiplied by 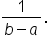
This leads to an integral formula to find the average value of a continuous function  on an interval
on an interval 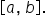
 is continuous on the closed interval
is continuous on the closed interval 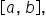 then the average value of
then the average value of  on
on  is
is 
 the average value of a nonnegative function
the average value of a nonnegative function  on
on 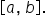 The figure below shows an illustration of this.
The figure below shows an illustration of this.
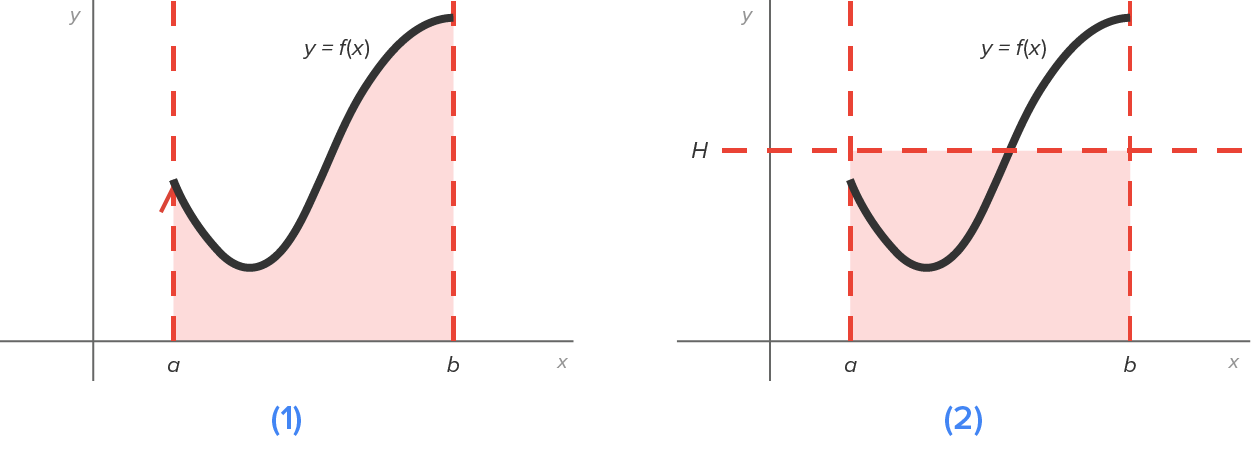
 and the x-axis on
and the x-axis on 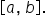
 Note that the base is
Note that the base is  and its height is H, where H is the average value of
and its height is H, where H is the average value of  on
on 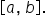
 is equal to the area of the region bounded by the graph of
is equal to the area of the region bounded by the graph of  and the x-axis on
and the x-axis on 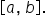
Now that we have a formula for average value, let’s compute and interpret average values.
EXAMPLE
Find the average value of on the interval
on the interval 
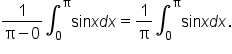
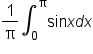
|
Start with the original expression. |
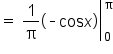
|
Apply the fundamental theorem of calculus. |
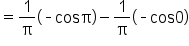
|
Substitute the upper and lower endpoints. |
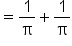
|
Evaluate the parentheses. |
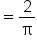
|
Simplify. |
 on the interval
on the interval  is equal to
is equal to 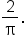
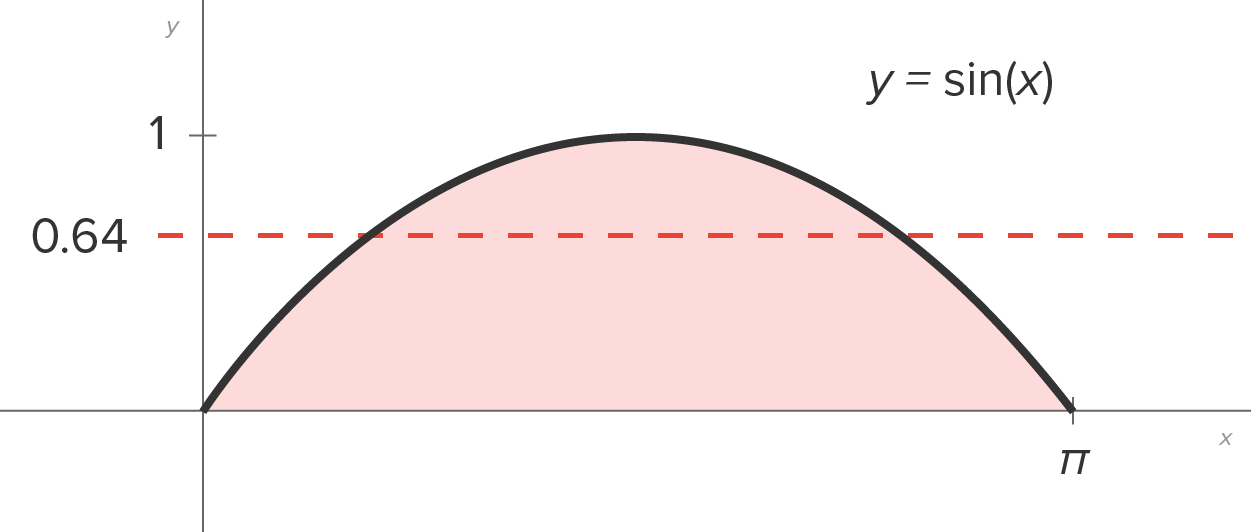
 and the x-axis on the interval
and the x-axis on the interval  and the rectangle whose height is the average value and whose width is
and the rectangle whose height is the average value and whose width is 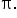 Note:
Note: 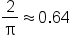
 on the interval
on the interval 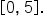

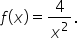
EXAMPLE
During a 9-hour workday, the production rate at time t hours is cars per hour. What is the average hourly production rate?
cars per hour. What is the average hourly production rate?
 over the interval
over the interval 
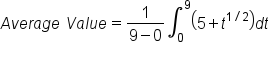
|
Start with the original expression. Rewrite
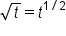 to be able to use the power rule. to be able to use the power rule.
|

|
Apply the fundamental theorem of calculus. |
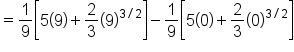
|
Substitute the upper and lower endpoints. |
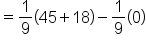
|
Evaluate. |
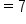
|
Simplify. |
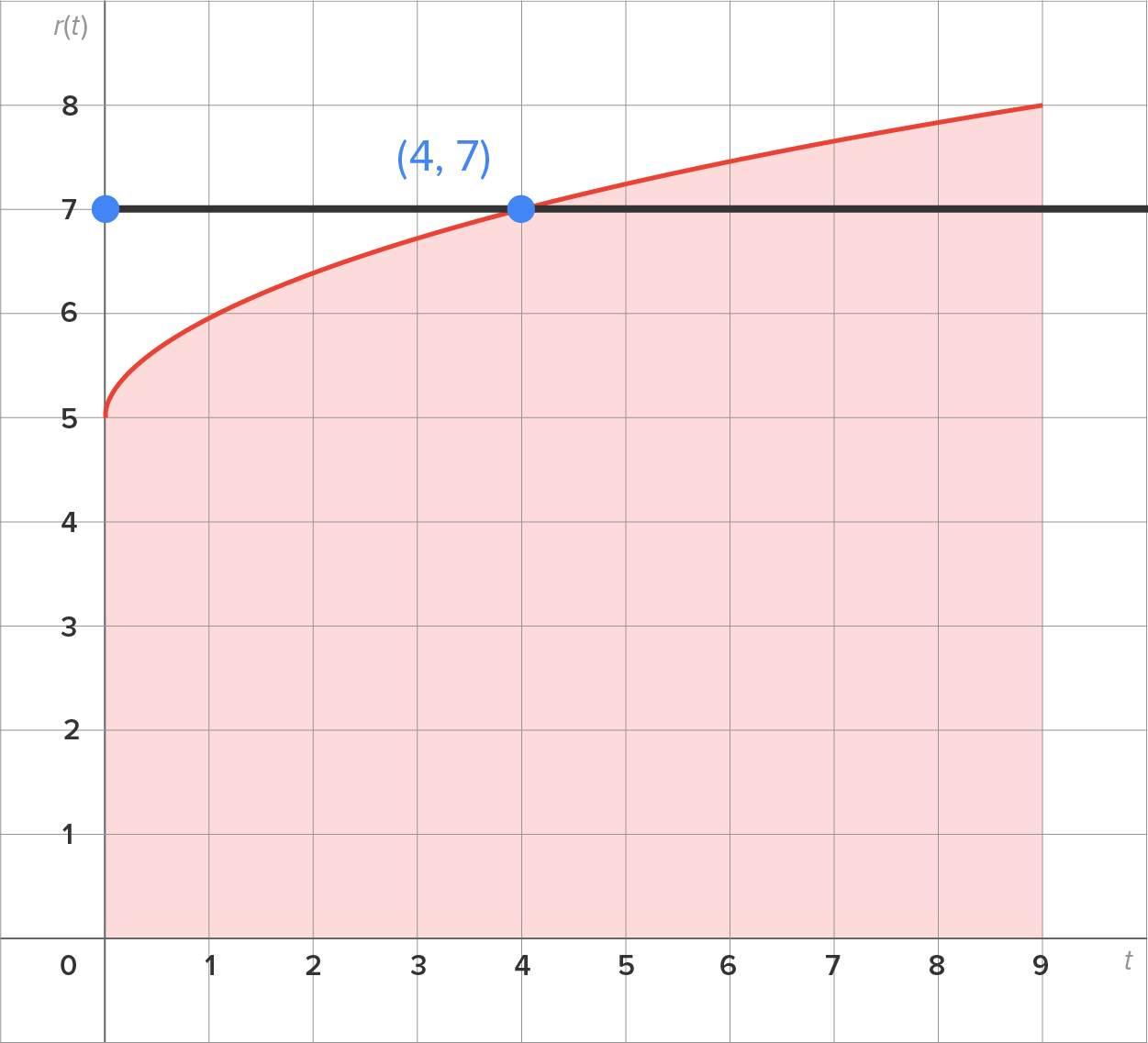
 and the t-axis, as well as the horizontal line
and the t-axis, as well as the horizontal line  Note that the area between
Note that the area between  and the t-axis is equal to the area of the rectangle with the same base (9) and height 7 (the average value).
and the t-axis is equal to the area of the rectangle with the same base (9) and height 7 (the average value).
 on an interval
on an interval 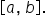 You also learned how the fundamental theorem of calculus can be used to compute the average value of a continuous function
You also learned how the fundamental theorem of calculus can be used to compute the average value of a continuous function  on an interval
on an interval 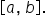
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 4 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.