In this lesson, you will learn how to evaluate a series using summation notation. Specifically, this lesson will cover:
1. Sequences and Series
A sequence is a set of numbers in a particular order. It has elements or terms in curly braces (which define it as a set), and the terms are in numerical order (increasing in value).
-
EXAMPLE
{4, 7, 10, 13, 16} is a sequence.
One application of sequences is to add the terms together. We call this a series.
-
EXAMPLE
To evaluate the series of the sequence {4, 7, 10, 13, 16} we simply add the numbers together. This particular series evaluates to 50.
-
- Sequence
- A set of numbers in a particular order.
- Series
- The sum of the first n terms in a sequence.
2. Summation Notation
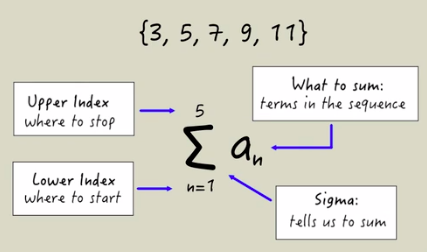
Summation notation is a way to write the sum of sequences. Let's us the sequence {3, 5, 7, 9, 11} to write the series in summation notation:
-
Sigma: This notation tells us to sum the values of terms in a sequence, starting with the first term and ending with the fifth term. How was this information drawn out from this notation? The big E-like symbol is the Greek letter sigma. This is what tells us to sum, or add.
-
What to sum: What exactly are we summing? That's written directly to the right of sigma. The
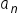 represents the value of the n-th term to a sequence.
represents the value of the n-th term to a sequence.
-
Lower index: Below is the lower index, which tells us where to start summing. In this case, the lower index is 1.
-
Upper index: Above is the upper index, which tells us where to stop summing. In this case, the upper index is 5.
All of this together is telling us to evaluate
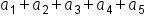
where each of these terms represents the values of the first, second, third, fourth, and fifth terms of a sequence, respectively.
-
- Summation Notation
- An expression of a series, using the Greek letter sigma, and a lower and upper index to indicate the first and last terms of the sum.
3. Evaluating a Series using Summation Notation
Next, let's practice using a defined sequence and summation notation to evaluate a series.
-
EXAMPLE
Consider this example sequence {12, 8, 4, 0, -4, -8, ...}. Notice, however, that this is now an infinite sequence, meaning that more terms follow -8.
How can we interpret what we are asked to sum from the following notation:
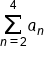
-
Sigma: We should first note what this is asking us to sum due to the sigma symbol. This is telling us to add values of terms in a sequence.
-
What to add: Our sequence is defined as
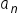 , so this is asking us to add together terms in that particular sequence.
, so this is asking us to add together terms in that particular sequence.
-
Lower index: Next, we should examine the lower index, which tells us what term is the start of our sum, in this case, 2.
-
Upper index: Then, we should examine the upper index as well, which tells us which term will end the sum, in this case, 4.
So this notation tells us to add together the second through fourth terms of the sequence. The second term is 8, the third term is 4, and the fourth term is 0.
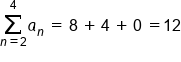
This would be
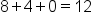
as the value of the series.
When defining sequences and series, we can say that a sequence is a set of numbers in a particular order and a series is the sum of the first n terms in a sequence. Summation notation is an expression of a series from a lower index term up to and including an upper index term. When evaluating a series using summation notation, it is important to note what it is asking us to sum.

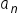 represents the value of the n-th term to a sequence.
represents the value of the n-th term to a sequence. 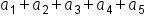 where each of these terms represents the values of the first, second, third, fourth, and fifth terms of a sequence, respectively.
where each of these terms represents the values of the first, second, third, fourth, and fifth terms of a sequence, respectively.
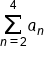
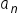 , so this is asking us to add together terms in that particular sequence.
, so this is asking us to add together terms in that particular sequence. 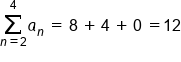
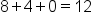 as the value of the series.
as the value of the series.