Table of Contents |
With straight line depreciation, we are assuming that the life of the asset is assumed to be used up as a constant rate over its useful life. Straight line depreciation should be used if there is consistent usage of the asset over the asset's useful life, meaning there are no large fluctuations, increases or decreases, in terms of the usage level of that asset over time.
EXAMPLE
Buildings aren't necessarily used more in the early years and less in the later years of their lifespan. Generally speaking, they are used consistently over their useful life.A major benefit of straight line depreciation is simplicity. The asset is depreciated in equal dollar amounts over the useful life of the asset; therefore, it's going to be the same depreciation amount every year. This significantly simplifies the depreciation calculation that needs to be performed.
The calculation for a straight line depreciation is cost minus residual value, divided by the number of years of the asset's useful life.
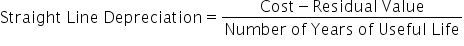
Now, let's break down this calculation further into its component parts:.
The straight line depreciation calculation provides an annual amount. Note, we can also break it down into monthly depreciation by dividing our calculated straight line depreciation amount by 12. In addition, if we're looking for the amount of accumulated depreciation as of a certain month, we would simply multiply that monthly amount by the number of months that we're looking for.
Next, let's take a look at our straight line depreciation formula by performing some calculations with some example scenarios. For each example, we'll need to know:
For the first example, the total cost of the asset is $500,000, and we're going to assume it has a residual value of $15,000 and a useful life of 10 years.
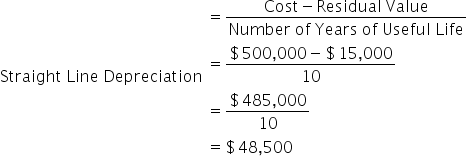
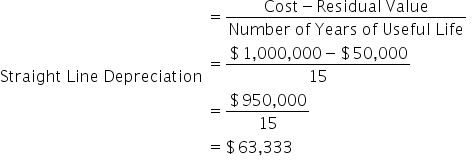
For the next example, we're going to assume we have a total cost of $1,000,000, a residual value of $50,000, and a useful life of 15 years.
Now, we can break that down even further by looking at the monthly depreciation. In this case, every month, depreciation would be $5,278.

If we wanted to see what the accumulated depreciation would be at a certain point in time, we can take that monthly depreciation amount and multiply it by the number of months that we want to find. In this example, after 36 months, the total accumulated depreciation would be $190,008, which is the monthly depreciation multiplied by 36.
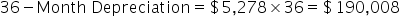
Source: THIS TUTORIAL WAS AUTHORED BY EVAN MCLAUGHLIN FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.