Table of Contents |
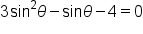 on the interval
on the interval 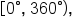 take a look at this video.
take a look at this video.
EXAMPLE
Consider the equation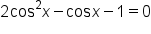 on the interval
on the interval 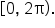
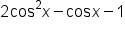 contains a square term and a linear term in cosine, and a constant term.
contains a square term and a linear term in cosine, and a constant term.
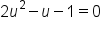
|
Let 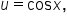 then substitute. then substitute.
|
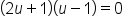
|
Factor. |
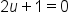 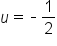
|
Set 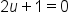 and solve. and solve.
|
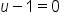 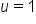
|
Set 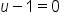 and solve. and solve.
|
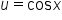 so we can solve the equation for x.
so we can solve the equation for x.

|
Back-substitute 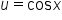 into the equation into the equation 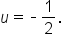
|
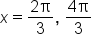
|
Using the unit circle, these are the angles that correspond to 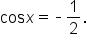
|
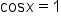
|
Back-substitute 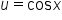 into the equation into the equation 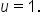
|
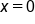
|
From the unit circle, 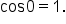
|
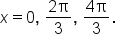
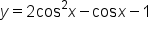 is shown below. Note the locations of the x-intercepts on the interval
is shown below. Note the locations of the x-intercepts on the interval 
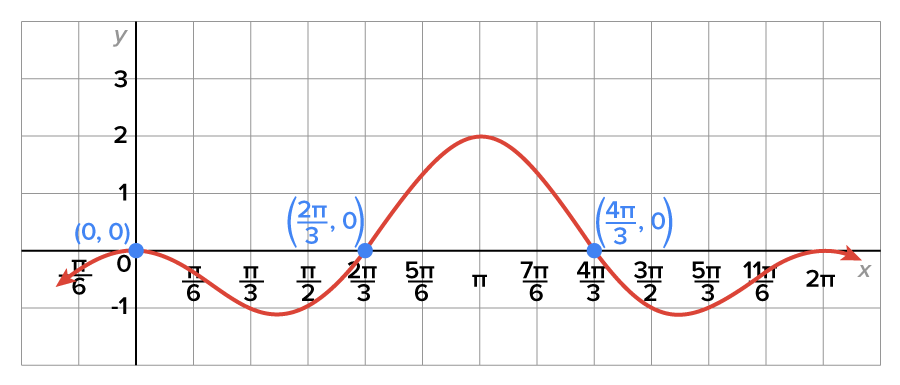
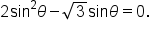
There are instances where the equation can’t be solved easily as written, so an identity is used to rewrite.
EXAMPLE
Consider the equation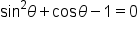 on the interval
on the interval 
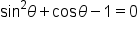
|
This is the original equation. |
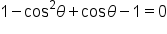
|
Use the Pythagorean identity 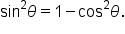
|
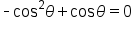
|
Combine like terms. |
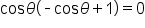
|
Factor out 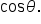
|
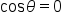
|
Set the first factor equal to 0. |
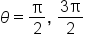
|
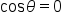 when when 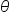 is an odd multiple of is an odd multiple of 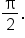
|
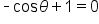
|
Set the second factor equal to 0. |
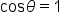
|
Add 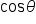 to both sides and write to both sides and write 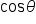 on the left side. on the left side.
|
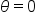
|
From the unit circle, 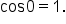
|
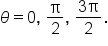
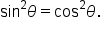
EXAMPLE
Consider the equation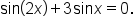
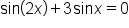
|
This is the original equation. |
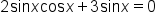
|
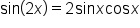
|
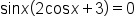
|
Factor. |
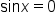
|
Set the first factor equal to 0. |
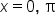
|
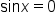 when x is an integer multiple of when x is an integer multiple of 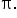
|
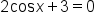
|
Set the second factor equal to 0. |
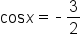
|
Subtract 3 from both sides, then divide by 2. |
| No solution |
Since 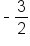 is not in the range of the cosine function, there is no solution to this equation. is not in the range of the cosine function, there is no solution to this equation.
|
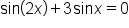 are
are 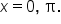
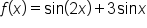 on the interval
on the interval 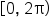 and note that its x-intercepts are
and note that its x-intercepts are 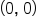 and
and 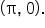
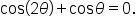
This next example is quite different from the others since the above strategies do not apply. How will we solve it?
EXAMPLE
Consider the equation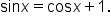 Find all solutions on the interval
Find all solutions on the interval 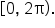
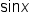 with an expression involving
with an expression involving 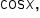 or vice versa.
or vice versa.
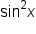 and
and 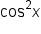 are related through a Pythagorean identity, so it may be worth a try to square both sides of the equation.
are related through a Pythagorean identity, so it may be worth a try to square both sides of the equation.
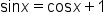
|
This is the original equation. |
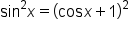
|
Square both sides. |
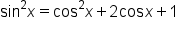
|
Expand the right side. |
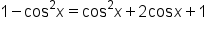
|
Replace 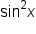 with with 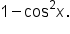
|
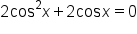
|
Add 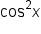 to both sides, and subtract 1 from both sides. Then, write the expression on the left side. to both sides, and subtract 1 from both sides. Then, write the expression on the left side.
|
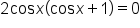
|
Factor out 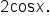
|
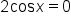
|
Set the first factor equal to 0. |
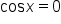
|
Divide both sides by 2. |
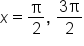
|
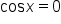 when x is an odd multiple of when x is an odd multiple of 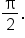
|
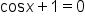
|
Set the second factor equal to 0. |
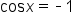
|
Subtract 1 from both sides. |
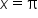
|
This is the solution. |
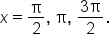
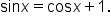
| Potential Solution | Left Side of Equation | Right Side of Equation | Does It Check? |
|---|---|---|---|
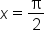
|
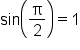
|
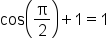
|
Yes |
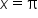
|
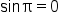
|
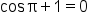
|
Yes |
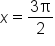
|

|
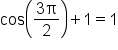
|
No |
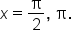
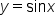 and
and 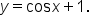 Note the intersection points.
Note the intersection points.
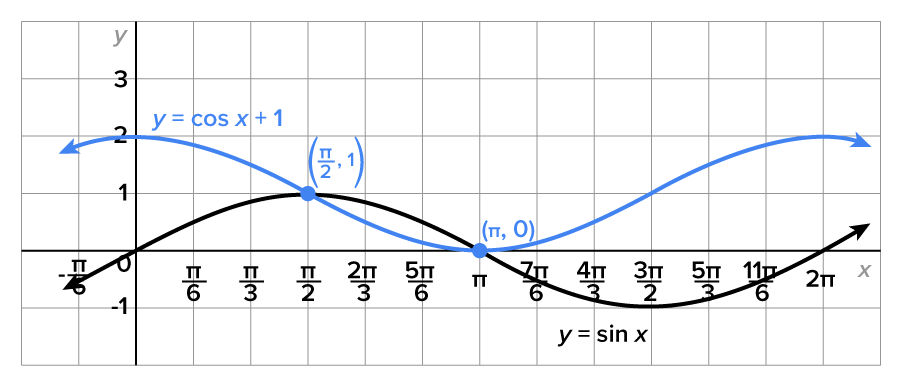
So far, we have solved trigonometric equations where the angle is x. How do things change when the angle is a multiple of x, such as 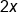 or
or 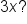
Consider the function 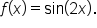 The period of this function is
The period of this function is 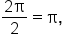 meaning it goes through one full oscillation from
meaning it goes through one full oscillation from 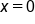 to
to 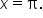 As a result, the graph goes through two full oscillations
As a result, the graph goes through two full oscillations 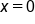 to
to 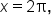 which is the standard interval over which we solve trigonometric equations.
which is the standard interval over which we solve trigonometric equations.
Note that when 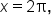 the angle
the angle 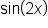 is
is 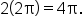 Thus, from
Thus, from 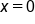 to
to 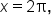 the angle of the expression
the angle of the expression 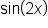 starts at
starts at 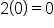 and ends at
and ends at 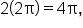 which also represents two full rotations on the unit circle.
which also represents two full rotations on the unit circle.
This is the logic we use to solve trigonometric equations that contain multiple angles that cannot be manipulated through identities.
EXAMPLE
Consider the equation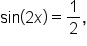 where
where 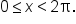
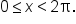
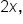 the domain for angle
the domain for angle 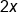 is
is 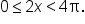
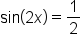 when
when 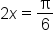 and when
and when 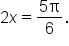
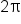 to each angle from the first rotation since they are coterminal:
to each angle from the first rotation since they are coterminal:
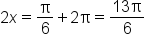 and
and 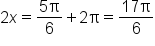
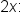
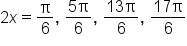
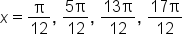
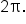
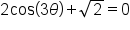 where
where 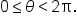
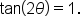
SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS