Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Solving Logarithmic Equations Using Properties of Logarithms

Author: Sophia
PDF Version

what's covered
In this lesson, you will solve logarithmic equations using various properties of logarithms. Specifically, this lesson will cover:

Table of Contents

1. Solving Logarithmic Equations by Converting to Exponential Form

Some logarithmic equations can be solved by writing the equation in its corresponding exponential form.

EXAMPLE

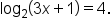
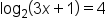
Solve the equation log subscript 2 open parentheses 3 x plus 1 close parentheses equals 4.

log subscript 2 open parentheses 3 x plus 1 close parentheses equals 4 This is the original equation.
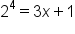
2 to the power of 4 equals 3 x plus 1 Rewrite the logarithmic equation in exponential form.
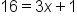
16 equals 3 x plus 1 Simplify.
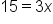15 equals 3 x
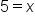
5 equals x 		Solve for x.

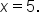The solution is x equals 5. When substituting into the original equation, this checks.

hint
Any solution that causes the argument of a logarithm in the original equation to be negative should be removed as a possible solution.

try it
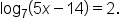
Consider the equation log subscript 7 open parentheses 5 x minus 14 close parentheses equals 2.
Solve the equation for x.
First, rewrite the equation in exponential form, then solve:

log subscript 7 open parentheses 5 x minus 14 close parentheses equals 2 This is the original equation.
7 squared equals 5 x minus 14 Rewrite the logarithm in exponential form.
49 equals 5 x minus 14 Simplify the left-hand side.
63 equals 5 x Add 14 to both sides.
12.6 equals x Divide both sides by 5. This is the solution.

The solution to the equation is x equals 12.6 comma or 63 over 5 in fraction form.

Now let’s look at equations involving natural logarithms.

EXAMPLE

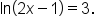
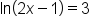
Solve the equation ln   open parentheses 2 x minus 1 close parentheses equals 3.

ln   open parentheses 2 x minus 1 close parentheses equals 3 This is the original equation.
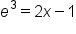
e cubed equals 2 x minus 1 Rewrite the logarithmic equation in exponential form.
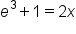e cubed plus 1 equals 2 x
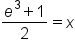
fraction numerator e cubed plus 1 over denominator 2 end fraction equals x 		Solve for x.

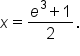The solution is x equals fraction numerator e cubed plus 1 over denominator 2 end fraction. If substituted into the original equation, this checks. The argument is positive when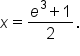 x equals fraction numerator e cubed plus 1 over denominator 2 end fraction.

try it
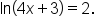
Consider the equation ln   open parentheses 4 x plus 3 close parentheses equals 2.
Solve this equation for x.
Since the logarithm is isolated, convert to exponential form, then solve.

ln   open parentheses 4 x plus 3 close parentheses equals 2 This is the original equation.
e squared equals 4 x plus 3 Recall “ln” corresponds to base e. Convert the equation to exponential form.
e squared minus 3 equals 4 x Subtract 3 from both sides.
fraction numerator e squared minus 3 over denominator 4 end fraction equals x Divide both sides by 4. This is the solution in exact form.

The solution to the equation is x equals fraction numerator e squared minus 3 over denominator 4 end fraction.

2. Solving Logarithmic Equations by Using the One-to-One Property of Logarithms

By the one-to-one property of logarithms, we know that 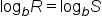log subscript b R equals log subscript b S means that 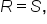R equals S comma provided that R and S are positive.

EXAMPLE

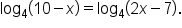
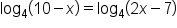
Solve the equation log subscript 4 open parentheses 10 minus x close parentheses equals log subscript 4 open parentheses 2 x minus 7 close parentheses.

log subscript 4 open parentheses 10 minus x close parentheses equals log subscript 4 open parentheses 2 x minus 7 close parentheses This is the original equation.
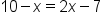
10 minus x equals 2 x minus 7 Apply the one-to-one property.
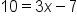10 equals 3 x minus 7
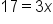17 equals 3 x
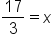
17 over 3 equals x 		Solve for x.

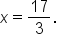The solution is x equals 17 over 3. Substituting into the original equation, this solution checks. The arguments are both positive when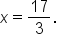 x equals 17 over 3.

try it
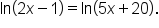
Consider the equation ln   open parentheses 2 x minus 1 close parentheses equals ln   open parentheses 5 x plus 20 close parentheses.
Solve the equation for x.
There is no solution. Solving 2 x minus 1 equals 5 x plus 20 gives x equals short dash 7 comma but substituting x equals short dash 7 into the original equation causes each argument to be negative, making each side undefined.

3. Solving Logarithmic Equations by Using the Product, Quotient, and Power Properties

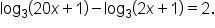Consider the equation log subscript 3 open parentheses 20 x plus 1 close parentheses minus log subscript 3 open parentheses 2 x plus 1 close parentheses equals 2. This equation can’t be solved using the one-to-one property since there is a constant term (+2) in the equation. However, recall that there are properties of logarithms that allow us to write sums, differences, and constant multiples of logarithms as a single logarithm. In our first example, we’ll solve this equation.

EXAMPLE

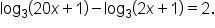
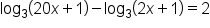
Solve the equation log subscript 3 open parentheses 20 x plus 1 close parentheses minus log subscript 3 open parentheses 2 x plus 1 close parentheses equals 2.

log subscript 3 open parentheses 20 x plus 1 close parentheses minus log subscript 3 open parentheses 2 x plus 1 close parentheses equals 2 This is the original equation.
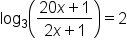
log subscript 3 open parentheses fraction numerator 20 x plus 1 over denominator 2 x plus 1 end fraction close parentheses equals 2 Use the property 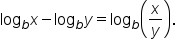log subscript b x minus log subscript b y equals log subscript b open parentheses x over y close parentheses.
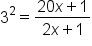
3 squared equals fraction numerator 20 x plus 1 over denominator 2 x plus 1 end fraction Write the logarithm in exponential form.
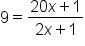
9 equals fraction numerator 20 x plus 1 over denominator 2 x plus 1 end fraction Simplify the left side.
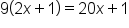
9 open parentheses 2 x plus 1 close parentheses equals 20 x plus 1 Multiply both sides by 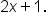2 x plus 1.
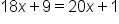
18 x plus 9 equals 20 x plus 1 Distribute.
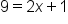9 equals 2 x plus 1
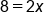8 equals 2 x
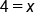
4 equals x 		Solve for x.

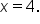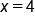The solution is x equals 4. After substituting into the original equation, this checks (both arguments are positive and the equation is satisfied when x equals 4).

Here is an example that involves a different property of logarithms.

EXAMPLE

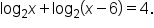
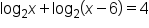
Solve the equation log subscript 2 x plus log subscript 2 open parentheses x minus 6 close parentheses equals 4.

log subscript 2 x plus log subscript 2 open parentheses x minus 6 close parentheses equals 4 This is the original equation.
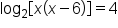
log subscript 2 open square brackets x open parentheses x minus 6 close parentheses close square brackets equals 4 Use the property 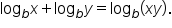log subscript b x plus log subscript b y equals log subscript b open parentheses x y close parentheses.
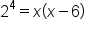
2 to the power of 4 equals x open parentheses x minus 6 close parentheses Rewrite the equation in exponential form.
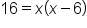
16 equals x open parentheses x minus 6 close parentheses Simplify the left side.
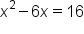
x squared minus 6 x equals 16 Move the variables to the left side.
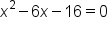
x squared minus 6 x minus 16 equals 0 Subtract 16 from both sides.
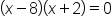open parentheses x minus 8 close parentheses open parentheses x plus 2 close parentheses equals 0
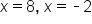
x equals 8 comma space x equals short dash 2 		Factor, then solve.

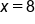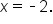It appears there are two solutions, x equals 8 and x equals short dash 2. However, upon checking the original equation, 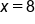x equals 8 checks since both arguments of the logarithms are positive and the equation is satisfied, but 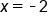x equals short dash 2 causes both arguments of the logarithms to be negative. Therefore, 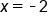x equals short dash 2 is not a solution, and 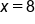x equals 8 is the only solution.

watch
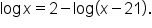Another example is to solve log     x equals 2 minus log   open parentheses x minus 21 close parentheses. Check out the video below to see how it is done.

try it
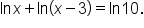
Consider the equation ln     x plus ln   open parentheses x minus 3 close parentheses equals ln   10.
Solve the equation for x.
ln     x plus ln   open parentheses x minus 3 close parentheses equals ln   10 This is the original equation.
ln open square brackets x open parentheses x minus 3 close parentheses close square brackets equals ln   10 Combine logarithms on the left side using the product property.
x open parentheses x minus 3 close parentheses equals 10 Use the one-to-one property.
x squared minus 3 x equals 10 Distribute on the left-hand side.
x squared minus 3 x minus 10 equals 0 The equation is quadratic. Move all terms to one side so that 0 is on one side.
open parentheses x minus 5 close parentheses open parentheses x plus 2 close parentheses equals 0 Factor.
x equals 5 comma space short dash 2 Set each factor equal to 0 and solve. These are the potential solutions.

Since the original equation contains logarithmic terms, it’s important to check each potential solution.

Checking x equals 5 comma we have ln   5 plus ln open parentheses 5 minus 3 close parentheses equals ln   10 comma or ln   5 plus ln   2 equals ln   10 comma which is true.

Checking x equals short dash 2 comma we have ln open parentheses short dash 2 close parentheses plus ln open parentheses short dash 2 minus 3 close parentheses equals ln   10 comma which is not true since ln open parentheses short dash 2 close parentheses is undefined (so is the other logarithmic term).

Therefore, the only solution is x equals 5.

Here is one last example where the power property is required.

EXAMPLE

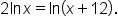
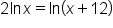
Solve the equation 2   ln     x equals ln   open parentheses x plus 12 close parentheses.

2   ln     x equals ln   open parentheses x plus 12 close parentheses This is the original equation.
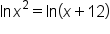
ln     x squared equals ln   open parentheses x plus 12 close parentheses Use the property 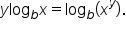y log subscript b x equals log subscript b open parentheses x to the power of y close parentheses.
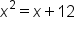
x squared equals x plus 12 Apply the one-to-one property of logarithms.
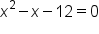x squared minus x minus 12 equals 0
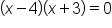open parentheses x minus 4 close parentheses open parentheses x plus 3 close parentheses equals 0
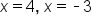
x equals 4 comma space x equals short dash 3 		Solve the quadratic equation for x.

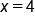Checking each solution in the original equation, x equals 4 checks, but 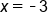x equals short dash 3 does not since the argument of the logarithm is negative. Thus, the solution to this equation is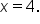 x equals 4.

summary
In this lesson, you learned how to solve logarithmic equations by converting the equation to exponential form, by using the one-to-one property of logarithms, and by applying the product, quotient, and constant multiple properties. It is important to remember to check all possible solutions in the original equation. Any solution that does not make the equation true or causes the argument of a logarithm in the original equation to be negative should be removed as a possible solution.

SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.