Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Solving Logarithmic Equations using Exponents

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to solve a logarithmic equation by rewriting it into an exponential equation. You will also discover how this content strengthens your problem solving skill. Specifically, this lesson will cover:

Table of Contents

1. Rewriting Logarithmic Equations as Exponential Equations

As a review, exponential equations can be equivalently written using a logarithm. In general, we can say that the follow two equations are equivalent:

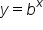
y equals b to the power of x Exponential equation
log subscript b open parentheses y close parentheses equals x Logarithmic equation

For some logarithmic equations, it may be helpful to rewrite the equation as an equivalent exponential equation to solve.

EXAMPLE

Solve the logarithmic equation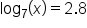 log subscript 7 open parentheses x close parentheses equals 2.8 for x.

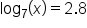
log subscript 7 open parentheses x close parentheses equals 2.8 The logarithmic equation.
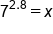
7 to the power of 2.8 end exponent equals x Rewrite into an exponential equation.
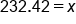
232.42 equals x Use a calculator to evaluate.

big idea
One strategy in solving logarithmic equations is to rewrite it as an exponential equation. In many cases, by doing so, the equation will have an exponential expression on one side of the equation, and an isolated variable on the other side. We can then evaluate the exponential expression to find the solution to the equation.

EXAMPLE

Solve the logarithmic equation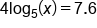 4 log subscript 5 open parentheses x close parentheses equals 7.6 for x.

Notice there is a scalar multiple, 4, in front of the log function.

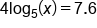
4 log subscript 5 open parentheses x close parentheses equals 7.6 The logarithmic equation.
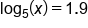
log subscript 5 open parentheses x close parentheses equals 1.9 Divide by 4 to have only 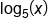log subscript 5 open parentheses x close parentheses on the left side.
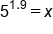
5 to the power of 1.9 end exponent equals x Rewrite into an exponential equation.
21.28 Use a calculator to evaluate.

hint
It is important to have the log expression by itself on one side. In the example above, we had to divide both sides by 4 before we could convert from a logarithmic equation to exponential equation.

2. Logarithm-Exponent Inverse Property

There is one more property of logarithms to explore that will help us solve logarithmic equations. Again, logarithms and exponents are inverse operations of each other. If the 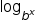log subscript b to the power of x end subscript is an exponent with b as the base, the base and the log function will cancel.

formula to know
Other Properties of Logs
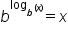
b to the power of log subscript b to the power of open parentheses x close parentheses end exponent end subscript end exponent equals x

An exponential equation involves a constant raised to an exponent that is a variable. If the base number is raised to the log function with the same base, the exponent and log functions will cancel out.

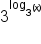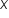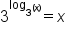Let’s look at the case 3 to the power of log subscript 3 to the power of open parentheses x close parentheses end exponent end subscript end exponent. The constant 3 is raised to an exponent of the log function with the base 3. These functions cancel and we are left with the argument of the log or what is in the parentheses of the log function x. So, 3 to the power of log subscript 3 to the power of open parentheses x close parentheses end exponent end subscript end exponent equals x.

EXAMPLE

Simplify 2 to the power of log subscript 2 to the power of open parentheses y z close parentheses end exponent end subscript end exponent.

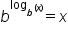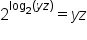Using the inverse property, b to the power of log subscript b to the power of open parentheses x close parentheses end exponent end subscript end exponent equals x, the base 2 is raised to the log function of base 2, so the base and log functions cancel. This will simplify to the argument of the log, yz. So, 2 to the power of log subscript 2 open parentheses y z close parentheses end exponent equals y z.

3. Using the Log Expression as an Exponent

Another method to solve log equations involves applying the inverse relationship between exponents and logs in a slightly different way than you may be used to. We can use the base of the logarithm as a base to an exponent, and place the logarithmic expression as an exponent in the equation. We'll have to do this on both sides of the equation.

EXAMPLE

Solve the logarithmic equation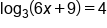 log subscript 3 open parentheses 6 x plus 9 close parentheses equals 4 for x.

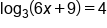The equation has log subscript 3 open parentheses 6 x plus 9 close parentheses equals 4. While we can solve this equation by using the log-exponential relationship, another method is to raise both sides of the equation to the same constant. What helps to simplify the equation is to use the base of the log function as the constant.

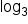So, if we have log subscript 3, raising both sides of the equation as an exponent of the constant 3 will cancel out the log function.

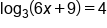
log subscript 3 open parentheses 6 x plus 9 close parentheses equals 4 The logarithmic equation.
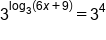
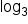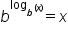3 to the power of log subscript 3 open parentheses 6 x plus 9 close parentheses end exponent equals 3 to the power of 4 Use 3 as a base to cancel out the log subscript 3 function, b to the power of log subscript b to the power of open parentheses x close parentheses end exponent end subscript end exponent equals x.
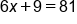
6 x plus 9 equals 81 The left side simplifies to just 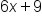6 x plus 9. On the right side, 3 to the 4th power simplifies to 81.
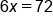
6 x equals 72 Subtract 9 from both sides of the equation.
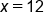
x equals 12 Divide both sides by 6.

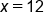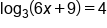So, x equals 12 is the solution of log subscript 3 open parentheses 6 x plus 9 close parentheses equals 4.

big idea
This is essentially a more explicit explanation of the relationship between logarithmic equations and exponential equations. We can use the base of the log to create an exponential equation with the same base. Since logarithms and exponents are inverse operations, this undoes any log or exponent operation, leaving only the argument of the log on one side of the equation, and an exponential expression on the other.

Problem Solving: Why Employers Care
No matter what field you enter, employers are looking for people who are able to understand relationships between concepts and solve problems in creative and effective ways. Understanding that there are multiple paths to solving problems like this helps develop your problem solving skills for other challenges you will face.

summary
In this lesson, you learned that for some logarithmic equations, it may be helpful to rewrite the logarithmic equation as an exponential equation to solve. By doing this, the equation will have an exponential expression on one side of the equation, and an isolated variable on the other side, and you can then evaluate the exponential expression to find the solution to the equation. You also learned that you can use the logarithm-exponent inverse property to solve logarithmic equations; logarithms and exponents are inverse operations of each other, and if the base number is raised to the log function with the same base, the exponent and log functions will cancel out. Lastly, you learned that you can solve logarithmic equations by using the log expression as a exponent to cancel out the logarithm operation, then solving the resulting equation.

Best of luck in your learning!

Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.

Formulas to Know
Other Properties of Logs

b to the power of log subscript b to the power of open parentheses x close parentheses end exponent end subscript end exponent equals x

© 2026 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.