Table of Contents |
When the bases can’t be equated, logarithms are required. Through the one-to-one property of logarithms, we know that for positive quantities R and S, if 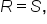 then
then 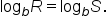
EXAMPLE
Solve the equation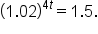

|
This is the original equation. |
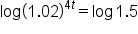
|
Apply the common logarithm to both sides. |
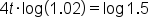
|
Use the power property of logarithms, 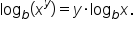
|
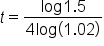
|
Divide both sides by 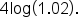
|
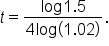 Rounded to three decimal places,
Rounded to three decimal places, 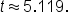
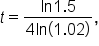 which has the same exact value as
which has the same exact value as 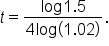
In general, here is the sequence of steps that are required to solve an exponential equation by using logarithms.
EXAMPLE
Solve the equation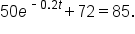
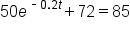
|
This is the original equation. |
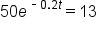
|
Isolate the exponential term on one side. Subtract 72 from both sides. |
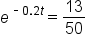 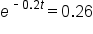
|
Divide both sides by 50. Since 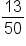 is a terminating decimal, writing it in decimal form doesn’t cause a loss in accuracy. is a terminating decimal, writing it in decimal form doesn’t cause a loss in accuracy.
|
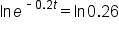
|
Apply the natural logarithm to both sides. |
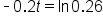
|
Use the inverse property 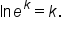
|
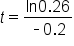
|
Divide both sides by -0.2. |
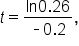 which can also be written
which can also be written 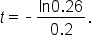 Rounded to three decimal places,
Rounded to three decimal places, 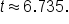
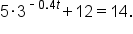
Let’s look at an example with a more complicated exponent.
EXAMPLE
Consider the equation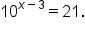
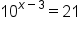
|
This is the original equation. |
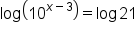
|
Apply the common logarithm to both sides. |
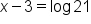
|
Use the inverse property 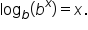
|
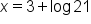
|
Add 3 to both sides. |
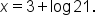 This could also be written as
This could also be written as 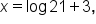 but this could look ambiguous, and one might mistakenly say this is the same as
but this could look ambiguous, and one might mistakenly say this is the same as 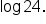
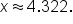
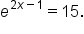
Let’s also explore an exponential equation whose base is neither 10 nor e.
EXAMPLE
Consider the equation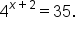
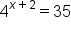
|
This is the original equation. |
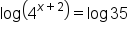
|
Apply the common logarithm to both sides. Note: each side is positive; therefore, both logarithms are defined. |
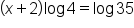
|
Use the power property of logarithms, 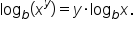
|
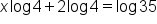
|
Distribute 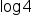 on the left side. on the left side.
|
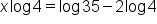
|
Subtract 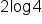 from both sides. from both sides.
|

|
Divide both sides by 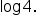
|
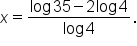 When approximated to three decimal places,
When approximated to three decimal places, 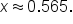
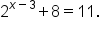
First, let’s look at exponential functions that are set equal to each other.
EXAMPLE
Solve the equation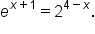
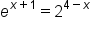
|
This is the original equation. |
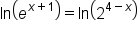
|
Apply the natural logarithm on both sides. |
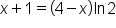
|
On the left side, use the inverse property 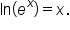 On the right side, use the power property 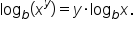
|
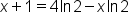
|
Distribute on the right side. |

|
Collect all terms with x on one side of the equation. |
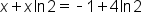
|
Subtract 1 from both sides. |
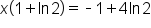
|
Factor out x on the left side. |
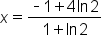
|
Divide both sides by 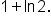
|
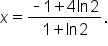 Rounded to three decimal places,
Rounded to three decimal places, 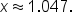
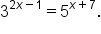
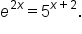
We can also solve exponential functions that are quadratic in form.
EXAMPLE
Solve the equation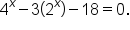

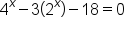
|
This is the original equation. |
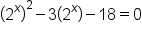
|
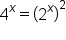
|
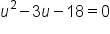
|
Let 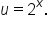
|
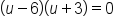 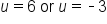
|
Solve the equation for u. |
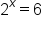
|
Replace u with 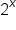 in the equation in the equation 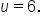
|
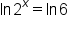
|
Apply the natural logarithm to both sides. |
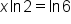
|
Use the property 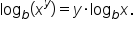
|
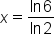
|
Divide both sides by 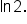
|
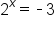
|
Replace u with 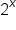 in the equation in the equation 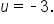
|
| No solution | An exponential function can never be equal to a negative number; therefore, this equation has no solution. |
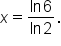 Substituting this value into the original equation verifies that it is a solution.
Substituting this value into the original equation verifies that it is a solution.
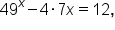 view the following video.
view the following video.
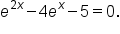
SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS