Table of Contents |
By the one-to-one property of exponential functions, an equation of the form 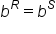 can be solved by setting
can be solved by setting 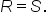
EXAMPLE
Solve the equation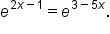
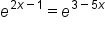
|
This is the original equation. |
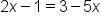
|
Apply the one-to-one property. |
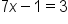 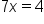 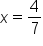
|
Solve for x. |
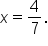
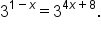
Sometimes the bases are not equal, but it is possible for the exponential functions to be written so that they have the same base.
EXAMPLE
Solve the equation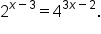
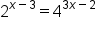
|
This is the original equation. |
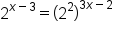
|
Rewrite 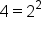 so that the bases on both sides are equal. so that the bases on both sides are equal.
|
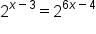
|
Apply the property 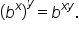
|
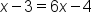
|
Use the one-to-one property. |
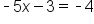 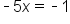 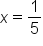
|
Solve for x. |
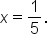 When substituting into the original equation, it checks.
When substituting into the original equation, it checks.
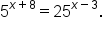
There are even times when it is difficult to write one base as the power of the other, but both bases can be converted to the same base.
EXAMPLE
Solve the equation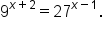
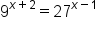
|
This is the original equation. |
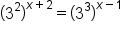
|
Rewrite 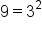 and and 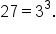
|
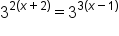
|
Apply the property 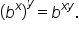
|
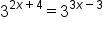
|
Simplify both exponents. |
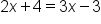
|
Apply the one-to-one property. |
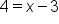 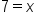
|
Solve for x. |
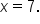 When substituting into the original equation, it checks.
When substituting into the original equation, it checks.
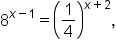 check out the video below.
check out the video below.

SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.