Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Solve Linear Inequalities

Author: Sophia
PDF Version

what's covered
In this lesson, you will define operations of linear inequalities. You will also discover how to solve linear inequalities, similar to solving linear equations. You will also examine how solving these equations strengthens your problem solving skill. Specifically, this lesson will cover:

Table of Contents

1. Operations in Inequality Statements

Just like with equations, you can add or subtract a value on both sides of an inequality and keep the inequality statement true. Just remember that whatever you do to one side of the inequality, you must do to the other side.

EXAMPLE

If you have the inequality 3 is less than 5, and you add 2 to both sides, you have 3 plus 2 is less than 5 plus 2. This simplifies to 5 is less than 7, which is still a true statement.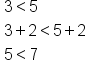

table attributes columnalign left end attributes row cell 3 less than 5 end cell row cell 3 plus 2 less than 5 plus 2 end cell row cell 5 less than 7 end cell end table

You can also multiply or divide by a positive number on both sides and keep the inequality statement true.

EXAMPLE

If you have the inequality 6 is greater than or equal to 4, and you multiply by 3 on both sides, you have 3 times 6 is greater than or equal to 3 times 4. This simplifies to 18 is greater than or equal to 12, which is still true.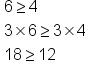

table attributes columnalign left end attributes row cell 6 greater or equal than 4 end cell row cell 3 cross times 6 greater or equal than 3 cross times 4 end cell row cell 18 greater or equal than 12 end cell end table

However, it is important to note that if you multiply or divide by a negative number on both sides of the inequality, the statement becomes untrue until you flip or reverse the inequality sign.

EXAMPLE

If you have the inequality 6 is greater than or equal to 4, and you multiply by a negative 3 on both sides, you have negative 3 times 6 is greater than or equal to negative 3 times 4, which simplifies to negative 18 is greater than or equal to negative 12. This statement is an untrue statement.

table attributes columnalign left end attributes row cell 6 greater or equal than 4 end cell row cell short dash 3 cross times 6 greater or equal than short dash 3 cross times 4 end cell row cell short dash 18 greater or equal than short dash 12 space U N T R U E end cell end table

To correct this statement, we need to flip the sign of the inequality symbol. Instead of the greater than or equal to sign, we would write the less than or equal to sign. When you flip the sign, you now have negative 18 is less than or equal to negative 12, which is a true statement.

table attributes columnalign left end attributes row cell 6 greater or equal than 4 end cell row cell short dash 3 cross times 6 greater or equal than short dash 3 cross times 4 end cell row cell short dash 18 less or equal than short dash 12 space T R U E end cell end table

try it
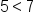Consider the inequality 5 less than 7.
Multiply both sides of the inequality by -2.
5 less than 7 The inequality.
open parentheses short dash 2 close parentheses 5 less than open parentheses short dash 2 close parentheses 7 We multiply both sides of the inequality by -2.
short dash 10 greater than short dash 14 When multiplying or dividing an inequality by a negative number, we must flip the direction of the inequality.

2. Solving Linear Inequalities

You may recall that in solving an equation, you isolate the variable using inverse operations. To isolate the variable, inverse operations are used to get all terms involving the variable on one side of the equation and all other terms to the other side of the equation.

The process for solving an inequality follows the same rules. You use inverse operations to isolate the variable, and what is done on one side of the inequality must be done on the other. The only exception in solving an inequality is that when you multiply or divide both sides of the inequality by a negative number, you must flip the sign of the inequality.

EXAMPLE

Solve 2 x minus 5 less than 1.

2 x minus 5 less than 1 The inequality.
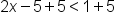
2 x minus 5 plus 5 less than 1 plus 5 Remember to treat the inequality like an equation for now. Isolate the variable by first addressing the constant. Add 5 to both sides.
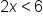
2 x less than 6 The variable is now isolated on the left side.
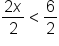
fraction numerator 2 x over denominator 2 end fraction less than 6 over 2 Divide both sides by 2. Because we are dividing by a positive number, we don’t reverse the inequality symbol.
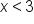
x less than 3 Because we are dividing by a positive number, we don’t reverse the inequality symbol.

hint
Remember, the important difference in solving an inequality is that when you multiply or divide by a negative number, you have to flip the inequality sign.

EXAMPLE

Solve short dash 3 x greater or equal than 12.

short dash 3 x greater or equal than 12 The inequality.
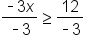
fraction numerator short dash 3 x over denominator short dash 3 end fraction greater or equal than fraction numerator 12 over denominator short dash 3 end fraction Divide both sides by -3.
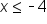
x less or equal than short dash 4 Since we divided by a negative, we need to flip the symbol!

EXAMPLE

Solve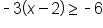 short dash 3 open parentheses x minus 2 close parentheses greater or equal than short dash 6.

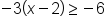
negative 3 left parenthesis x minus 2 right parenthesis greater or equal than negative 6 The inequality.
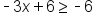
short dash 3 x plus 6 greater or equal than short dash 6 Remember to treat the inequality like an equation for now. Start the process of isolating the variable by using distribution first. Multiply -3 into x and -2 using the distributive property.
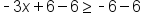
short dash 3 x plus 6 minus 6 greater or equal than short dash 6 minus 6 Isolate the variable by removing the constant on the left side and subtracting 6 from both sides.
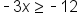
short dash 3 x greater or equal than short dash 12 The constant on the left side is canceled.
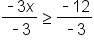
fraction numerator short dash 3 x over denominator short dash 3 end fraction greater or equal than fraction numerator short dash 12 over denominator short dash 3 end fraction Divide both sides by -3.
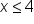
x less or equal than 4 Remember to flip your inequality sign because you are dividing by a negative value.

big idea
The inequality we solve can get as complex as the linear equations we solved. We will use all the same patterns to solve these inequalities as we did for solving equations. Just remember that any time we multiply or divide by a negative, the symbol switches directions (multiplying or dividing by a positive does not change the symbol!)

EXAMPLE

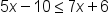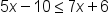
Solve 5 x minus 10 less or equal than 7 x plus 6.

5 x minus 10 less or equal than 7 x plus 6 The inequality.
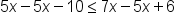
5 x minus 5 x minus 10 less or equal than 7 x minus 5 x plus 6 Subtract 5x from both sides of the inequality.
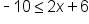
short dash 10 less or equal than 2 x plus 6 The variable is canceled from the left side.
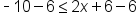
short dash 10 minus 6 less or equal than 2 x plus 6 minus 6 Subtract 6 from both sides.
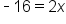
short dash 16 equals 2 x The variable is isolated on the right side.
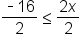
fraction numerator short dash 16 over denominator 2 end fraction less or equal than fraction numerator 2 x over denominator 2 end fraction Divide both sides by 2
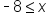
short dash 8 less or equal than x Notice we did not divide by a negative number so the inequality symbol stays the same.

hint
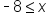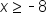Notice that short dash 8 less or equal than x and x greater or equal than short dash 8 are the same intervals. The large open side of the inequality symbol is facing toward the x in both equations, indicating that the x is larger than the -8. In the first interval the x is on the right side of the inequality and in the second, the x variable is on the left side of the interval. It is often easier to understand the interval when the x variable is on the left side of the inequality.

try it
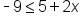Consider the inequality short dash 9 less or equal than 5 plus 2 x.
Solve this inequality.
short dash 9 less or equal than 5 plus 2 x The inequality
short dash 9 minus 5 less or equal than 5 plus 2 x minus 5 Isolate the variable by first addressing the constant. Subtract 5 from both sides.
short dash 14 less or equal than 2 x The constant on the right side is canceled.
fraction numerator short dash 14 over denominator 2 end fraction less or equal than fraction numerator 2 x over denominator 2 end fraction Divide both sides by 2. Because we are dividing by a positive number, 2, we don’t change the inequality symbol.
short dash 7 less or equal than x Because we are dividing by a positive number, 2, we don’t change the inequality symbol. This solution could also be written as x greater or equal than short dash 7 if you preferred to have x be shown first.

try it
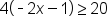Consider the inequality 4 open parentheses short dash 2 x minus 1 close parentheses greater or equal than 20.
Solve this inequality.
4 open parentheses short dash 2 x minus 1 close parentheses greater or equal than 20 The inequality
short dash 8 x minus 4 greater or equal than 20 Start the process of isolating the variable by using distribution first. Multiply 4 into -2x and -1 using the distributive property.
short dash 8 x minus 4 plus 4 greater or equal than 20 plus 4 Isolate the variable by adding 4 to both sides of the inequality.
short dash 8 x greater or equal than 24 The constant on the left side is canceled.
fraction numerator short dash 8 x over denominator short dash 8 end fraction less or equal than fraction numerator 24 over denominator short dash 8 end fraction Divide both sides by -8.
x less or equal than short dash 3 Remember to change your inequality sign because you are dividing by a negative value.

Problem Solving: Solving Linear Inequalities
Working on solving linear inequalities requires you to think analytically, analyze complex problems, and be resilient in working toward a correct answer. These abilities strengthen your problem solving skills, which you can apply in your professional and personal life. While linear inequalities may seem difficult at first, you can persevere in the learning process, proving that you will be able to persevere when approaching other complex and difficult problems.

summary
Today you learned that an inequality is a mathematical statement to show that one quantity is greater than or less than another quantity. You examined the different inequality symbols, including less than, less than or equal to, greater than, and greater than or equal to. You learned about operations in inequality statements, noting that when solving an inequality, you follow the same steps as when solving an equation to isolate the variable; just like with equations, you can add or subtract a value on both sides of an inequality, or multiply or divide by a positive number on both sides, and keep the inequality statement true. However, you also learned that when solving a linear inequality, it is important to remember that the inequality symbol must be flipped when you multiply or divide by a negative number, in order to maintain a true statement. You also reflected on how linear inequality equations strengthen your ability to solve problems in everyday life.

Best of luck in your learning!

Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.