Table of Contents |
Let’s first look at a union of inequalities. This will be the case when you have more than one highlighted range on your number line. For a union of inequalities, we want a true statement from either one inequality OR the other inequality OR both. We can sometimes call these “or” inequalities. This will be similar to interval notation when there is more than one highlighted range; we use the ∪ (union) symbol between two sets of interval notation. For example, 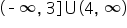 . Again, this means that x can either be in the range
. Again, this means that x can either be in the range 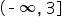 OR can be in the range
OR can be in the range 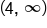 .
.
EXAMPLE
Solve each inequality for x. Write the solution in set notation, interval notation, and graph the solution.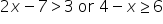
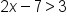
|
The inequality |
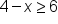
|
The inequality | |
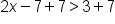
|
Add 7 to both sides of the inequality. |
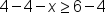
|
Subtract 4 from both sides of the inequality. | |
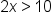
|
Isolate the variable by addressing the coefficient attached to the variable. |
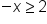
|
Isolate the variable by addressing the coefficient attached to the variable. | |
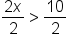
|
Divide both sides by 2. |
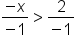
|
Divide both sides by -1. | |
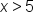
|
x is greater than 5. |
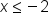
|
Flip the sign of the inequality. x is less than or equal to -2. |
| Compound Inequality | |
|---|---|
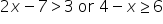
| |
| Solutions | |
|
Set notation: {x | x ≤ -2 or x > 5} |
Interval notation: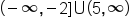
|
| Graph on the number line | |

| |
EXAMPLE
Solve each inequality for x. Write the solution in set notation, interval notation, and graph the solution.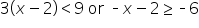
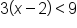
|
The inequality |
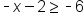
|
The inequality | |
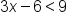
|
Use the distributive property. |
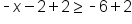
|
Add 2 to both sides of the inequality. | |
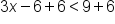
|
Add 6 to both sides of the equation. |
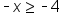
|
Isolate the variable by addressing the coefficient attached to the variable. | |
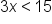
|
Isolate the variable by addressing the coefficient attached to the variable. |
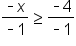
|
Divide both sides of the equation by -1. Remember to flip the inequality symbol. | |
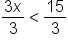
|
Divide both sides of the inequality by 3. |
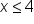
|
x is less than or equal to 4. | |
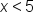
|
x is less than 5. |
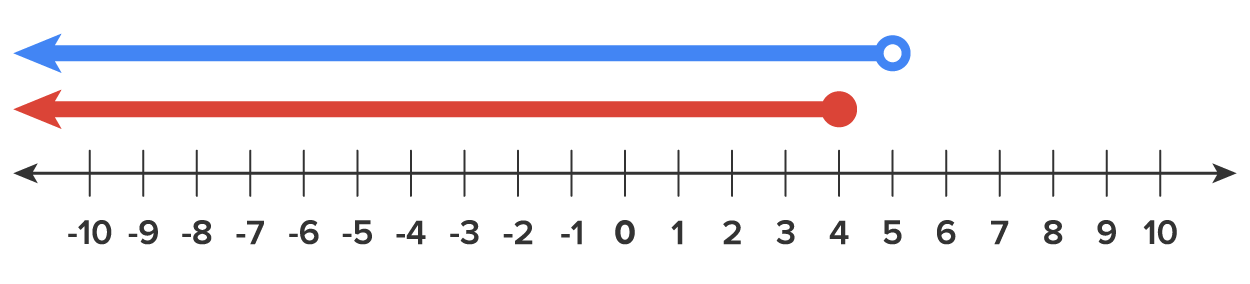
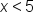 . Here we would only have one solution,
. Here we would only have one solution, 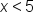 .
.
| Compound Inequality | |
|---|---|
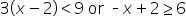
| |
| Solutions | |
|
Set notation: {x | x < 5} |
Interval notation: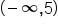
|
| Graph on the number line | |

| |
The second type of compound inequality is the intersection of inequalities. The solution of this type of inequality is only where two or more inequalities overlap. When our solution is given in interval notation, it will be expressed in a manner very similar to single inequalities.
EXAMPLE
Solve each inequality for x. Write the solution in interval notation and graph the solution.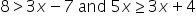
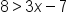
|
The inequality |
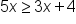
|
The inequality | |
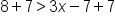
|
Add 7 to both sides of the inequality. |
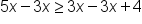
|
Subtract 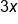 from both sides of the inequality. from both sides of the inequality.
|
|
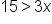
|
Isolate the variable by addressing the coefficient attached to the variable. |
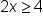
|
Isolate the variable by addressing the coefficient attached to the variable. | |
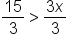
|
Divide both sides of the inequality by 3. |
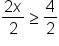
|
Divide both sides of the inequality by 2. | |
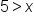
|
x is less than 5. |
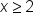
|
x is greater than or equal to 2. |
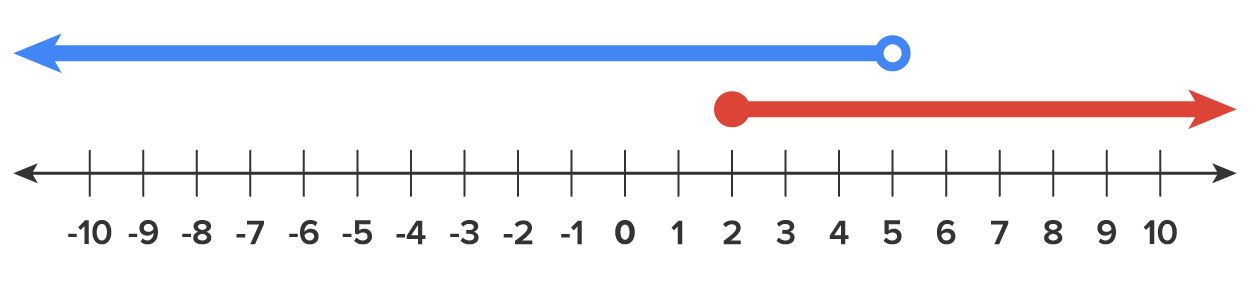
| Compound Inequality | |
|---|---|
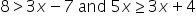
| |
| Solutions | |
|
Set notation: {x | x < 5 and x ≥ 2} |
Interval notation: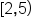
|
| Graph on the number line | |

| |
EXAMPLE
Solve each inequality for x. Write the solution in interval notation.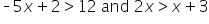
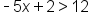
|
The inequality |
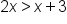
|
The inequality | |
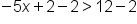
|
Subtract 2 from both sides of the inequality. |
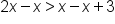
|
Subtract x from both sides of the inequality. | |
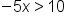
|
Isolate the variable by addressing the coefficient attached to the variable. |
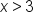
|
x is greater than 3. | |
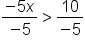
|
Divide both sides by -5 and flip the inequality sign. | |||
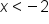
|
x is less than -2. |
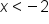 and
and 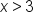 . Let’s graph these intervals on the number line to find the overlap.
. Let’s graph these intervals on the number line to find the overlap.
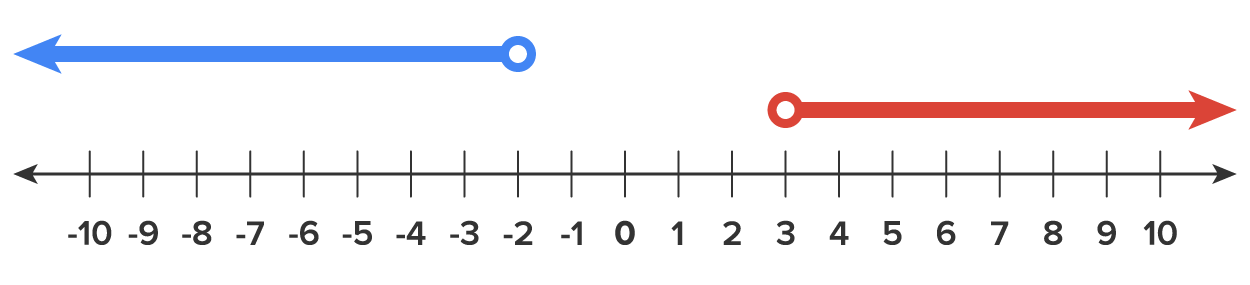
Previously, when learning about set notation, if a value was between two values, we wrote the set, for example, as {x | x > 5 and x ≤ 8}. This indicates that x is a value between 5 and 8. We will learn to write this inequality as a single inequality called a compound inequality. In a compound inequality, when our variable (or expression containing the variable) is between two numbers, we can write it as a single math sentence with three parts, such as 5 less than x less than or equal to 8, to show x is between 5 and 8 (or equal to 8), or 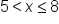 .
.
EXAMPLE
Solve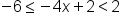 . Write in interval notation and graph the solution.
. Write in interval notation and graph the solution.
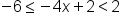
|
The compound inequality |
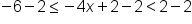
|
Subtract 2 from all 3 parts of the inequality. |
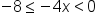
|
Isolate the variable by addressing the coefficient attached to the variable. |
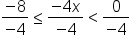
|
Divide all sides by -4. |
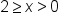
|
Flip all the inequality signs because you are dividing by a negative. |
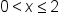
|
Rearrange the inequality so the numbers are in increasing order. |
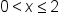 . This means that x can be any value that is greater than 0 and less than or equal to 2.
. This means that x can be any value that is greater than 0 and less than or equal to 2.
| Compound Inequality | |
|---|---|
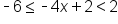
| |
| Solutions | |
|
Set notation: {x | 0 < x ≤ 2} |
Interval notation: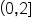
|
| Graph on the number line | |

| |
EXAMPLE
Most beagles have shoulder heights between 36 and 41 centimeters. The following compound inequality relates the estimated shoulder height (in centimeters) of a dog to the internal dimension of the skull D (in cubic centimeters):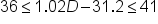
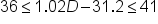
|
The compound inequality |
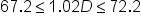
|
Isolate the variable 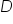 in the middle part by first addressing the constant. Add 31.2 to all 3 parts of the inequality. in the middle part by first addressing the constant. Add 31.2 to all 3 parts of the inequality.
|
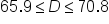
|
Divide all 3 parts by 1.02. Solution rounded to the nearest tenth. |
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License