Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Slope of a Tangent Line Visually

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn what a tangent line is and how to estimate its slope graphically. Specifically, this lesson will cover:

Table of Contents

1. Estimating the Slope of a Tangent Line Graphically

A tangent line is a line that touches a graph at one specific point (but does not cross it).

EXAMPLE

The graph of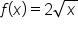 f open parentheses x close parentheses equals 2 square root of x and its tangent line at 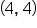open parentheses 4 comma space 4 close parentheses are shown below. Use this picture to estimate the slope of the tangent line.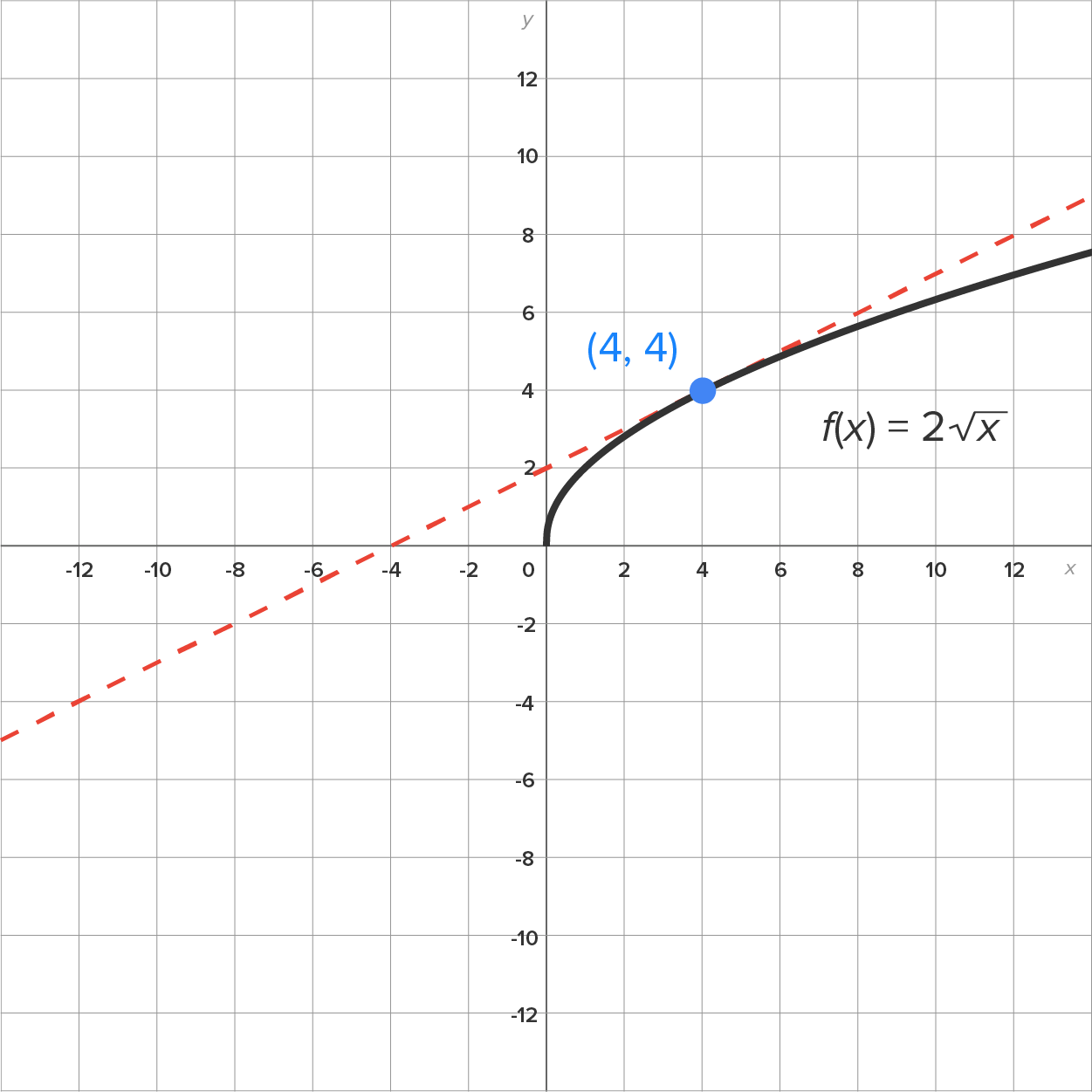

A graph with an x-axis and a y-axis ranging from −12 to 12 in increments of 2. A parabolic portion, representing the function f(x) equals 2 square root x, begins at the origin, passes through a marked point at (4, 4), and extends upward into the first quadrant. A dashed line (tangent line) slants upward from the third quadrant to the first quadrant and passes through the marked point at (4, 4), indicating the point where the line and the parabolic portion touch. The line is tangent to the parabolic portion at the marked point (4, 4).

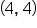In order to estimate the slope of a line, two points are needed. Thus, we need another point on the line besides open parentheses 4 comma space 4 close parentheses to estimate the slope of this line. Inspecting closely, it looks like the point 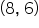open parentheses 8 comma space 6 close parentheses is also contained on the line.

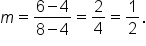Thus, the slope of the tangent line is approximately m equals fraction numerator 6 minus 4 over denominator 8 minus 4 end fraction equals 2 over 4 equals 1 half. In fact, this is the exact slope of the tangent line.

step by step
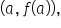If you are given the graph of a function and want to estimate the slope of a tangent line at open parentheses a comma space f open parentheses a close parentheses close parentheses comma do the following:
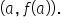
  1. Sketch the tangent line at the point open parentheses a comma space f open parentheses a close parentheses close parentheses.
  2. Find another point on the line. Visually, it is easiest if the point has whole number coordinates, but sometimes this isn’t possible.
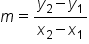  3. Use the slope formula m equals fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction to compute the slope of the line.

try it
Consider the graph of f open parentheses x close parentheses below with its tangent line at the point open parentheses 1 comma space 3 close parentheses.

A graph with an x-axis ranging from −6 to 6 and a y-axis ranging from −5 to 6. The graph has a curve and a dashed line. The curve rises from the third quadrant to the second quadrant by passing through the point (−4, −4), peaks at (0, 3.5), and then extends downward into the fourth quadrant by passing through the marked point at (1, 3). The dashed line slants downward from the second quadrant, passes through the marked point at (1, 3), and then extends into the fourth quadrant by crossing the point (4, 0). The line is tangent to the curve at the point (1, 3).

Identify another point that is on the tangent line.
There are several options, such as open parentheses 2 comma space 2 close parentheses comma open parentheses 3 comma space 1 close parentheses comma and open parentheses 4 comma space 0 close parentheses.
Find the slope of the tangent line.
Using the slope formula with the points open parentheses 1 comma space 3 close parentheses and open parentheses 4 comma space 0 close parentheses comma the slope is m equals fraction numerator 0 minus 3 over denominator 4 minus 1 end fraction equals short dash 3 over 3 equals short dash 1.

term to know
Tangent Line
A line that touches (but does not cross) the graph of a function at a specific point.

2. Horizontal Tangent Lines

Tangent lines whose slopes are 0, also known as horizontal tangent lines, are very useful in calculus. It is important (and quite simple) to identify the places on a graph where the tangent line is horizontal.

EXAMPLE

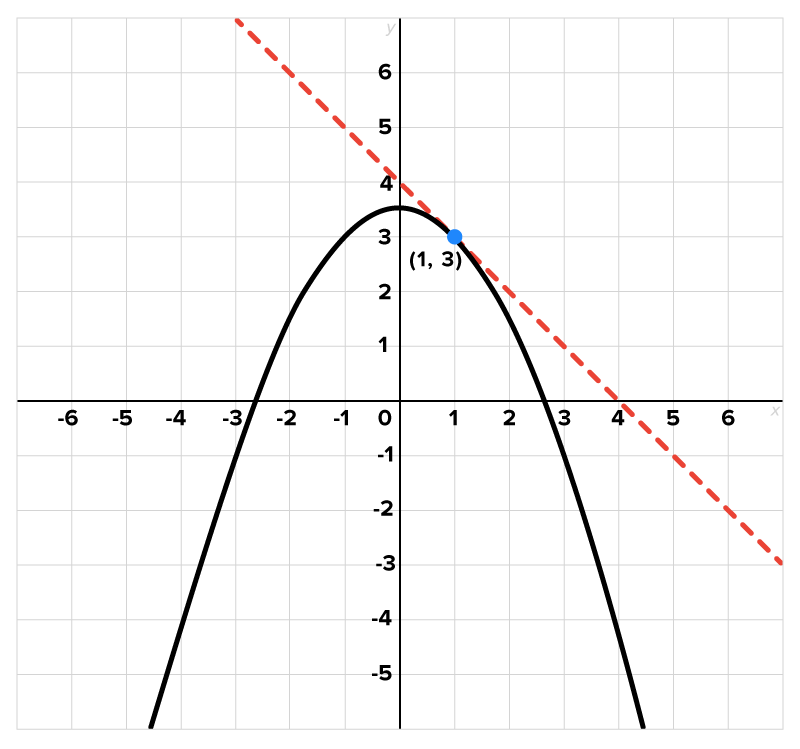
Estimate the slope of the tangent line to the curve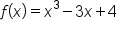 f open parentheses x close parentheses equals x cubed minus 3 x plus 4 at the point 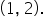open parentheses 1 comma space 2 close parentheses. The graph of f open parentheses x close parentheses and its tangent line are shown here:

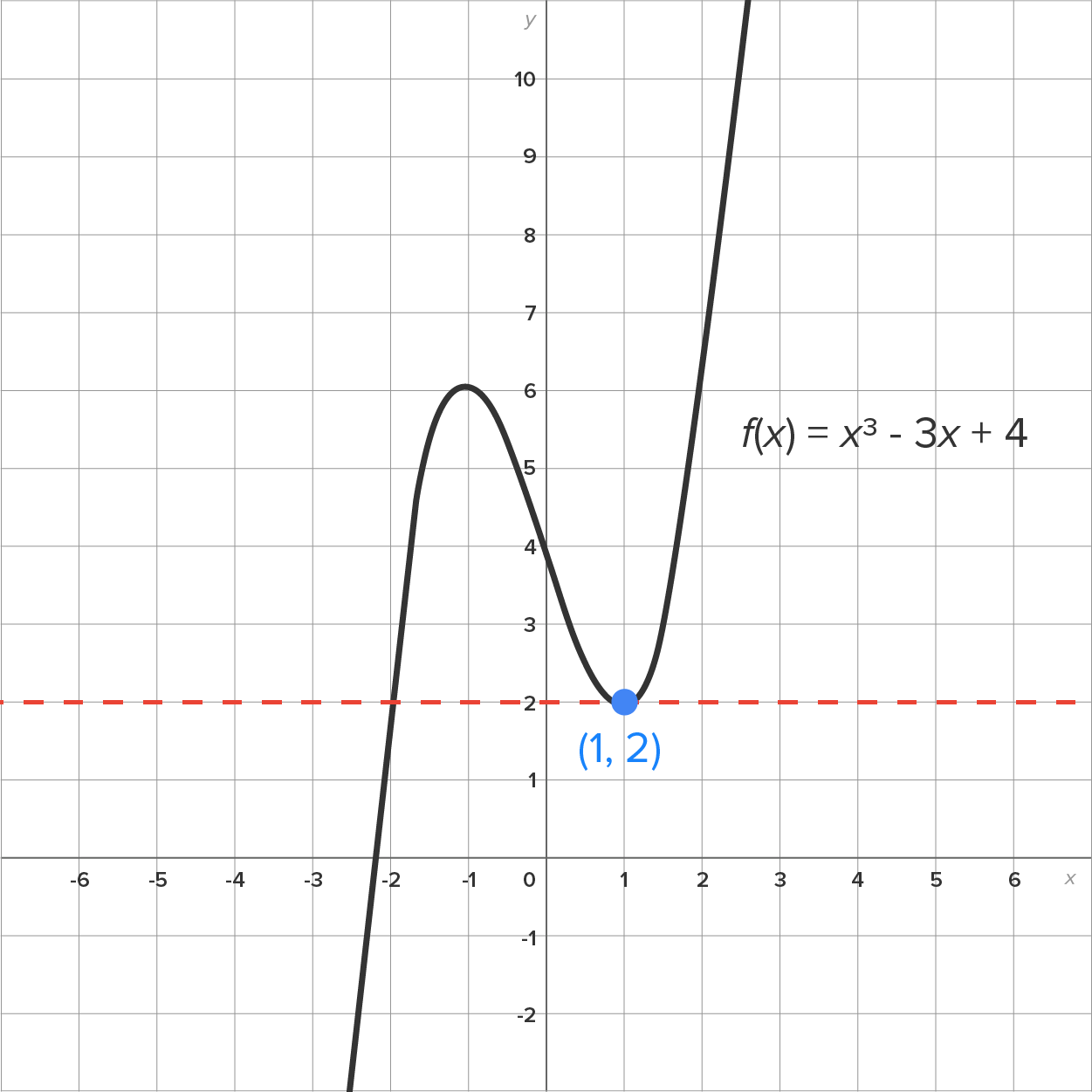
A graph with an x-axis ranging from −6 to 6 and a y-axis ranging from −2 to 10. A curve representing the function f(x) equals x cubed – 3x + 4 rises from the third quadrant, curves downward, and passes through the point (0, 4). It continues downward, reaching the marked point at (1, 2) before rising again into the first quadrant. A horizontal dashed line (tangent line) passes through the marked point at (1, 2). The line is tangent to the curve at the marked point (1, 2).

The tangent line appears to be horizontal, which means its slope is zero.

EXAMPLE

Estimate all values of x for which the graph of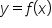 y equals f open parentheses x close parentheses below has a horizontal tangent line.

A graph with an x-axis and a y-axis ranging from −6 to 6. A curve rises steeply from the third quadrant, reaches a peak corresponding to a value of −2.5 on the x-axis by passing through the x-axis between the points −5 and −4, then descends through the y-axis approximately at (0,1), reaches an inverted peak corresponding to a value of 2.5 on the x-axis, and then extends into the first quadrant by crossing the x-axis at (4, 0).

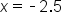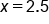Looking at the graph, the values of x for which the tangent lines are horizontal are about x equals short dash 2.5 and x equals 2.5.

summary
In this lesson, you learned about tangent lines, which are lines that touch (but do not cross) the graph of a function at a specific point. You learned that given the graph of a function, you can visually estimate the slope of the tangent line graphically. This can be accomplished by estimating another point on the tangent line. You also learned that tangent lines whose slopes are 0 are known as horizontal tangent lines; these are very useful in calculus.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 0 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Tangent Line

A line that touches (but does not cross) the graph of a function at a specific point.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.