This lesson introduces the likelihood of something happening by discussing simple probability. We will also explore how calculating probability further strengthens our results driven skill. Specifically, this lesson will cover:
- The Difference Between Outcomes and Events
- Probability Theory
- Determining Probability
1. The Difference Between Outcomes and Events
As we have discussed earlier, we are exposed to probabilities on a daily basis. For example, what is the probability of winning a bet, getting the flu, or a small car accident? When discussing “probability,” there are a couple key terms we need to understand first. In probability, we define an outcome as the singular result of some random process.
-
EXAMPLE
When you roll a die, the number facing up is the outcome, such as 1 or 6, etc. There is only one, singular result.
Outcomes will be different based on the process:
-
|
Random Process
|
Outcome
|
|
Die rolling
|
Rolling a 5
|
|
Flipping a coin
|
Tails
|
|
Spinning the wheel on Wheel of Fortune
|
"Bankrupt" (one of the sectors on the wheel)
|
There's a difference between an outcome and an event. While outcomes only have one result, events can have multiple results.
-
|
Random Process
|
Event
|
Outcome
|
|
Die rolling
|
Rolling an even number
|
Rolling a 2, 4, or 6
|
|
Flipping a coin
|
Tails
|
Tails
|
|
Spinning the wheel on Wheel of Fortune
|
Sector over $500
|
"$1,500"
|
For example, when rolling a die, while an outcome would be a 5, an event could be rolling an even number. That consists of the outcomes 2, 4, and 6.
It could be that an event has one outcome in it, like with the coin flipping: an outcome would be tails, but maybe tails is also considered an event. This is an event with one outcome in it.
On the Wheel of Fortune example, for an event such as a sector over $500, there are several outcomes possible.
-
-
- Outcome
- The singular result of a chance experiment.
- Event
- An outcome or set of outcomes.
2. Probability Theory
Now that we understand the difference between an event and the outcome of an event, we can discuss probability. When you conduct a random process once, like spinning a wheel, rolling a die, or flipping a coin, that's called a trial.
The likelihood of a particular event occurring when you do one version of a random process, or “trial,” is called a probability. A probability is expressed as a fraction or decimal number between 0 and 1. Events with probabilities closer to 1 are more likely to occur than events with probabilities closer to 0.
A graph of probability might look like this:
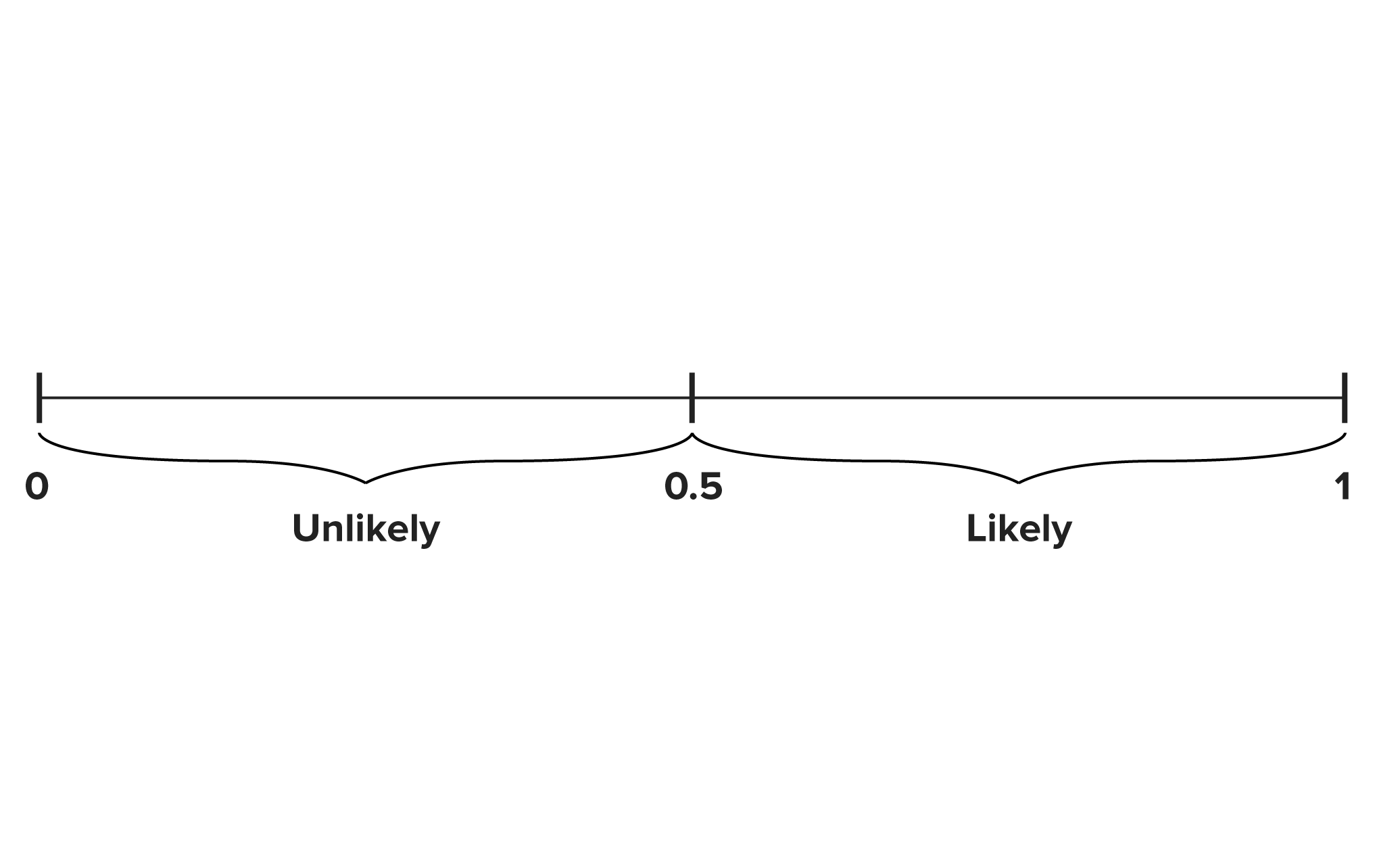
The number in the center, which is 0.5, is considered neither likely nor unlikely. It's equally likely to occur as not occur.
-
What are some events that would fall on this spectrum, from unlikely to likely? Some possible examples might be:
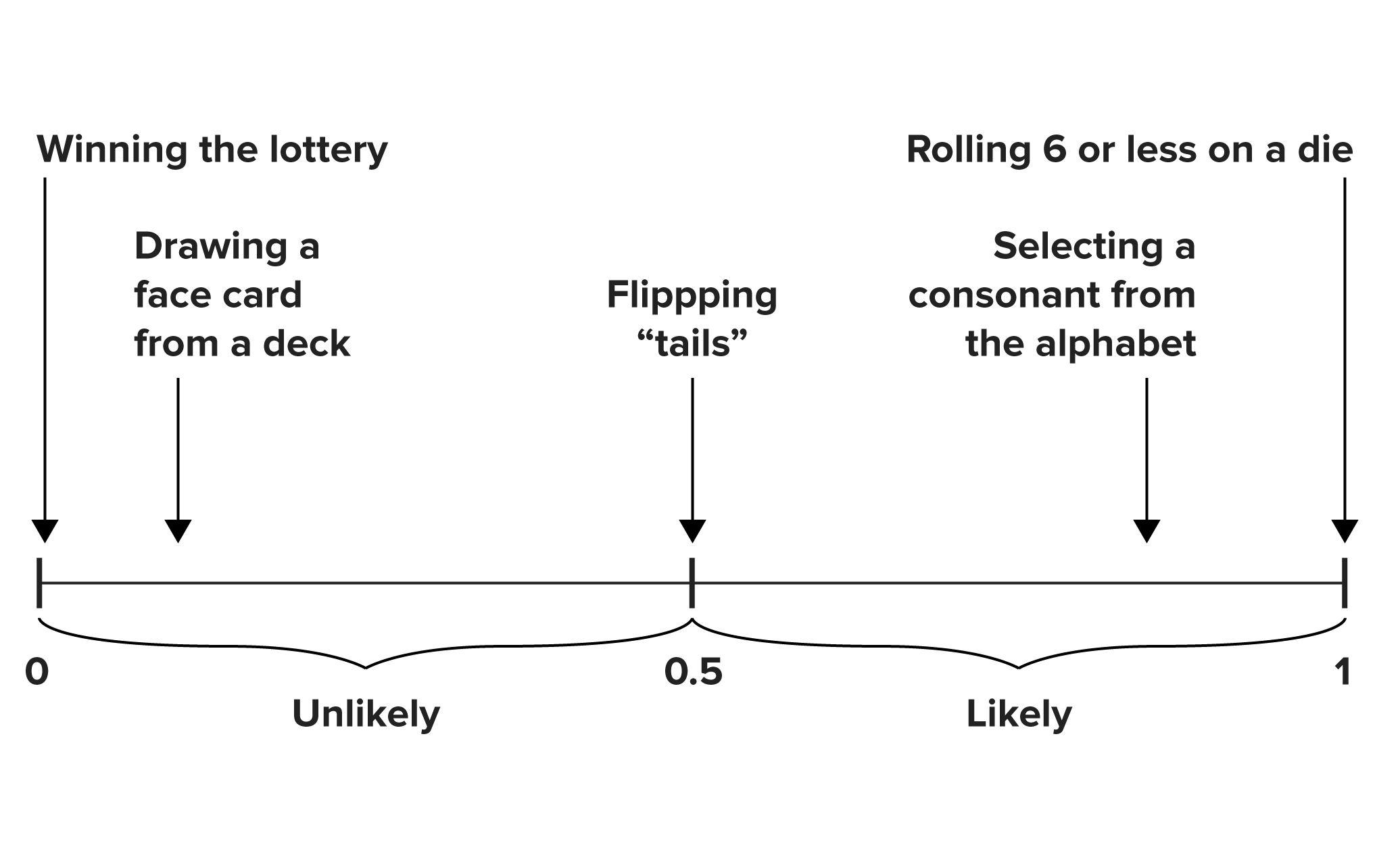
- Winning the lottery has a very low probability—almost zero. A zero probability indicates that the event is impossible. It could not happen. An event with a probability close to zero is extremely unlikely, so it is at the farthest left here.
- Drawing a face card from a deck of cards is further to the left because it is less likely. There are fewer face cards than non-face cards, which means that it would be unlikely to pick a face card.
- Flipping tails on the coin is in the center. There are just as many ways to get tails as not getting tails (or flipping a heads), so we're going to say that flipping coins numerically has a probability of ½, or 0.5.
- Randomly selecting a consonant (e.g., b, c, x) from the alphabet, on the other hand, is quite likely. There are more consonants in the alphabet than vowels (e.g., a, e, i, o), which means it would be likely to pick a consonant. The probability would be plotted further to the right.
- To have the highest probability, 1, you need an event that is certain to happen. The numbers on a die are between 1 and 6. Rolling 6 or less on a die has to happen—the die result has to be the number 6 or less than that. Therefore, this goes on the farthest right.
Take a moment to think about when you may need to calculate probability of achieving a desired outcome in your professional or personal life. You may think of this frequently, but haven’t yet known how to actually determine the probability.
-
-
- Trial
- Running a chance experiment once (e.g., rolling a die, spinning a spinner, flipping a coin).
- Probability
- A number between 0 and 1 that denotes the likelihood of an event. Events with probabilities closer to 1 are more likely to occur than events with probabilities closer to 0.
3. Determining Probability
So now that we know that probability is the likelihood of an event, let’s discuss how to mathematically find the probability of an event occurring. Probability is written as a fraction with the number of favorable outcomes as the numerator and the total number of outcomes as the denominator.
-
-
- Probability of An Event
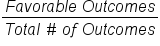
-
EXAMPLE
What is the probability of flipping a coin tails side up?

A coin has 2 sides, heads and tails. First, we want to determine what we consider a favorable outcome. In this case, flipping a tail is the favorable outcome. Because the coin only has a heads or a tails side, there is only one way to get a favorable outcome and land on tails. So, the number in the numerator is 1. As we said, there are only 2 sides to the coin. The number in the denominator is 2. The probability of flipping a coin tails side up is ½.
-
EXAMPLE
You’ve gotten a small box of chocolates. Each of the chocolates are filled with something: 3 with raspberry, 2 with coconut, 3 with caramel, and 4 with dark chocolate. The problem is, you can’t tell which chocolate is which. What is the probability of eating a chocolate with raspberry filling?

Simplify your fraction:
-
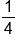
To determine the probability, we need to identify the favorable outcome. In this case, selecting a chocolate with a raspberry filling is the favorable outcome. Out of all the chocolates, there are 3 that have raspberry. So, the number of favorable outcomes for choosing a raspberry filling is 3. This is the numerator of our fraction. The total number of outcomes would be the total number of chocolates in the box. We can determine this by adding the number of each type of chocolate:
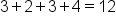
chocolates. So, the denominator or the total number of outcomes is 12. Our probability is
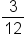
. Remember, probability can be considered a fraction. We need to reduce our fractions to simplest form. So,
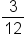
reduces to
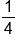
. The probability of eating a chocolate filled with raspberry is
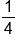
.
-
What is the probability of rolling a 5 on a die?

-
You need to get dressed, but don’t want to turn the light on and wake up your spouse. Assuming all of your socks feel the same, what is the probability that you will successfully pull out a pair of black socks for work if you have 5 pairs of black, 3 pairs of tan, 4 pairs of white, and 1 pair with a dinosaur on it?

In this lesson, we learned about probability. Probability theory discusses the ways to mathematically determine likelihood. Probability is a way to determine how likely certain outcomes or events are when you run a trial of a chance experiment. The difference between outcomes and events is that outcome is the singular result of one trial, whereas an event could be many outcomes, or results, of a single trial. A probability is a fraction of favorable outcomes divided by the total number of outcomes. Determining probability strengthens your results driven skill by calculating how likely your desired goal is to be achieved.
Best of luck in your learning!


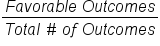


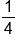
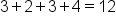 chocolates. So, the denominator or the total number of outcomes is 12. Our probability is
chocolates. So, the denominator or the total number of outcomes is 12. Our probability is 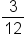 . Remember, probability can be considered a fraction. We need to reduce our fractions to simplest form. So,
. Remember, probability can be considered a fraction. We need to reduce our fractions to simplest form. So, 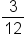 reduces to
reduces to 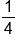 . The probability of eating a chocolate filled with raspberry is
. The probability of eating a chocolate filled with raspberry is 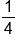 .
.

