Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Savings With Regular Deposits

Author: Sophia Tutorial
PDF Version

what's covered
In this lesson, we’ll work with investments that comprise regular deposits into an account that pays interest, with the goal of finding the future value of those deposits after a specific amount of time. We will also explore how to find the deposit needed in order to meet some future investment goal. Specifically, we will discuss:

Table of Contents

1. Investments With Regular Deposits

Periodically contributing to a savings or investment account is a great way to increase your wealth, prepare for unexpected emergencies, or plan for the future.

One way in which to save money is to use an annuity, which is a sequence of periodic deposits or payments.

EXAMPLE

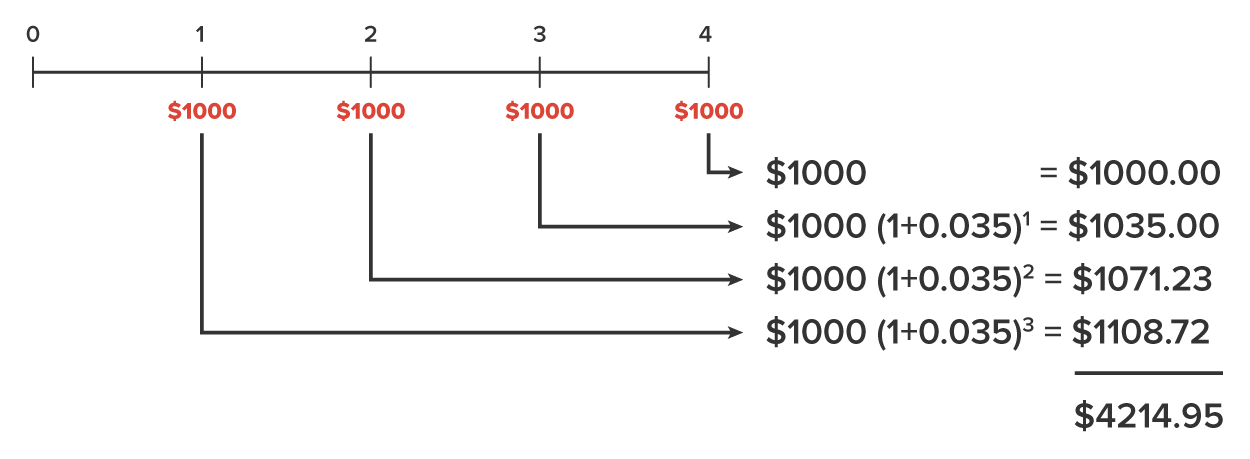
An investment consists of $1,200 deposits at the end of each year. This account gains 3.5% interest each year, applied at the end of the year. Our goal is to compute the amount available in the account immediately after the fourth deposit is made.

The following diagram shows the series of deposits at the end of each year for 4 years.

A timeline labeled ‘Year’ depicting years ranging from 0 to 4. Years 1 to 4 correspond to an amount of $1,000 each.

How much money will be available immediately after the fourth deposit is made?

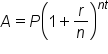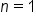We’ll look at this by tracking each individual deposit. Recall that the formula A equals P open parentheses 1 plus r over n close parentheses to the power of n t end exponent is used to find the amount in an account after t years when P dollars has been invested into an account that pays an annual interest rate of r, compounded n times per year. When interest is compounded once per year, n equals 1. 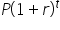This simplifies the formula to P open parentheses 1 plus r close parentheses to the power of t.

Now, let’s find the future value of each deposit at the end of the fourth year.

Here is a diagram to show how long each deposit is in the account.

A timeline labeled ‘Year’ depicting years ranging from 0 to 4. Years 1 to 4 correspond to an amount of $1,000 each. Arrows pointing from Years 1 to 4 represent the interest earned on their respective deposits: Year 1 represents $1,000 (1 plus 0.035) raised to the power of 3 equals $1,108.72, Year 2 represents $1,000 (1 plus 0.035) raised to the power of 2 equals 1,071.23, Year 3 represents $1,000 (1 plus 0.035) raised to the power of 1 equals 1,035.00, and Year 4 represents $1,000 equals $1,000 (indicating no interest earned). The total accumulated amount at the end of Year 4 is $4,214.95.

What's happening in this diagram:
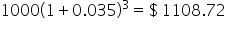  • The first $1,000 deposit is in the account for 3 years. Therefore, its value is 1000 left parenthesis 1 plus 0.035 right parenthesis cubed equals $ 1108.72.
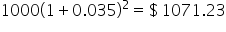  • The second $1,000 deposit is in the account for 2 years. Its value is 1000 left parenthesis 1 plus 0.035 right parenthesis squared equals $ 1071.23.
  • The third $1,000 deposit is in the account for 1 year. Its value is $1,035.
  • The last deposit doesn’t gain any interest at all, so its value is $1,000.

Initiative: Skill in Action
Perhaps these formulas appear foreign to you at the moment, but they play an integral role in investments! When you use your initiative and this content, you're able to better plan for the future. For example, you'll be able to find what monthly or yearly contributions you must make to a retirement account to be able to retire by a certain time. Or perhaps, you might use this formula to start planning for your children's future college fund. Is there something that you want to start saving for now?

While the process to find the amount available is fairly straightforward, it is also tedious for situations with more deposits. For example, what if you were making 20 yearly deposits? That would mean calculating 20 values, then adding them together. For this situation, we can use a formula.

Let’s look back at the previous example to get some ideas:

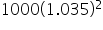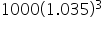The values of each deposit at the end of 4 years were 1000, 1000(1.035), 1000 left parenthesis 1.035 right parenthesis squared, and 1000 left parenthesis 1.035 right parenthesis cubed. Notice that the only thing that changes between two consecutive terms is the exponent on the 1.035, which means that to get from one term to the next, we multiply by 1.035. A sequence that is formed by doing this is called a geometric sequence, and the constant number that is multiplied to each term to get the next term is called the common ratio.

There are special rules we can use to find the sum of the terms of a geometric sequence, and in turn, a formula for the value of a series of deposits immediately after the last deposit is made.

formula to know
Future Value of an Annuity
table attributes columnalign left end attributes row cell S subscript n equals P open square brackets fraction numerator left parenthesis 1 plus r right parenthesis to the power of n minus 1 over denominator r end fraction close square brackets end cell row cell w h e r e colon end cell row cell n equals T h e space n u m b e r space o f space a n n u a l space d e p o s i t s end cell row cell S subscript n equals T h e space f u t u r e space v a l u e space o f space t h e space a n n u i t y space j u s t space a f t e r space t h e space l a s t space d e p o s i t space i s space m a d e end cell row cell r equals T h e space a n n u a l space i n t e r e s t space r a t e end cell row cell P equals T h e space y e a r l y space d e p o s i t divided by p a y m e n t end cell end table

EXAMPLE

If you make annual deposits of $10,000 into a retirement account at the end of each year for the next 30 years, how much will be in the account right after the last deposit is made? Assume an annual interest rate of 2.5%.
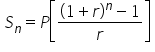
table attributes columnalign left end attributes row cell S subscript n equals P open square brackets fraction numerator left parenthesis 1 plus r right parenthesis to the power of n minus 1 over denominator r end fraction close square brackets end cell end table The future value formula for an annuity.
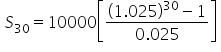
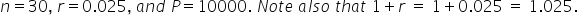
table attributes columnalign left end attributes row cell S subscript 30 equals 10000 open square brackets fraction numerator left parenthesis 1.025 right parenthesis to the power of 30 minus 1 over denominator 0.025 end fraction close square brackets end cell end table Substitute n equals 30 comma space r equals 0.025 comma space a n d space P equals 10000. space N o t e space a l s o space t h a t space 1 plus r space equals space 1 plus 0.025 space equals space 1.025.
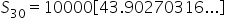
S subscript 30 equals 10000 open square brackets 43.90270316... close square brackets Compute the quantity in brackets.
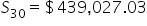
S subscript 30 equals $ 439 comma 027.03 Simplify.

try it
Yearly deposits of $4,500 are placed into an account at the end of each year for 8 years.
How much is available immediately after the 8th deposit? Assume an annual interest rate of 1.3%.
table attributes columnalign left end attributes row cell S subscript n equals P open square brackets fraction numerator left parenthesis 1 plus r right parenthesis to the power of n minus 1 over denominator r end fraction close square brackets end cell end table The future value formula for an annuity.
table attributes columnalign left end attributes row cell S subscript 8 equals 4500 open square brackets fraction numerator left parenthesis 1.013 right parenthesis to the power of 8 minus 1 over denominator 0.013 end fraction close square brackets end cell end table Substitute n equals 8 comma space r equals 0.013 comma space a n d space P equals 4500. space N o t e space a l s o space t h a t space 1 plus r space equals space 1 plus 0.013 space equals space 1.013.
S subscript 8 equals 4500 open square brackets 8.3736194... close square brackets Compute the quantity in brackets.
S subscript 8 equals $ 37 comma 681.29 Simplify.

$37,681.29 will be available in the account immediately after making the 8th annual deposit.

think about it
In the previous example, notice that eight deposits of $4,500, or $36,000, is required from the investor to have $37,681.29 at the end of 8 years. The difference between these two quantities is the interest earned, which in this case is $1,681.29.

terms to know
Annuity
A series of payments that are equal and made at regular intervals (yearly, monthly, etc.).
Geometric Sequence
A list of numbers in which the first term is given, and each subsequent term is obtained by multiplying the previous term by the same number.
Common Ratio
In a geometric sequence, this is the number that each term is multiplied by to get the next term.

2. Annuities With Multiple Deposits Per Year

Not all investments are made up of yearly deposits. One example is a retirement account in which deposits are made monthly. The formula 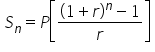table attributes columnalign left end attributes row cell S subscript n equals P open square brackets fraction numerator left parenthesis 1 plus r right parenthesis to the power of n minus 1 over denominator r end fraction close square brackets end cell end table can be adapted to annuities in which deposits are made more than once per year, as long as the interest rate, r, and number of payments, n, are adjusted as well.

EXAMPLE

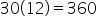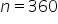Suppose an annuity consists of monthly deposits for 30 years, where the annual interest rate is 1.2%, compounded monthly. Then, there are 30 left parenthesis 12 right parenthesis equals 360 deposits, meaning n equals 360.
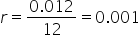In addition, the monthly interest rate is r equals fraction numerator 0.012 over denominator 12 end fraction equals 0.001.


EXAMPLE

After opening a Roth IRA, you decide that you can afford to deposit $100 into your account at the end of each month for the next 25 years. If the annual interest rate stays steady at 1.5%, compounded monthly, how much will be available in this account after the last deposit is made?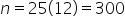

Noting that the payments into the account form an annuity, also keep in mind that the payments are made monthly.

First, find the number of payments and the interest rate per month:
  • The number of payments is n equals 25 left parenthesis 12 right parenthesis equals 300.
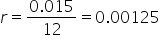  • The interest rate per month is r equals fraction numerator 0.015 over denominator 12 end fraction equals 0.00125.
We are now ready to apply the future value formula.
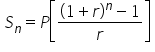
table attributes columnalign left end attributes row cell S subscript n equals P open square brackets fraction numerator left parenthesis 1 plus r right parenthesis to the power of n minus 1 over denominator r end fraction close square brackets end cell end table The future value formula for an annuity.
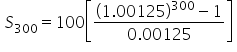
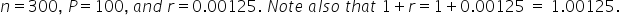
table attributes columnalign left end attributes row cell S subscript 300 equals 100 open square brackets fraction numerator left parenthesis 1.00125 right parenthesis to the power of 300 minus 1 over denominator 0.00125 end fraction close square brackets end cell end table Substitute n equals 300 comma space P equals 100 comma space a n d space r equals 0.00125. space N o t e space a l s o space t h a t space 1 plus r equals 1 plus 0.00125 space equals space 1.00125.
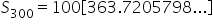
S subscript 300 equals 100 open square brackets 363.7205798... close square brackets Evaluate the quantity in brackets.
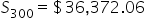
S subscript 300 equals $ 36 comma 372.06 Evaluate completely.

You'll have $36,372.06 available at the end of the 25 years.


try it
A retirement account is set up with quarterly deposits of $800 at the end of each quarter for the next 15 years.
How much is available after the last deposit, assuming an annual interest rate of 2.2%, compounded quarterly?
Noting that the payments into the account form an annuity, also keep in mind that the payments are made quarterly (four times per year).

Find the number of payments and quarterly interest rate:
  • The number of payments is n equals 15 left parenthesis 4 right parenthesis equals 60.
  • The interest rate per quarter is r equals fraction numerator 0.022 over denominator 4 end fraction equals 0.0055.
We are now ready to apply the future value formula.
table attributes columnalign left end attributes row cell S subscript n equals P open square brackets fraction numerator left parenthesis 1 plus r right parenthesis to the power of n minus 1 over denominator r end fraction close square brackets end cell end table The future value formula for an annuity.
table attributes columnalign left end attributes row cell S subscript 60 equals 800 open square brackets fraction numerator left parenthesis 1.0055 right parenthesis to the power of 60 minus 1 over denominator 0.0055 end fraction close square brackets end cell end table Substitute n equals 60 comma space P equals 800 comma space a n d space r equals 0.0055. space N o t e space a l s o space t h a t space 1 plus r equals 1 plus 0.0055 space equals space 1.0055.
S subscript 60 equals 800 open square brackets 70.58654595... close square brackets Evaluate the quantity in brackets.
S subscript 60 equals $ 56 comma 685.24 Evaluate completely.

Thus, $56,685.24 is available at the end of the 15 years.

3. Finding the Periodic Deposit in Order to Meet an Investment Goal

There are situations where you have an investment goal in the future and want to know the payment connected to that goal. The same formula is used; we’ll just need to solve that formula for P.

EXAMPLE

Suppose that in 40 years, you will want a lump sum of $800,000 available to you for retirement. What monthly payment is required to meet this goal, assuming an annual interest rate of 2.01%, compounded monthly?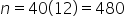

Noting that the payments into the account form an annuity, also keep in mind that the payments are made monthly.

This means the following:
  • The number of payments is n equals 40 left parenthesis 12 right parenthesis equals 480.
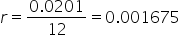  • The interest rate per month is r equals fraction numerator 0.0201 over denominator 12 end fraction equals 0.001675.
We are now ready to apply the future value formula.
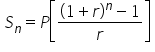
table attributes columnalign left end attributes row cell S subscript n equals P open square brackets fraction numerator left parenthesis 1 plus r right parenthesis to the power of n minus 1 over denominator r end fraction close square brackets end cell end table The future value formula for an annuity.
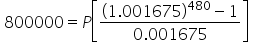
table attributes columnalign left end attributes row cell 800000 equals P open square brackets fraction numerator left parenthesis 1.001675 right parenthesis to the power of 480 minus 1 over denominator 0.001675 end fraction close square brackets end cell end table Substitute 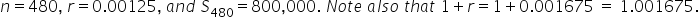n equals 480 comma space r equals 0.00125 comma space a n d space S subscript 480 equals 800 comma 000. space N o t e space a l s o space t h a t space 1 plus r equals 1 plus 0.001675 space equals space 1.001675.
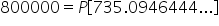
800000 equals P open square brackets 735.0946444... close square brackets Evaluate the quantity in brackets.
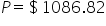
P equals $ 1086.82 Divide by 736.0946444 to solve for P.

You will need to invest $1,086.82 monthly to have $800,000 available in 40 years.


try it
In planning for a child, parents wish to set up an account in which quarterly deposits are made at the end of every 3 months for 20 years.
Assuming an annual interest rate of 1.8%, compounded quarterly, what quarterly deposit is required so that $30,000 is available in the account 20 years from now?
Noting that the payments into the account form an annuity, also keep in mind that the payments are made quarterly (four times per year).

Find the number of payments and the interest rate per quarter:
  • The number of payments is n equals 20 left parenthesis 4 right parenthesis equals 80.
  • The interest rate per quarter is r equals fraction numerator 0.018 over denominator 4 end fraction equals 0.0045.
We are now ready to apply the future value formula.
table attributes columnalign left end attributes row cell S subscript n equals P open square brackets fraction numerator left parenthesis 1 plus r right parenthesis to the power of n minus 1 over denominator r end fraction close square brackets end cell end table The future value formula for an annuity.
table attributes columnalign left end attributes row cell 30000 equals P open square brackets fraction numerator left parenthesis 1.0045 right parenthesis to the power of 80 minus 1 over denominator 0.0045 end fraction close square brackets end cell end table Substitute n equals 80 comma space r equals 0.0045 comma space a n d space S subscript 80 equals 30000. space N o t e space a l s o space t h a t space 1 plus r equals 1 plus 0.0045 space equals space 1.0045.
30000 equals P open square brackets 96.038301396... close square brackets Evaluate the quantity in brackets.
P equals $ 312.38 Divide both sides by 96.038301396 to solve for P.

So, you will need to invest $312.38 each quarter to have $30,000 available in 20 years.

summary
In this lesson, you learned that periodically contributing to a savings or investment account is a great way to save money, for a variety of reasons. You learned how to model the growth of such an account by calculating investments with regular deposits and later by using a specific formula. You also explored examples that had annuities made with multiple deposits in a year and how to find the periodic deposits needed to meet an investment goal.

Best of luck in your learning!

Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.

Terms to Know
Annuity

A series of payments that are equal and made at regular intervals (yearly, monthly, etc.)

Common Ratio

In a geometric sequence, this is the number that each term is multiplied by to get the next term.

Geometric Sequence

A list of numbers in which the first term is given, and each subsequent term is obtained by multiplying the previous term by the same number.

Formulas to Know
Future Value of an Annuity

table attributes columnalign left end attributes row cell S subscript n equals P open square brackets fraction numerator left parenthesis 1 plus r right parenthesis to the power of n minus 1 over denominator r end fraction close square brackets end cell row cell w h e r e colon end cell row cell n equals T h e space n u m b e r space o f space a n n u a l space d e p o s i t s end cell row cell S subscript n equals T h e space f u t u r e space v a l u e space o f space t h e space a n n u i t y space j u s t space a f t e r space t h e space l a s t space d e p o s i t space i s space m a d e end cell row cell r equals T h e space a n n u a l space i n t e r e s t space r a t e end cell row cell P equals T h e space y e a r l y space d e p o s i t divided by p a y m e n t end cell end table

© 2026 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.