Table of Contents |
When you take a sample, it is important to try to obtain values that are accurate and represent the true values for the population. A measure of an attribute of a sample is called a sample statistic
EXAMPLE
In election season, suppose we took a simple random sample of 500 people from a town of 10,000 and found that in this particular poll, 285 of those 500 plan to vote for Candidate Y. That would mean that our best guess for the proportion of the town that will vote for Candidate Y, when the election actually does happen, is 285 out of 500, or 57%. This 57% is a sample statistic.In general, the following notations are for the sample statistics that we generate most often. The sample proportion is shown as p-hat. The sample mean is shown as x-bar. Lastly, a sample standard deviation is shown as s.
| Sample Statistic Examples (Statistics) |
|---|
Sample proportion = 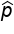
|
Sample Mean = 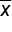
|
Sample Std Dev = 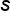
|
A sample statistic is a measurement from a sample, and a population parameter is the corresponding measurement for the population. This is something that we can find in a sample. The only way to figure out a parameter is to take a census.
EXAMPLE
In our previous example, the sample proportion was 57%. The population proportion, however, is unknown; we won't know it until election day. In applied statistics, it is often a goal to use sample statistics to better understand unknowable population parameters.| Statistic | Parameter |
|---|---|
| Sample Proportion = 57% | Population proportion = ? |
A population proportion is denoted as p (without the hat). A population mean is denoted as the Greek letter mu, and a population standard deviation is shown with the Greek letter sigma.
| Population Parameter Examples (Parameters) |
|---|
Population proportion = 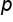
|
Population Mean = 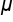
|
Population Std Dev = 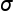
|
IN CONTEXT
The mean GPA of all 2,000 students at a school is 2.9, while the GPA of a sample of 50 students is 3.1
What is the population parameter and the sample statistic?
Based on the information provided, we can identify the following population parameters:
- Population size = 2,000
- Population mean = μ = 2.9
We can also find the following sample statistics:
- Sample size = 50
- Sample mean = x̅ = 3.1
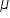 .
.Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.