Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Rolle's Theorem

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn about Rolle’s theorem, a seemingly simple yet powerful theorem whose consequences are used in Unit 5 (Antiderivatives). Specifically, this lesson will cover:

Table of Contents

1. Introduction to Rolle’s Theorem

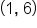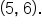
Let’s say we have a function that passes through the points open parentheses 1 comma space 6 close parentheses and open parentheses 5 comma space 6 close parentheses.

try it
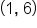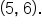Take a piece of paper and draw the points open parentheses 1 comma space 6 close parentheses and open parentheses 5 comma space 6 close parentheses. Connect the two points with a curve that is continuous and differentiable (something other than a horizontal line between them). This means that the graph has no break and no sharp turn.
What do you notice about your curve? Does your curve contain at least one horizontal tangent?
Hopefully you have at least one horizontal tangent. As it turns out, under certain circumstances, this will always happen.

big idea
Rolle’s theorem:
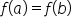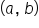Let f open parentheses x close parentheses be continuous on the closed interval open square brackets a comma space b close square brackets with f open parentheses a close parentheses equals f open parentheses b close parentheses, and differentiable on the open interval open parentheses a comma space b close parentheses.

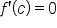Then, there is at least one value of c between a and b for which f apostrophe open parentheses c close parentheses equals 0.

2. Applying Rolle’s Theorem

Now, let’s look at a few examples of how Rolle’s theorem can be applied.

EXAMPLE

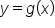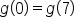Here is the graph of some function y equals g open parentheses x close parentheses, where g open parentheses 0 close parentheses equals g open parentheses 7 close parentheses.

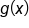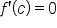Since g open parentheses x close parentheses is continuous and differentiable, it follows by Rolle’s theorem that there is at least one value of c between 0 and 7 where f apostrophe open parentheses c close parentheses equals 0.

A graph with an x-axis and a y-axis ranging from −6 to 6, representing the function y equals g(x). The graph contains a wavy curve that starts from the point (0, 1.1), moves downward to reach the point (2, −1.1), then rises to a peak at the point (4, 2), falls to reach the point (6, 0.5), and then rises again in the first quadrant.

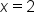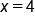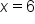In the graph, we can see there are three x-values where a horizontal tangent line occurs: x equals 2, x equals 4, and x equals 6. Therefore, the guaranteed values of c are 2, 4, and 6.

EXAMPLE

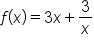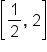Consider the function f open parentheses x close parentheses equals 3 x plus 3 over x on the interval open square brackets 1 half comma space 2 close square brackets.

First, check requirements for Rolle’s theorem.
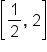f open parentheses x close parentheses is continuous on any interval not including 0, and therefore is continuous on open square brackets 1 half comma space 2 close square brackets.
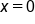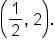
f open parentheses x close parentheses is differentiable everywhere except where x equals 0, so f open parentheses x close parentheses is certainly differentiable on open parentheses 1 half comma space 2 close parentheses.
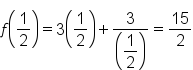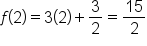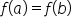f open parentheses 1 half close parentheses equals 3 open parentheses 1 half close parentheses plus fraction numerator 3 over denominator open parentheses begin display style 1 half end style close parentheses end fraction equals 15 over 2 and f open parentheses 2 close parentheses equals 3 open parentheses 2 close parentheses plus 3 over 2 equals 15 over 2. Therefore, f open parentheses a close parentheses equals f open parentheses b close parentheses.
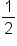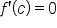Thus, the conditions of Rolle’s theorem have been met and there is at least one value of c between 1 half and 2 such that f apostrophe open parentheses c close parentheses equals 0.

To find all values of c, take the derivative, then set equal to 0, then solve.

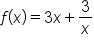
f open parentheses x close parentheses equals 3 x plus 3 over x Start with the original function.
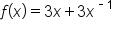
f open parentheses x close parentheses equals 3 x plus 3 x to the power of short dash 1 end exponent Rewrite to use the power rule.
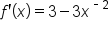
f apostrophe open parentheses x close parentheses equals 3 minus 3 x to the power of short dash 2 end exponent Take the derivative.
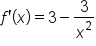
f apostrophe open parentheses x close parentheses equals 3 minus 3 over x squared Rewrite with positive exponents.
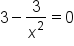
3 minus 3 over x squared equals 0 Set equal to 0.
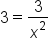
3 equals 3 over x squared Add 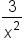3 over x squared to both sides.
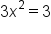
3 x squared equals 3 Multiply both sides by 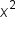x squared.
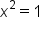
x squared equals 1 Divide both sides by 3.
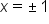
x equals plus-or-minus 1 Take the square root of both sides.

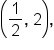Since we want all values on the interval open parentheses 1 half comma space 2 close parentheses comma the value guaranteed by Rolle's theorem is 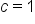c equals 1. (In other words, since 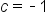c equals short dash 1 is not on the interval 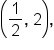open parentheses 1 half comma space 2 close parentheses comma it is not considered.)

watch
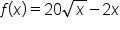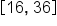In this video, we will find all values of c guaranteed by Rolle’s theorem for f open parentheses x close parentheses equals 20 square root of x minus 2 x on the interval open square brackets 16 comma space 36 close square brackets.

summary
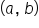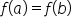In this lesson, you learned that when a function is continuous on a closed interval open square brackets a comma space b close square brackets, differentiable on the open interval open parentheses a comma space b close parentheses, and f open parentheses a close parentheses equals f open parentheses b close parentheses, then Rolle’s theorem guarantees that there is a value of c between a and b such that 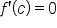f apostrophe open parentheses c close parentheses equals 0, which means that there is a guaranteed horizontal tangent line at c. Then, you examined a few examples involving the application of Rolle's theorem.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 3 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.