Table of Contents |
With the exception of multiples of 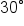 and
and 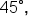 most other function values are more convenient to use when approximated by using your calculator.
most other function values are more convenient to use when approximated by using your calculator.
Your calculator should have buttons labeled “SIN,” “COS,” and “TAN.” To evaluate one of these functions at a specific angle, it is important to make sure that your calculator is set to the appropriate angle mode.
Degree mode: the angle input of a sine or cosine function is treated as a degree measure. For example, when you evaluate 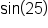 on your calculator, you will get the value of
on your calculator, you will get the value of 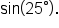
Radian mode: the angle input of a sine or cosine function is treated as a radian measure. For example, when you evaluate 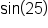 on your calculator, the angle is measured in radians.
on your calculator, the angle is measured in radians.
EXAMPLE
Using a calculator, we’ll approximate the following values to four decimal places.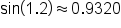 (The angle 1.2 is measured in radians, so be sure to put your calculator in radian mode before evaluating.)
(The angle 1.2 is measured in radians, so be sure to put your calculator in radian mode before evaluating.)
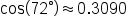 (The angle
(The angle 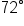 is measured in degrees, so be sure to put your calculator in degree mode before evaluating.)
is measured in degrees, so be sure to put your calculator in degree mode before evaluating.)
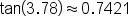 (The angle 3.78 is measured in radians, so be sure to put your calculator in radian mode before evaluating.)
(The angle 3.78 is measured in radians, so be sure to put your calculator in radian mode before evaluating.)
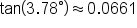 (The angle
(The angle 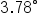 is measured in degrees, so be sure to put your calculator in degree mode before evaluating.)
is measured in degrees, so be sure to put your calculator in degree mode before evaluating.)
Some calculators have an angle feature that allows you to add a “degree” symbol at the end of the angle. If your calculator is in radian mode and you type in 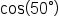 , for example, it will return the cosine function of
, for example, it will return the cosine function of 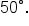 Check to see if your calculator has this feature, and use it if this makes things easier for you. It might be easier than switching the mode all the time.
Check to see if your calculator has this feature, and use it if this makes things easier for you. It might be easier than switching the mode all the time.
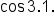
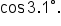
Notice that your calculator does not have the reciprocal functions (secant, cosecant, and cotangent) as dedicated buttons. Remember that each of these functions is the reciprocal of one other trigonometric function. This will help to evaluate function values of secant, cosecant, and cotangent.
EXAMPLE
Evaluate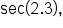
 and
and 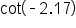 to four decimal places.
to four decimal places.
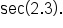
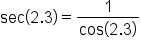
|
Use the identity 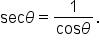
|
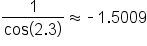
|
Approximate using a calculator. |
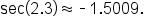
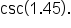

|
Use the identity 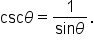
|
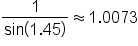
|
Approximate using a calculator. |
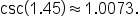

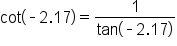
|
Use the identity 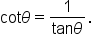
|
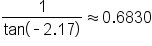
|
Approximate using a calculator. |
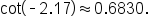
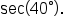
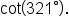
Now that we know how to approximate trigonometric functions of any angle, we are ready to solve application problems that involve right triangles.
Since a triangle’s angles have a sum of 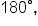 a right triangle has two angles whose sum is
a right triangle has two angles whose sum is 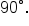 These angles are called complements, and are described as complementary. Since the angles must be positive, they must have measures that are less than
These angles are called complements, and are described as complementary. Since the angles must be positive, they must have measures that are less than 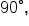 which makes them acute angles.
which makes them acute angles.
Consider the following picture, which shows two circles centered at the origin, with angle 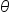 that terminates in the first quadrant.
that terminates in the first quadrant.
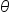 having terminal point
having terminal point 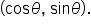
 with angle
with angle 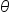 having terminal point
having terminal point 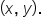
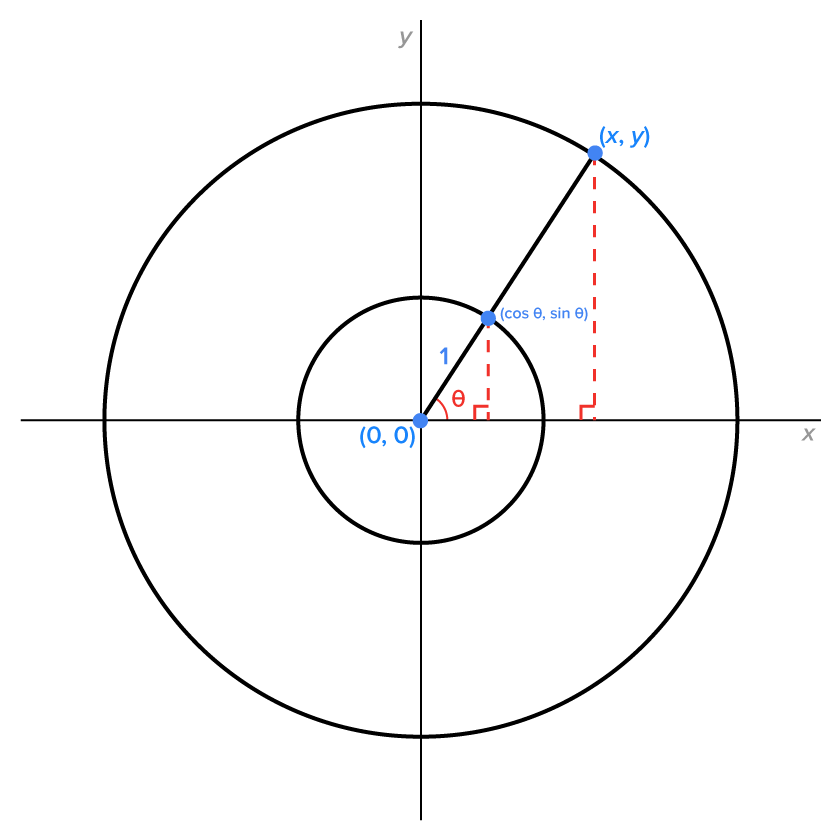
As it turns out, knowing the point 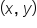 and its distance r from the origin, we can find the values of
and its distance r from the origin, we can find the values of 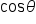 and
and 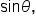 and as a consequence, the value of each of the other trigonometric functions of angle
and as a consequence, the value of each of the other trigonometric functions of angle 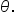
Since the triangle is contained in the first quadrant, we know that 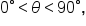 meaning that
meaning that 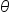 is an acute angle. Note now the similar right triangles that are formed by dropping vertical lines from the points
is an acute angle. Note now the similar right triangles that are formed by dropping vertical lines from the points 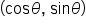 and
and 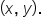
Here is a closer look at these triangles, with the lengths of their sides labeled:

|

|
Since these triangles are similar, we know that the lengths of the corresponding sides are in proportion to one another. This means that the ratio of any two sides in one triangle is equal to the ratio of the same two sides in the other triangle.
Using the base and the hypotenuse of each triangle,  which gives
which gives 
Using the height and hypotenuse from each triangle,  which means
which means 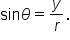
Thus, given that angle 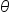 has a terminal side that contains the point
has a terminal side that contains the point 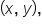
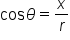 and
and 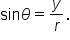
Note: if 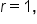 as with the unit circle, we have
as with the unit circle, we have 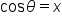 and
and 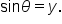
Recall also that 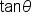 is the slope of the line containing the origin and the terminal point of the angle. It follows that
is the slope of the line containing the origin and the terminal point of the angle. It follows that 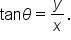
Given a right triangle as shown in the figure, we can find the sine, cosine, and tangent functions of the angle as follows.
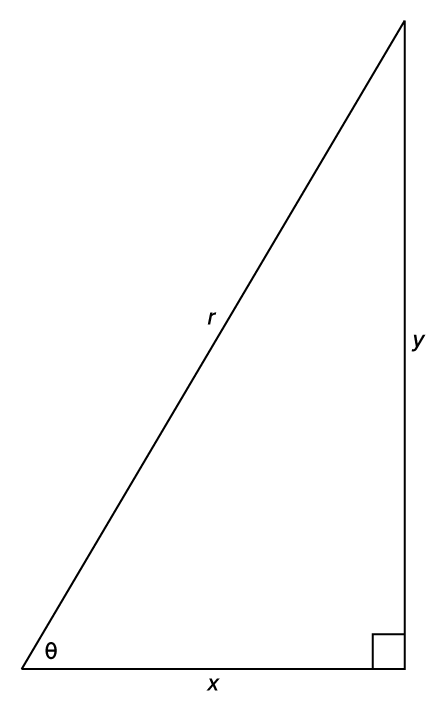
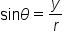

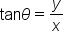
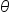 and x is the side adjacent to
and x is the side adjacent to 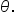 The side r is called the hypotenuse of the triangle.
The side r is called the hypotenuse of the triangle.
Then, we can label the triangle this way.
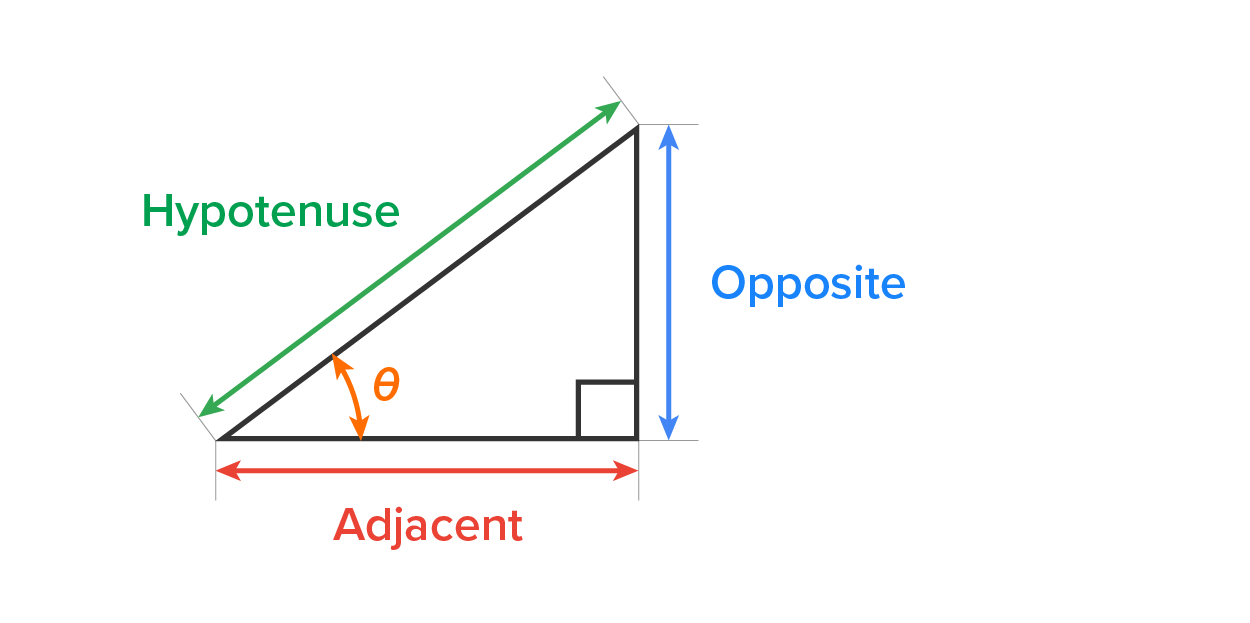
The values of 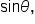
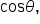 and
and 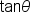 are found as follows:
are found as follows:
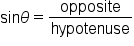
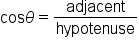

One way to remember these ratios is by the mnemonic “SohCahToa.” The S, C, and T stand for trig functions, and the lowercase letters after each capital letter are the sides that are used to compute the value of each function.
The sine, cosine, and tangent functions are the most commonly used. The value of each of the other trigonometric functions is computed by calculating the appropriate reciprocal.
EXAMPLE
Consider the right triangle shown below.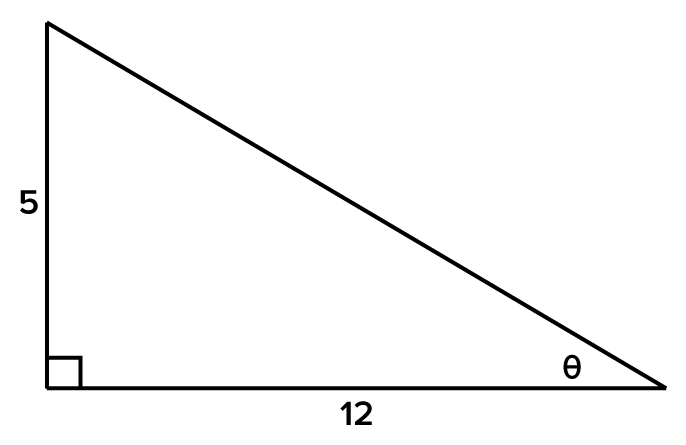
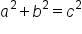
|
This is the Pythagorean theorem, where 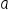 and b are the lengths of the legs and c is the length of the hypotenuse. and b are the lengths of the legs and c is the length of the hypotenuse.
|
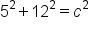
|
Let 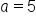 and and 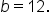
|
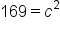
|
Simplify. |
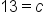
|
Apply the square root property. Since c is the length of a side of a triangle, only the positive solution is considered. |
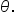
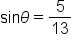
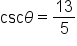
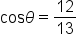
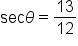
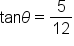
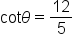
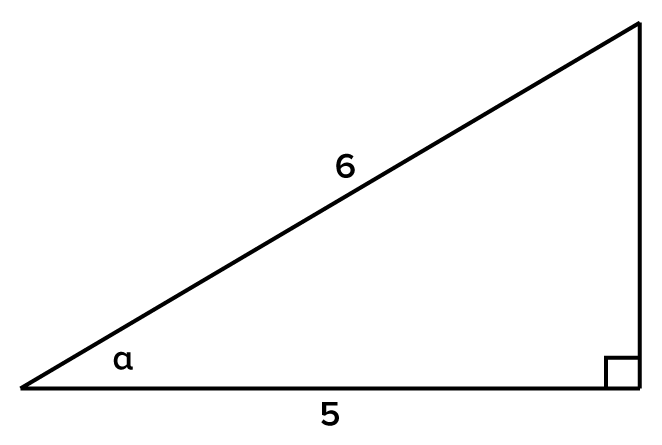
Now we will look at problems in which the measure of an angle is known, and we wish to find the other sides and angles of a triangle.
EXAMPLE
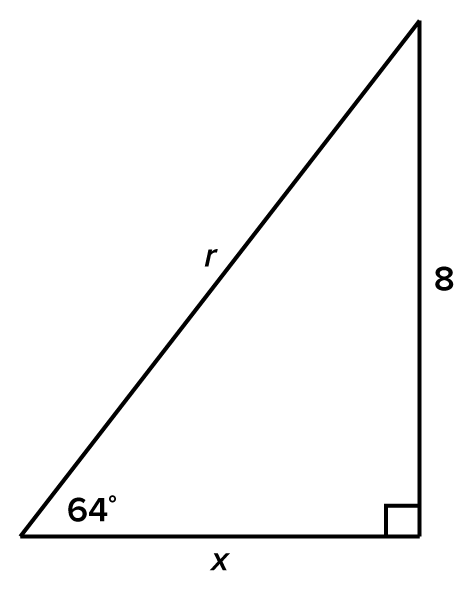
Consider the triangle shown below.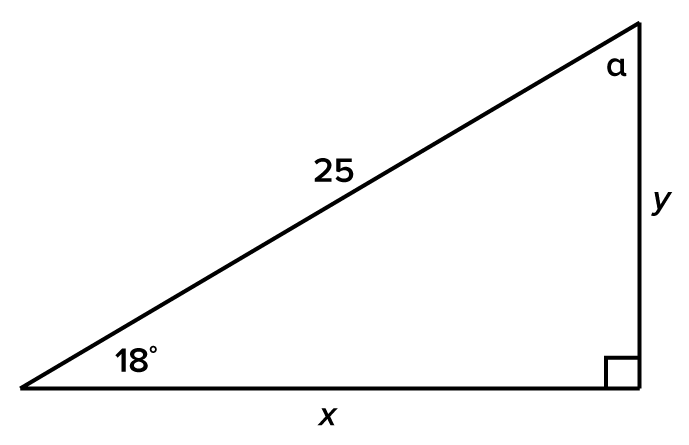
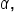 rounded to the nearest whole number.
rounded to the nearest whole number.
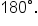 Then,
Then, 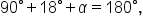 which means
which means 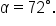
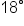 as reference.
as reference.
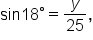
 and
and 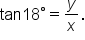 The last equation is not very helpful since it has two variables in it.
The last equation is not very helpful since it has two variables in it.
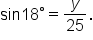
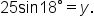 Using a calculator in degree mode,
Using a calculator in degree mode, 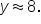
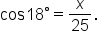
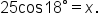 Using a calculator in degree mode,
Using a calculator in degree mode, 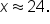
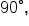 or in radians, their sum is
or in radians, their sum is 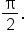
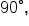 or in radians, less than
or in radians, less than 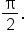
The two acute angles in a right triangle are complementary. It turns out that trigonometric functions of complementary angles are related. Consider the right triangle shown below.
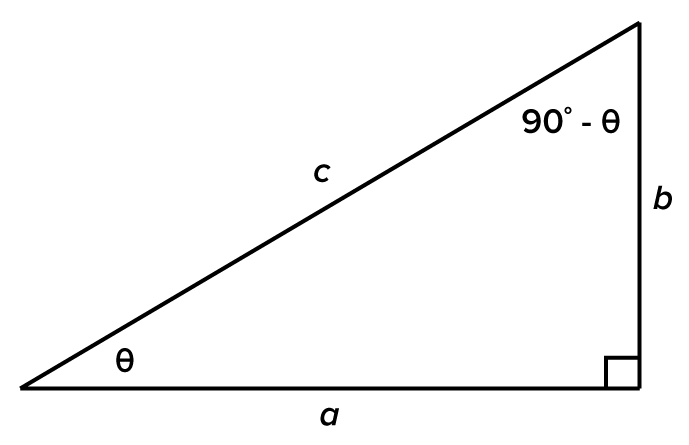
If 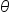 is the measure of one acute angle, then the measure of the other is
is the measure of one acute angle, then the measure of the other is 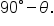
Here are the six trigonometric functions evaluated for 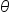 and its complement,
and its complement, 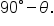
Trigonometric Functions of 
|
Trigonometric Functions of 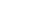
|
|---|---|
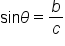
|
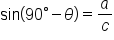
|
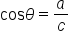
|
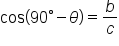
|
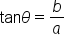
|
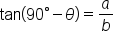
|
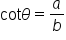
|
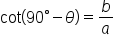
|
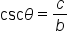
|
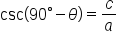
|
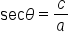
|
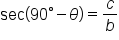
|
By comparing values of the trig functions, we have six pairs of expressions that are equal:

The first two equations tell us that the sine of one angle is the cosine of its complement, and vice versa. The functions sine and cosine are called “cofunctions” since one has a “co” and the other doesn’t. Notice that secant and cosecant are cofunctions, as well as tangent and cotangent.
The main idea is that cofunctions of complementary angles are equal.
One can also write the cofunction identities in terms of radians. To do so, replace 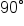 with
with 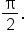
In order to use the cofunction identities effectively, we need to know how to find complementary angles, more specifically with radians.
EXAMPLE
Find the complement of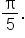
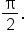
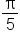 is
is 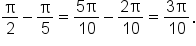
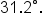
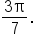
Using complements, we can rewrite trigonometric expressions using cofunction identities.
EXAMPLE
The expressions and
and 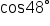 are equal by the cofunction identities, since sine and cosine are cofunctions, and
are equal by the cofunction identities, since sine and cosine are cofunctions, and 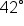 and
and 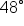 are complements.
are complements.
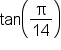 and
and 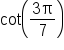 are equivalent since tangent and cotangent are cofunctions, and
are equivalent since tangent and cotangent are cofunctions, and 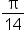 and
and 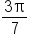 are complements.
are complements.
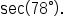
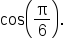
Trigonometric functions are useful in determining the height of very tall objects.
Consider the figure below.
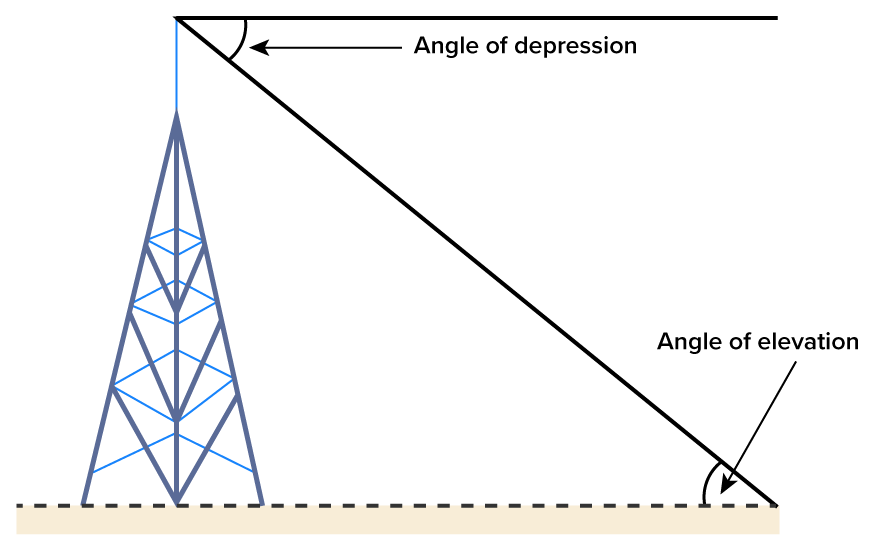
To measure the height of the tower, it would be dangerous to climb the structure with a tape measure in one hand to measure the height. As the picture suggests, one could stand a distance away from the base of the tower and determine the angle of elevation to the top of the building, then use trigonometry to find the height of the building. The angle of depression is made with the horizontal that points downward toward an object
In order to solve problems in this lesson, you’ll need to do the following:
EXAMPLE
From a point 30 feet away from the base of a tree, the angle of elevation to the top of the tree is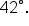 What is the height of the tree, to the nearest foot?
What is the height of the tree, to the nearest foot?

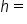 the height of the tree.
the height of the tree.
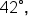 we want to find its opposite side, and we know the length of its adjacent side. This means we should use the tangent function.
we want to find its opposite side, and we know the length of its adjacent side. This means we should use the tangent function.
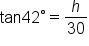
|

|
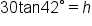
|
Multiply both sides of the equation by 30. |
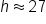
|
Approximate the solution. |
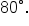
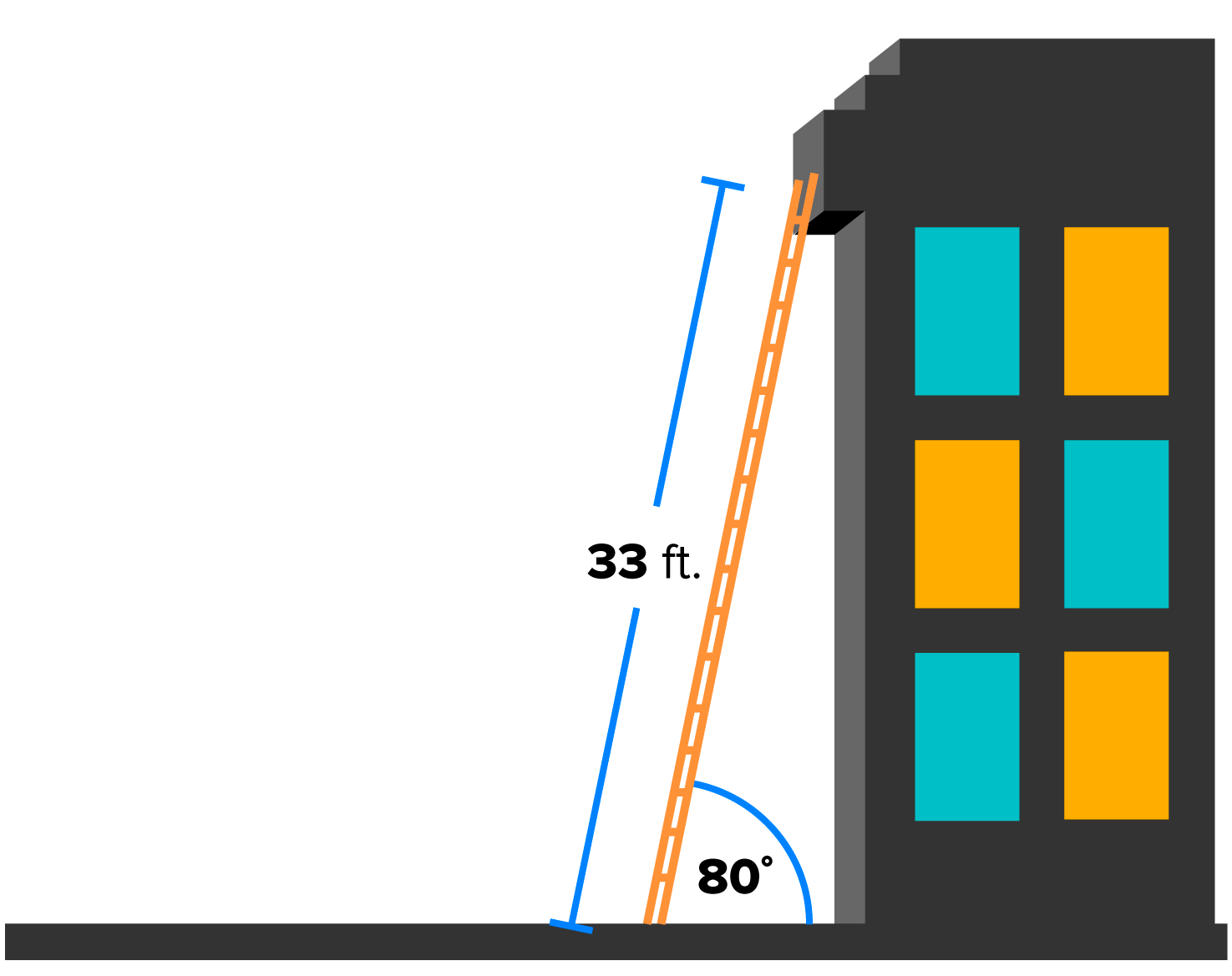
Sometimes two right triangles are needed to solve problems.
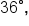 and that the angle of depression to the bottom of the tower is
and that the angle of depression to the bottom of the tower is 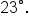 How tall is the tower to the nearest tenth of a foot?
How tall is the tower to the nearest tenth of a foot?
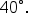 The angle of elevation to the top of the antenna is measured to be
The angle of elevation to the top of the antenna is measured to be 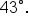
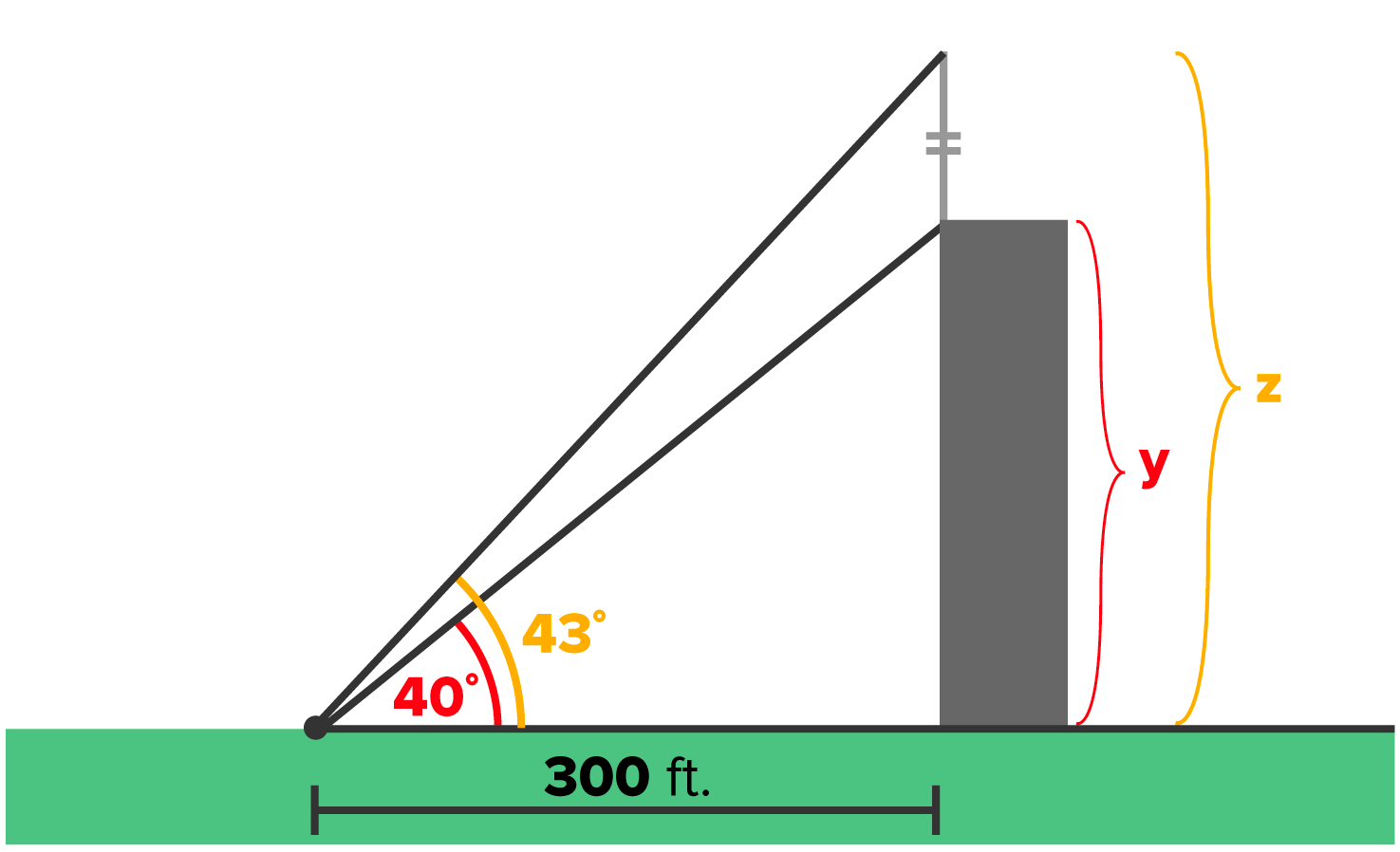
 . Then, you apply the trigonometric functions to right triangles, where the value of a trigonometric function is the ratio of two sides. You also learned that the relationship between the two acute angles in a right triangle (as complementary angles) gives way to the cofunction identities, the main idea being that cofunctions of complementary angles are equal. Finally, you learned that you can solve many real-life problems, particularly with angles of depression and elevation, by using a right triangle as a model.
. Then, you apply the trigonometric functions to right triangles, where the value of a trigonometric function is the ratio of two sides. You also learned that the relationship between the two acute angles in a right triangle (as complementary angles) gives way to the cofunction identities, the main idea being that cofunctions of complementary angles are equal. Finally, you learned that you can solve many real-life problems, particularly with angles of depression and elevation, by using a right triangle as a model.
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.