Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Restricting the Domain to Find Inverse Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will find inverses of functions which require restricting the domain. Specifically, this lesson will cover:

Table of Contents

before you start
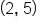Earlier in this course, we talked about functions and their inverses. A function f open parentheses x close parentheses is one-to-one if every point on the graph of f open parentheses x close parentheses has a different y-coordinate. For example, if f open parentheses x close parentheses is one-to-one and the point open parentheses 2 comma space 5 close parentheses is on the graph of 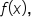f open parentheses x close parentheses comma then there is no other point on the graph of f open parentheses x close parentheses that has a y-coordinate of 5.

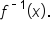When f open parentheses x close parentheses is one-to-one, then f open parentheses x close parentheses has a corresponding inverse function which we call f to the power of short dash 1 end exponent open parentheses x close parentheses. The graphical way to check if a function f open parentheses x close parentheses is one-to-one is the horizontal line test.

In this lesson, we are going to focus on polynomial functions and their inverses.

Here is a problem to help you review these concepts.

try it
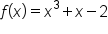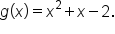
Consider the functions f open parentheses x close parentheses equals x cubed plus x minus 2 and g open parentheses x close parentheses equals x squared plus x minus 2.
Use a graph to determine if f   (x  ) is one-to-one.
Since the graph passes the horizontal line test, f open parentheses x close parentheses is one-to-one.
Use a graph to determine if g   (x  ) is one-to-one.
Since the graph does not pass the horizontal line test, g open parentheses x close parentheses is not one-to-one.

1. Restricting the Domain of a Function So That It Is One-to-One

Now that you have reviewed some important ideas, let’s explore ways to find inverses of functions that are not one-to-one. You have done some extensive work in this course with quadratic functions. As you know, the graph of a quadratic function is a parabola, which is not one-to-one.

In general, when a function f open parentheses x close parentheses is not one-to-one, its domain can be restricted so that it is one-to-one over the restricted domain, and therefore has an inverse function. How is such a domain restriction chosen? Typically, the largest possible domain is chosen. The next few examples with quadratic functions will help to illustrate this.

EXAMPLE

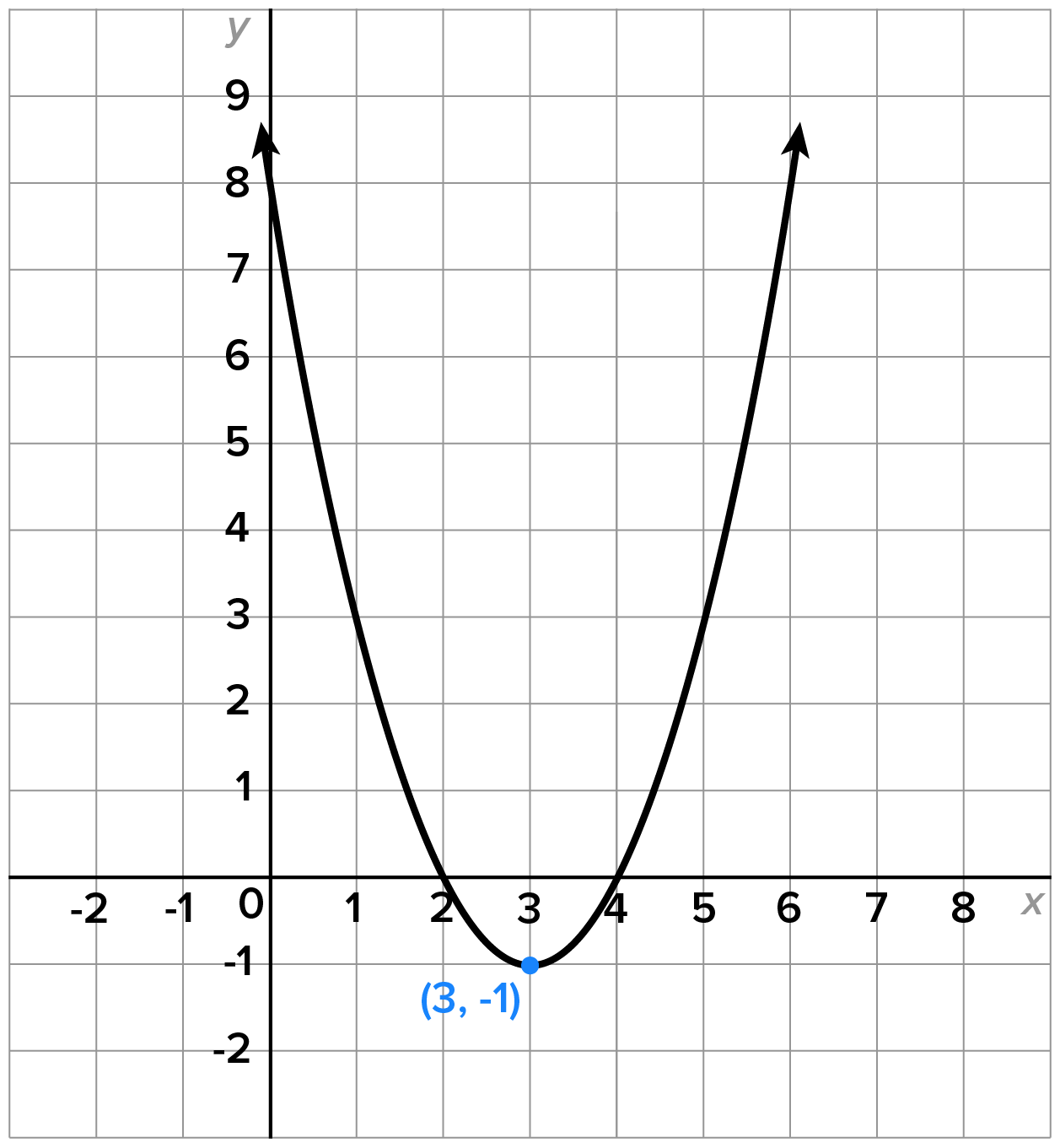
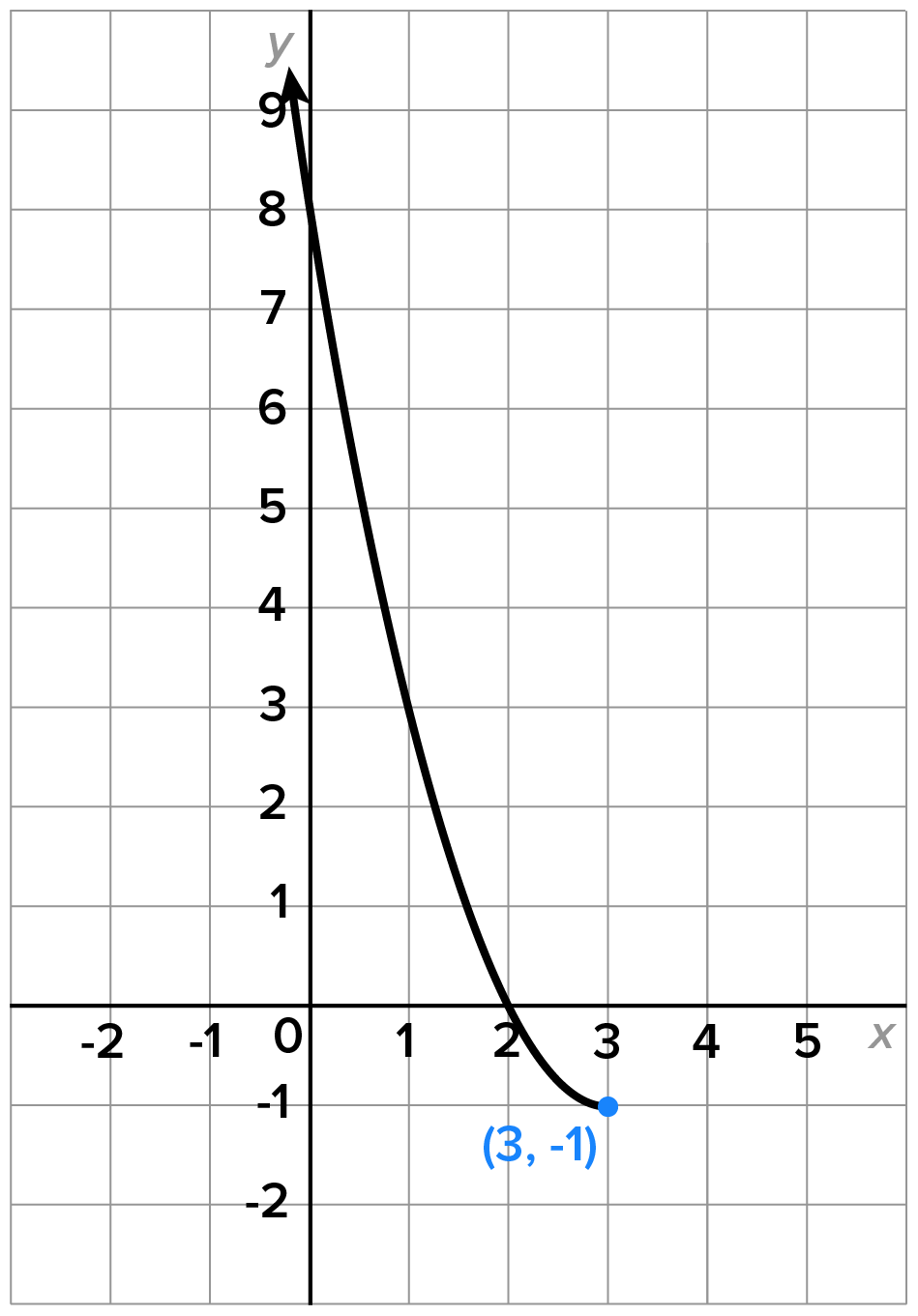
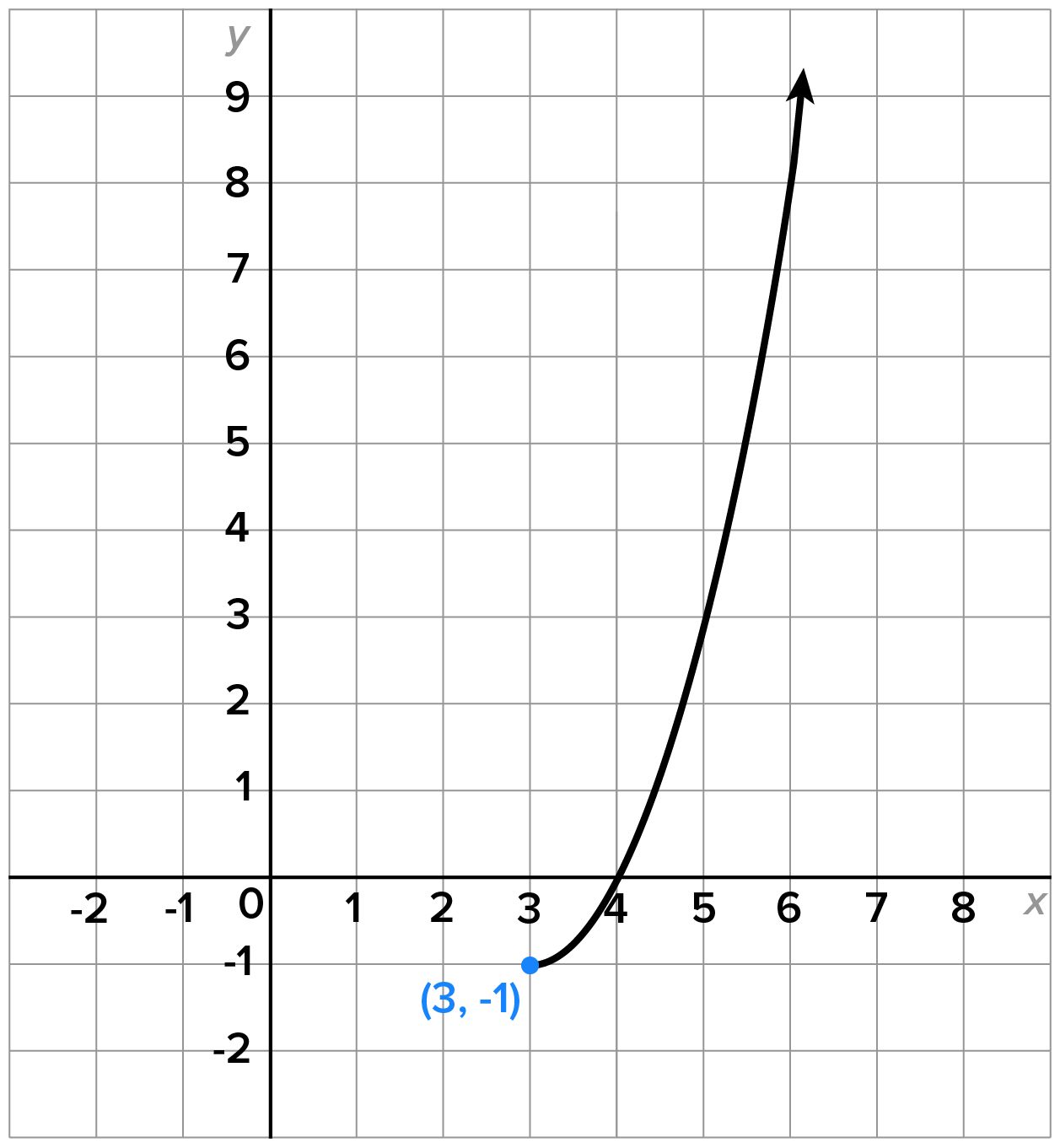
Consider the quadratic function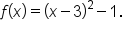 f open parentheses x close parentheses equals open parentheses x minus 3 close parentheses squared minus 1.

Three graphs are shown below.

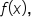  • The leftmost is the graph of f open parentheses x close parentheses comma which is clearly not one-to-one.
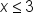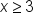  • The next two are graphs with domains restricted to x less or equal than 3 and x greater or equal than 3, respectively.
bold italic f open parentheses bold x close parentheses bold equals open parentheses bold x bold minus bold 3 close parentheses to the power of bold 2 bold minus bold 1 bold italic f open parentheses bold x close parentheses bold equals open parentheses bold x bold minus bold 3 close parentheses to the power of bold 2 bold minus bold 1 bold comma bold space bold italic x bold less or equal than bold 3 bold italic f open parentheses bold x close parentheses bold equals open parentheses bold x bold minus bold 3 close parentheses to the power of bold 2 bold minus bold 1 bold comma bold space bold italic x bold greater or equal than bold 3
A graph with an x-axis ranging from −2 to 8 and a y-axis ranging from −2 to 9. A parabola with vertex (3, -1) opens upward, passing through the points (2, 0) and (4, 0), and (0, 8). A graph with an x-axis ranging from −2 to 5 and a y-axis ranging from −2 to 9.The left half of a parabola with vertex at (3, -1). The graph contains the points (3, -1) as its rightmost point, (2, 0) and (0, 8). A graph with an x-axis ranging from −2 to 8 and a y-axis ranging from −2 to 9. the right half of a parabola with vertex (3, -1) opens upward, passing through the points (4, 0), and (0, 8).

Both domain restrictions are the largest possible domains that can be used for the function to be one-to-one. Note that both graphs pass the horizontal line test.

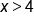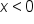In this previous example, there are other restrictions such as x greater than 4 or x less than 0 that would also produce functions that are one-to-one. As we will see later in this course, the largest possible domain restriction is generally desired.

EXAMPLE

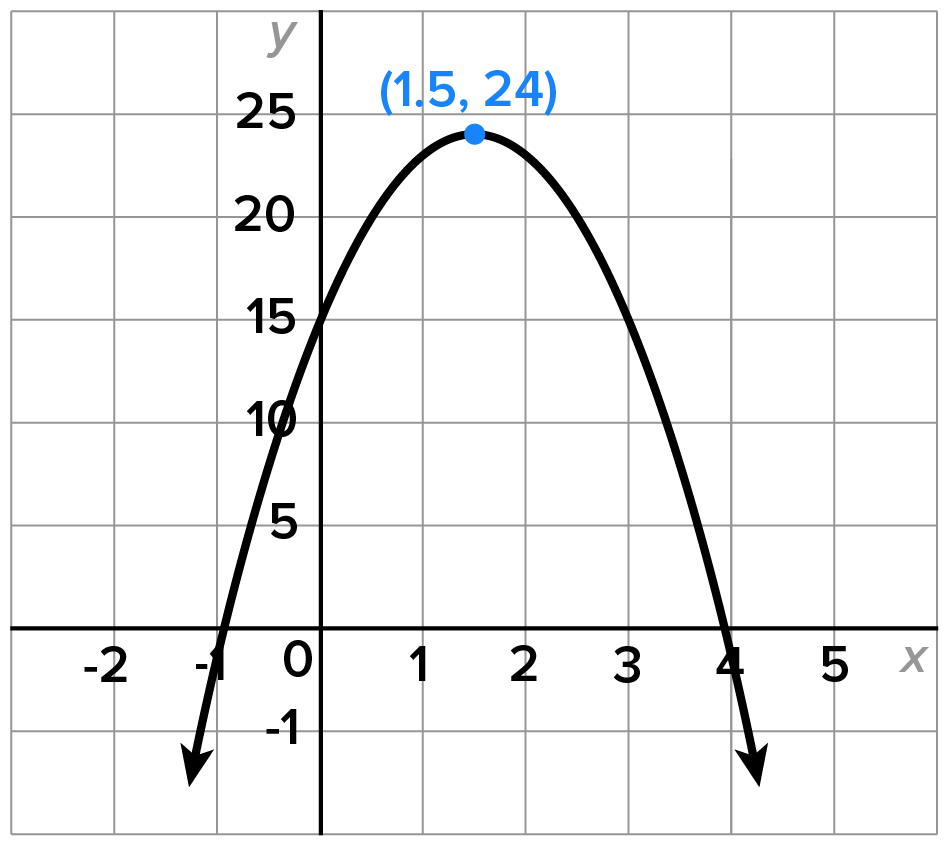
Consider the function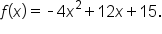 f open parentheses x close parentheses equals short dash 4 x squared plus 12 x plus 15.

The graph of f open parentheses x close parentheses is shown here, and note that it is not one-to-one.

A graph with an x-axis ranging from −2 to 5 and a y-axis ranging from −1 to 25 in increments of 5. A parabola has vertex at (1.5, 24) and opens downward, passing through the points (0, 15), (3, 15), (-1, 0) and (4, 0).

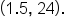
Observe that the vertex is open parentheses 1.5 comma space 24 close parentheses.

To restrict the domain to the largest possible sets of values, there are two possible choices so that the result is a one-to-one function:

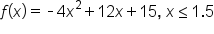
f open parentheses x close parentheses equals short dash 4 x squared plus 12 x plus 15 comma space x less or equal than 1.5
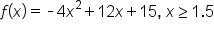
f open parentheses x close parentheses equals short dash 4 x squared plus 12 x plus 15 comma space x greater or equal than 1.5

try it
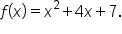
Consider the function f open parentheses x close parentheses equals x squared plus 4 x plus 7.
Restrict the domain of f   (x  ) so that it is one-to-one on the domain.
There are two natural choices: x less or equal than short dash 2 or x greater or equal than short dash 2.

2. Finding the Inverse of Polynomial and Radical Functions

2a. Inverses of Quadratic and Square Root Functions

Now we are ready to find inverses of functions. Before doing so, here are some key things to remember:

  • The domain of a function is the same set of values as the range of its inverse function.
  • The range of a function is the same set of values as the domain of its inverse function.
Before finding the inverse of a polynomial function, determine its domain and range.

EXAMPLE

Consider the function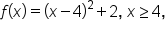 f open parentheses x close parentheses equals open parentheses x minus 4 close parentheses squared plus 2 comma space x greater or equal than 4 comma whose graph is shown below.

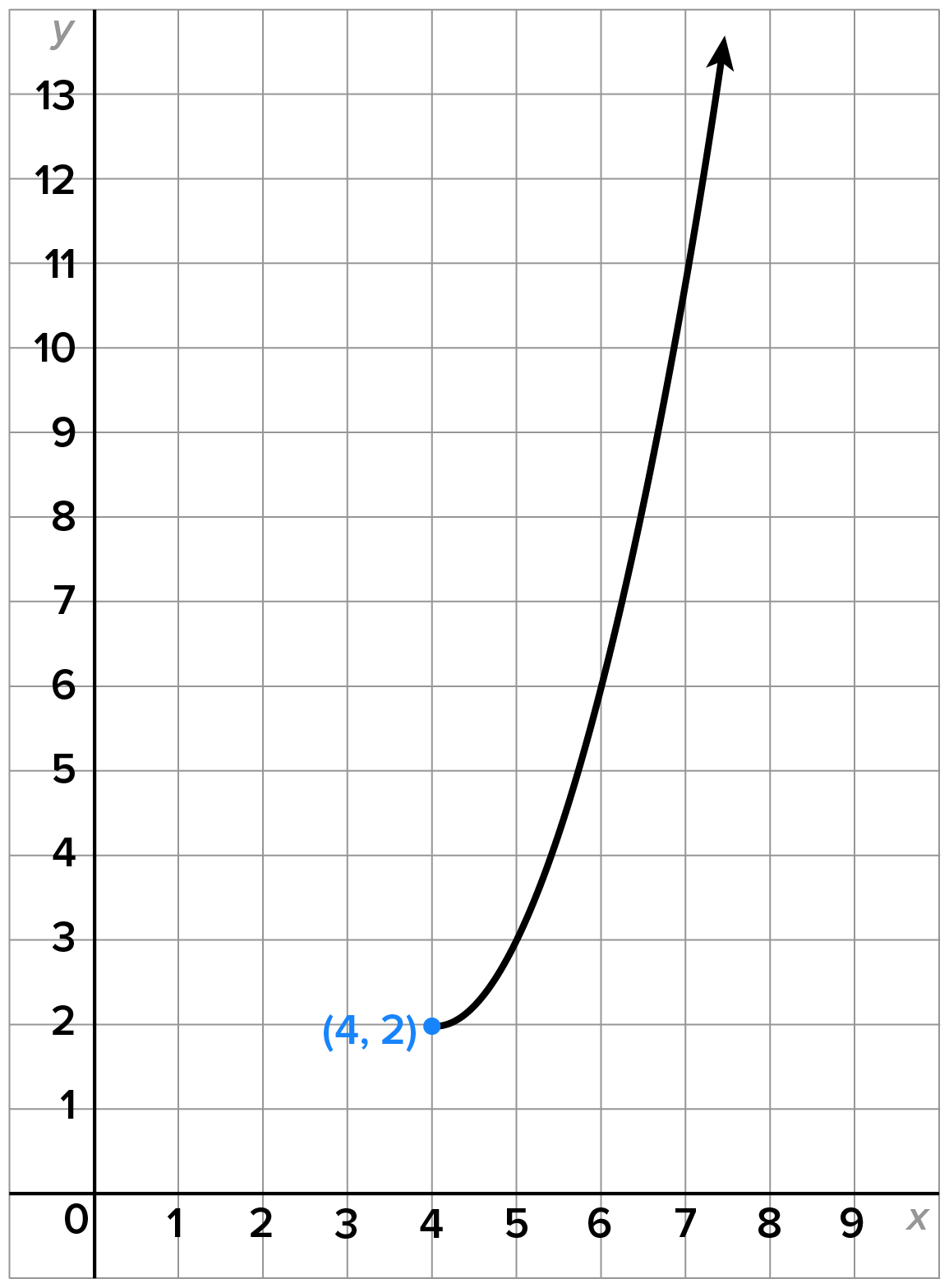
A graph with an x-axis ranging from 0 to 9 and a y-axis ranging from 0 to 13. The right half of a parabola with vertex at (4, 2), which opens upward and passes through the points (5, 3) and (6, 6).

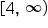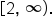
The domain was already given as open square brackets 4 comma space infinity close parentheses, and the range of f open parentheses x close parentheses is open square brackets 2 comma space infinity close parentheses.

Now, let’s find its inverse function.

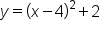
y equals open parentheses x minus 4 close parentheses squared plus 2 Replace f open parentheses x close parentheses with y.
x equals open parentheses y minus 4 close parentheses squared plus 2 Interchange x and y.
x minus 2 equals open parentheses y minus 4 close parentheses squared Subtract 2 from both sides.
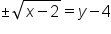
plus-or-minus square root of x minus 2 end root equals y minus 4 Apply the square root principle.
y equals 4 plus-or-minus square root of x minus 2 end root Add 4 to both sides; write y on the left-hand sides.

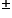Because of the “plus-or-minus”, this is not a function. The domain and range of f open parentheses x close parentheses and its inverse are used to determine if the “+” or “-” is used.

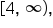Since the domain of f open parentheses x close parentheses is open square brackets 4 comma space infinity close parentheses comma the range of the inverse is also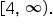 open square brackets 4 comma space infinity close parentheses.

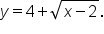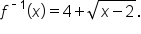
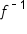Since a square root always returns a positive value, adding the square root to 4 will produce numbers that are 4 or greater. Thus, the inverse is y equals 4 plus square root of x minus 2 end root. This can now be written using function notation, so we can formally say that the inverse is f to the power of short dash 1 end exponent open parentheses x close parentheses equals 4 plus square root of x minus 2 end root.

The graphs of f and f to the power of short dash 1 end exponent are shown in the graph, along with the line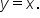 y equals x.

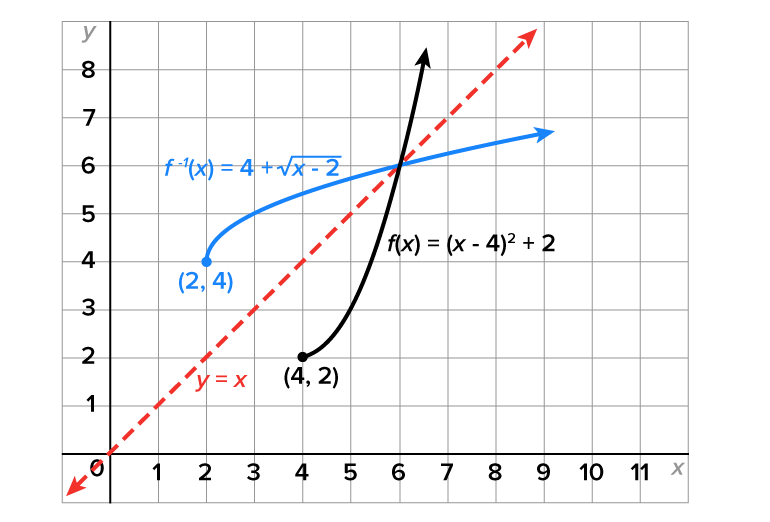
A graph with an x-axis ranging from 0 to 11 and a y-axis ranging from 0 to 8. The graph consists of a dashed slanted line labeled y equals x that extends from the point (0, 0) to a point beyond (8, 8). The graph also has two curves, where the first curve f of x equals (x minus 4) squared plus 2 opens upward from the marked point (4, 2), passes through the point (6, 6), and rises into the first quadrant. The second curve f inverse of x equals 4 plus square root of (x−2) opens downward from the marked point (2, 4), passes through the point (6, 6), and rises into the first quadrant. The dashed line and the two curves intersect at the point (6, 6).

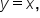As you can see, the graphs together are symmetric with respect to the line y equals x comma which confirms that they are inverses.

Here is another example that has a different domain restriction.

EXAMPLE

Consider the function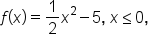 f open parentheses x close parentheses equals 1 half x squared minus 5 comma space x less or equal than 0 comma whose graph is shown below.

A graph with an x-axis ranging from −5 to 2 and a y-axis ranging from −5 to 4. The left half of a parabola with vertex (0, -5). The rightmost point is (0, -5), and the graph also passes through (-2, -3) and (-4, 3).

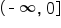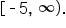
The domain was already given as open parentheses short dash infinity comma space 0 close square brackets and the range of f open parentheses x close parentheses is open square brackets short dash 5 comma space infinity close parentheses.

Now, let’s find its inverse function.

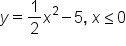
y equals 1 half x squared minus 5 comma space x less or equal than 0 Replace f open parentheses x close parentheses with y.
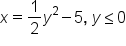
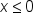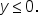
x equals 1 half y squared minus 5 comma space y less or equal than 0 Interchange x and y. Since x and y are interchanged, x less or equal than 0 becomes y less or equal than 0.
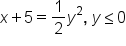
x plus 5 equals 1 half y squared comma space y less or equal than 0 Add 5 to both sides.
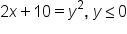
2 x plus 10 equals y squared comma space y less or equal than 0 Multiply both sides by 2 and distribute.
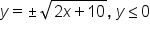
y equals plus-or-minus square root of 2 x plus 10 end root comma space y less or equal than 0 Apply the square root principle.

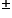Because of the “plus-or-minus", this is not a function. The domain and range of f open parentheses x close parentheses and its inverse are used to determine if the “+” or “-” is used.

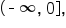Since the domain of f open parentheses x close parentheses is open parentheses short dash infinity comma space 0 close square brackets comma the range of the inverse is also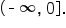 open parentheses short dash infinity comma space 0 close square brackets.

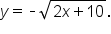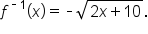
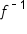Since a square root always returns a positive value, the negative version of the square root is the inverse. Thus, the inverse is y equals short dash square root of 2 x plus 10 end root. This can now be written using function notation, so we can formally say that the inverse is f to the power of short dash 1 end exponent open parentheses x close parentheses equals short dash square root of 2 x plus 10 end root.

The graphs of f and f to the power of short dash 1 end exponent are shown in the graph, along with the line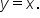 y equals x.

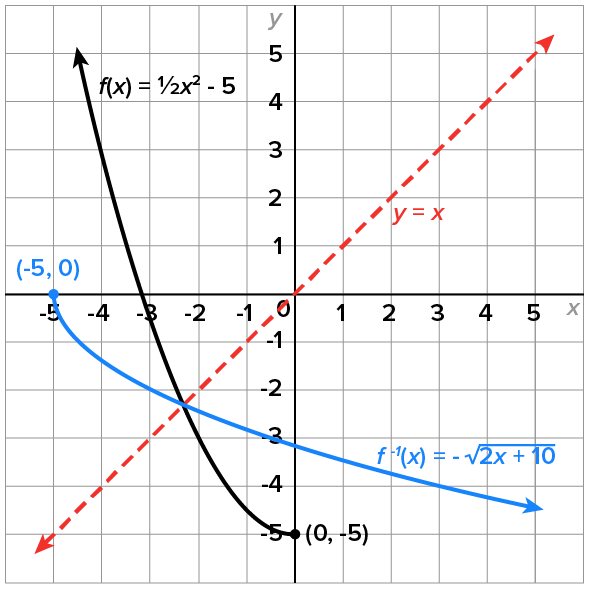
A graph with an x-axis and a y-axis ranging from −5 to 5. The graph consists of a dashed slanted line labeled y equals x that extends from the third quadrant to the first quadrant, passing through the point (0, 0). The graph also has two curves, where the first curve f of x equals one half x squared minus 5 opens upward from the marked point (0, −5) in the third quadrant, passes through the points (−2.4, −2.4) and (−3.2 0), and rises upward into the second quadrant. The second curve f inverse of x equals negative square root of (2x plus 10) opens rightward from the marked point (−5, 0), passes through the points (−2.4, −2.4) and (0, −3.2), and descends into the fourth quadrant. The dashed line and the two curves intersect at the point (−2.4, −2.4).

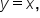As you can see, the graphs together are symmetric with respect to the line y equals x comma which confirms that they are inverses.

try it
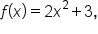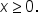
Consider the function f open parentheses x close parentheses equals 2 x squared plus 3 comma where x greater or equal than 0.
Find the inverse of f   (x  ).
Since the function is one-to-one on its domain, an inverse function exists.

Now to find the inverse function:

y equals 2 x squared plus 3 Replace f open parentheses x close parentheses with y.
x equals 2 y squared plus 3 Interchange x and y.
x minus 3 equals 2 y squared The goal now is to solve for y. To begin, subtract 3 from both sides.
fraction numerator x minus 3 over denominator 2 end fraction equals y squared Divide both sides by 2.
y equals square root of fraction numerator x minus 3 over denominator 2 end fraction end root Apply the square root to both sides to solve for y. Since the domain of f open parentheses x close parentheses is x greater or equal than 0 comma the range of the inverse is y greater or equal than 0. Therefore, we only consider the positive square root when solving for y.

Therefore, f to the power of short dash 1 end exponent open parentheses x close parentheses equals square root of fraction numerator x minus 3 over denominator 2 end fraction end root.

Now, let’s see how this works when f open parentheses x close parentheses is a square root function.

EXAMPLE

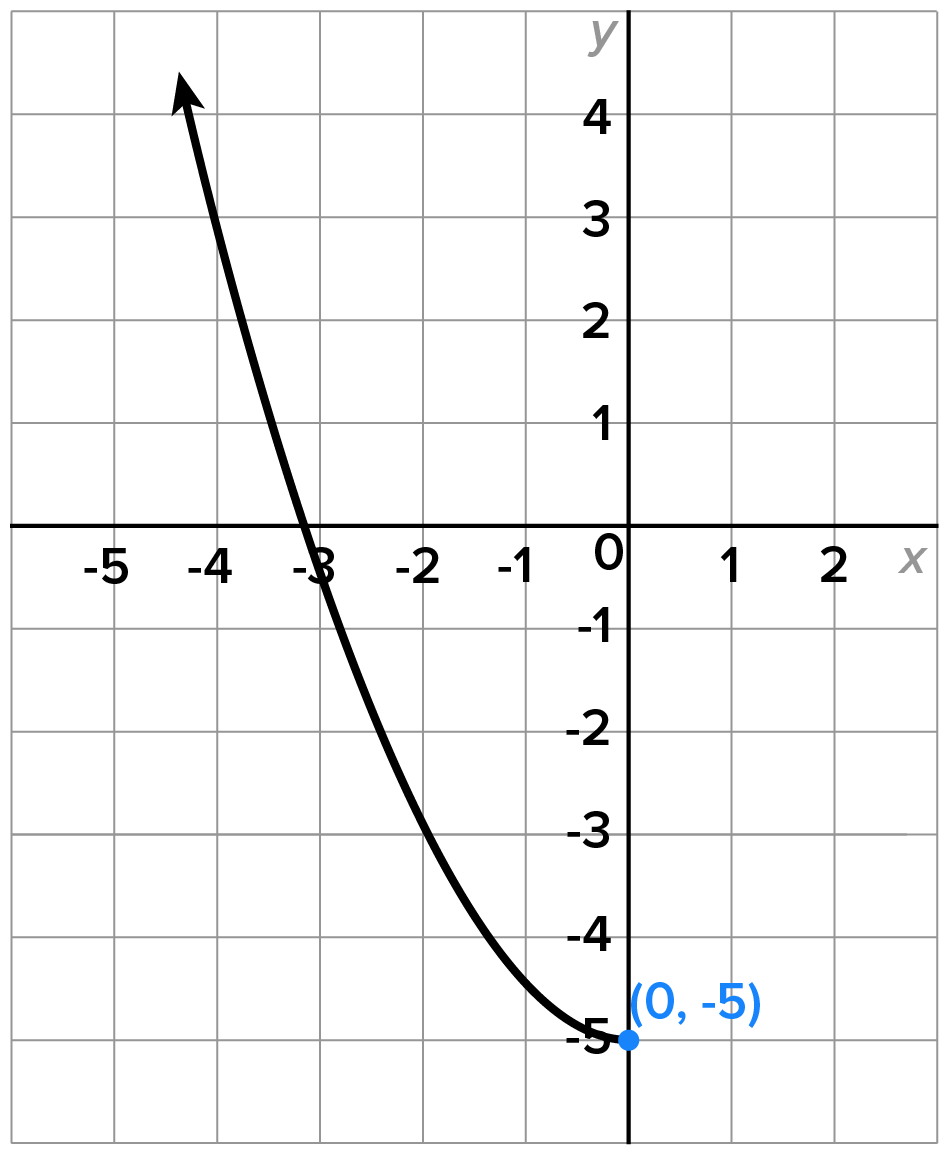
Consider the function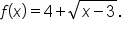 f open parentheses x close parentheses equals 4 plus square root of x minus 3 end root.

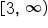If you graph the function, you will notice that f open parentheses x close parentheses has domain open square brackets 3 comma space infinity close parentheses and range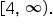 open square brackets 4 comma space infinity close parentheses.

Now, let’s find the inverse:

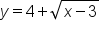
y equals 4 plus square root of x minus 3 end root Replace f open parentheses x close parentheses with y.
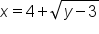
x equals 4 plus square root of y minus 3 end root Interchange x and y.
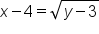
x minus 4 equals square root of y minus 3 end root Subtract 4 from both sides.
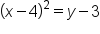
open parentheses x minus 4 close parentheses squared equals y minus 3 Square both sides.
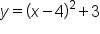
y equals open parentheses x minus 4 close parentheses squared plus 3 Add 3 to both sides; write y on the left-hand side.

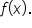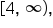This may seem like a final answer, but we have to be careful. We need to make sure that the domain of the inverse is the same as the range of f open parentheses x close parentheses. Since the range of f open parentheses x close parentheses is open square brackets 4 comma space infinity close parentheses comma this is also the domain of the inverse function.

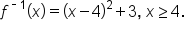
Conclusion: the inverse function is f to the power of short dash 1 end exponent open parentheses x close parentheses equals open parentheses x minus 4 close parentheses squared plus 3 comma space x greater or equal than 4.

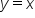The graphs of f and its inverse, along with the line y equals x, are shown in the figure.

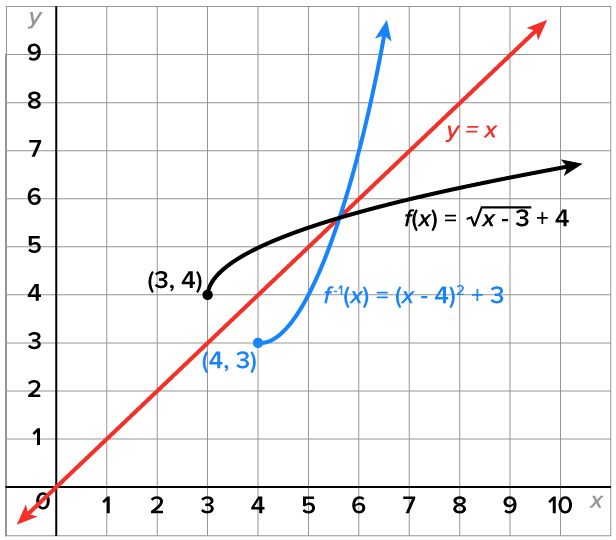
A graph with an x-axis ranging from 0 to 10 and a y-axis ranging from 0 to 9. The graph consists of a dashed slanted line labeled y equals x that passes through the points (0, 0) and extends beyond the point (9, 9). The graph also has two curves, where the first curve f inverse of x equals (x − 4) squared plus 3 opens upward from the marked point (4, 3) and passes through the point (5.5, 5.5) to rise upward into the first quadrant. The second curve f of x equals square root of (x minus 3) plus 4 opens downward from the marked point (3, 4) and passes through the point (5.5, 5.5) to gently rise into the first quadrant. The two curves and the dashed slanted line intersect at the point (5.5, 5.5).

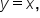As you can see, the graphs together are symmetric with respect to the line y equals x comma which confirms that they are inverses.

try it
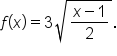
Consider the function f open parentheses x close parentheses equals 3     square root of fraction numerator x minus 1 over denominator 2 end fraction end root.
Find its inverse function.
Follow the usual process to find the inverse:

y equals 3     square root of fraction numerator x minus 1 over denominator 2 end fraction end root Replace f open parentheses x close parentheses with y.
x equals 3     square root of fraction numerator y minus 1 over denominator 2 end fraction end root Interchange x and y.
x over 3 equals square root of fraction numerator y minus 1 over denominator 2 end fraction end root The goal now is to solve for y. To begin, divide both sides by 3.
open parentheses x over 3 close parentheses squared equals fraction numerator y minus 1 over denominator 2 end fraction Square both sides.
x squared over 9 equals fraction numerator y minus 1 over denominator 2 end fraction Simplify the left-hand side.
fraction numerator 2 x squared over denominator 9 end fraction equals y minus 1 Multiply both sides by 2.
fraction numerator 2 x squared over denominator 9 end fraction plus 1 equals y Add 1 to both sides. We have now solved for y.

Since this is a quadratic function, it is important to restrict the domain since quadratic functions are not generally one-to-one.

Looking at the original function, the range of f open parentheses x close parentheses is y greater or equal than 0 comma since f open parentheses x close parentheses is a square root function.

Thus, the domain of f to the power of short dash 1 end exponent open parentheses x close parentheses is x greater or equal than 0 comma since the range of f open parentheses x close parentheses is the same set of numbers as the domain of f to the power of short dash 1 end exponent open parentheses x close parentheses.

Thus, f to the power of short dash 1 end exponent open parentheses x close parentheses equals 2 over 9 x squared plus 1 comma space x greater or equal than 0.

At this point, it’s clear to see that the inverse of a quadratic function is a square root function, and vice versa. This can be extended to polynomial functions and their inverses, when inverses exist.

2b. Inverses of Other Polynomial Functions

Not all polynomial functions have inverse functions.

For example, consider the function 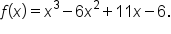f open parentheses x close parentheses equals x cubed minus 6 x squared plus 11 x minus 6. If you graph the function, you will see that it is not one-to-one, and therefore doesn’t have an inverse function.

Even when a polynomial function is one-to-one, finding its inverse could prove to be difficult.

EXAMPLE

Consider the function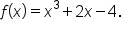 f open parentheses x close parentheses equals x cubed plus 2 x minus 4.

By graphing the function, you see this is one-to-one. However, when we try to find the inverse, we run into trouble:

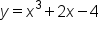
y equals x cubed plus 2 x minus 4 Replace f open parentheses x close parentheses with y.
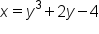
x equals y cubed plus 2 y minus 4 Interchange x and y.

Once we get to this point, there is no straightforward way to solve for y. We know the inverse exists, but getting an expression for the inverse is beyond the scope of this course.

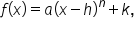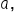That said, polynomial functions of the form f open parentheses x close parentheses equals a open parentheses x minus h close parentheses to the power of n plus k comma where a comma h, and k are numbers and n is a positive integer, can be inverted quite easily. When n is even, the domain needs to be restricted; and when n is odd, the inverse is valid for all real numbers.

Here is an example, similar to those we did earlier in the course.

EXAMPLE

Consider the function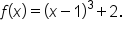 f open parentheses x close parentheses equals open parentheses x minus 1 close parentheses cubed plus 2. The domain and range of f open parentheses x close parentheses are the set of real numbers.

The function is one-to-one. Therefore, we can find its inverse.

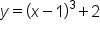
y equals open parentheses x minus 1 close parentheses cubed plus 2 Replace f open parentheses x close parentheses with y.
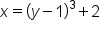
x equals open parentheses y minus 1 close parentheses cubed plus 2 Interchange x and y.
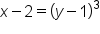
x minus 2 equals open parentheses y minus 1 close parentheses cubed Subtract 2 from both sides.
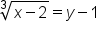
cube root of x minus 2 end root equals y minus 1 Apply the cube root to both sides.
Note: “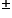plus-or-minus” is not used with odd roots.
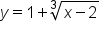
y equals 1 plus cube root of x minus 2 end root Add 1 to both sides; write y on the left-hand side.

The domain and range of the inverse function are the set of real numbers.

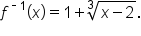Thus, f to the power of short dash 1 end exponent open parentheses x close parentheses equals 1 plus cube root of x minus 2 end root. If you graph both f and its inverse function on the same axes, you will observe symmetry over the line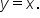 y equals x.

watch
Check out this video to see an example of finding the inverse function of a function with an even index.

try it
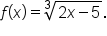
Consider the function f open parentheses x close parentheses equals cube root of 2 x minus 5 end root.
Find its inverse function.
Follow the usual process to find the inverse function. Note that the domain and range of f open parentheses x close parentheses are both the set of all real numbers, so there will be no domain restriction for the inverse.

y equals cube root of 2 x minus 5 end root Replace f open parentheses x close parentheses with y.
x equals cube root of 2 y minus 5 end root Interchange x and y.
x cubed equals 2 y minus 5 The goal now is to solve for y. Start by cubing both sides.
x cubed plus 5 equals 2 y Add 5 to both sides.
y equals fraction numerator x cubed plus 5 over denominator 2 end fraction Divide both sides by 2. We have now solved for y.

Thus, f to the power of short dash 1 end exponent open parentheses x close parentheses equals fraction numerator x cubed plus 5 over denominator 2 end fraction.

As you can see through these last two examples, the inverse of a cubic function is a cube root function, and vice versa. In general, the inverse of a polynomial function of degree n is an nth root function.

This next example shows us why we need to use inverses.

EXAMPLE

A sphere of radius r has volume V open parentheses r close parentheses equals 4 over 3 straight pi r cubed.

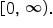
Since r and V are both measurements, the domain and range of this function are both open square brackets 0 comma space infinity close parentheses.

This function gives the volume of a sphere with a given radius. This means that the inverse function will give the radius for a given volume.

So we don’t lose the context of r and V in this problem, we will simply solve for r and not interchange the variables to find the inverse function.

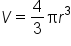
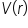V equals 4 over 3 straight pi r cubed Replace V open parentheses r close parentheses with V.
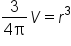
fraction numerator 3 over denominator 4 straight pi end fraction V equals r cubed Multiply both sides by 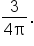fraction numerator 3 over denominator 4 straight pi end fraction.
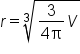
r equals cube root of fraction numerator 3 over denominator 4 straight pi end fraction V end root Take the cube root of both sides, and write r on the left-hand side.

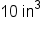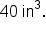Now let’s suppose that you are designing spherical shapes and you know the volume of the shapes are to be 10 space in cubed and 40 space in cubed. This formula can easily be used to estimate the radius of each sphere.

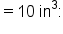
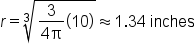
Volume equals 10 space in cubed colon r equals cube root of fraction numerator 3 over denominator 4 straight pi end fraction open parentheses 10 close parentheses end root almost equal to 1.34 space inches
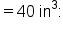
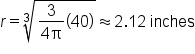
Volume equals 40 space in cubed colon r equals cube root of fraction numerator 3 over denominator 4 straight pi end fraction open parentheses 40 close parentheses end root almost equal to 2.12 space inches

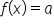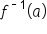In general, inverse functions are useful as an alternative to solving f open parentheses x close parentheses equals a for some value of a. When f open parentheses x close parentheses has an inverse function, we can evaluate f to the power of short dash 1 end exponent open parentheses a close parentheses instead.

summary
In this lesson, we limited our scope to polynomial and radical functions and their inverses. You learned that when a function is not one-to-one, restricting the domain of the function so that it is one-to-one is necessary to find the inverse of the new function. Typically, the largest possible domain is chosen. You also learned how to find the inverse of polynomial and radical functions, understanding that the inverse of a quadratic function is a square root function, and vice versa; in general, the inverse of a polynomial function of degree n is an nth root function. Inverses are used to solve application problems as an alternative to solving f open parentheses x close parentheses equals a.

SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.