Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Residuals

Author: Sophia

what's covered
This tutorial will cover the topic of residuals, which occur when you fit a line to data points. Our discussion breaks down as follows:

Table of Contents

1. Residuals

When you create a best-fit line, typically it doesn't pass through all the points. The only way it would pass through all the points is if the correlation was exactly 1, which means that all the points lie exactly on a line.

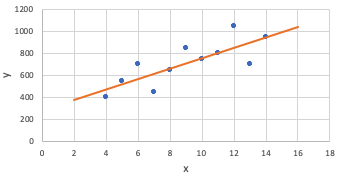
A scatterplot with an x-axis ranging from 0 to 18 at intervals of 2 and a y-axis ranging from 0 to 1,200 at intervals of 200. Several data points are scattered across the graph, forming an overall upward pattern. A line of best fit slopes upward from left to right. Most data points lie close to the line; a few deviate slightly above or below it.

Most of the time, they don't lie exactly on a line. In that case, most of the points are going to have some difference between what the line predicts and the value that they actually are. Because the line shows predictions, they'll be off a little bit from the actual values, even if only by a little.

A residual is the amount by which the predictions are off from the actual amount.

EXAMPLE

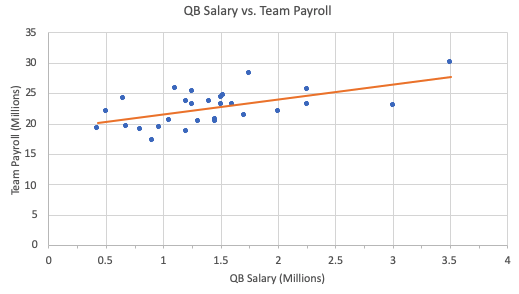
The scatterplot below shows the 1992 payrolls for the National Football League for their quarterback, who's usually their most expensive player, and for the entire team.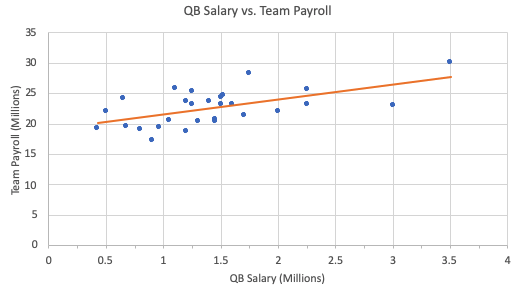
A scatterplot titled ‘QB Salary vs. Team Payroll’. The x-axis is labeled ‘QB Salary’, with values in millions ranging from 0 to 4 at intervals of 0.5 million, and the y-axis is labeled ‘Team Payroll’, with values in millions ranging from 0 to 35 at intervals of 5 million. Several data points are scattered mostly between 0.5 and 2.5 along the x-axis and 18 and 28 along the y-axis. Several data points deviate somewhat around a generally upward-sloping best-fit line from (0.4, 20) to (3.5, 28).
The best-fit line shows the predicted payrolls of a team if the quarterback makes a certain amount of money. The predicted payroll (payroll-hat) is equal to $18.8 million plus three times the quarterback salary (QB). The equation of this line is:

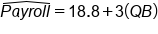
stack P a y r o l l with hat on top equals 18.8 plus 3 left parenthesis Q B right parenthesis

Let's consider the Dallas Cowboys, circled in the scatterplot.
A scatterplot titled ‘QB Salary vs. Team Payroll’. The x-axis is labeled ‘QB Salary’, with values in millions ranging from 0 to 4 at intervals of 0.5 million, and the y-axis is labeled ‘Team Payroll’, with values in millions ranging from 0 to 35 at intervals of 5 million. Several data points are scattered mostly between 0.5 and 2.5 along the x-axis and 18 and 28 along the y-axis. Several data points deviate somewhat around a generally upward-sloping best-fit line from (0.4, 20) to (3.5, 28). A data point at approximately (1.75, 29) is encircled.
They pay their quarterback $1.75 million, and they pay the overall team $28.394 million, which is well above what the line would predict for a team that pays their quarterback that amount of money. To find the predictive value, we can use the best-fit line equation, plug in the value of the quarterback salary for the Cowboys, and solve for the team payroll.

table attributes columnalign left end attributes row cell stack P a y r o l l with hat on top equals 18.8 plus 3 left parenthesis Q B right parenthesis end cell row cell stack P a y r o l l with hat on top equals 18.8 plus 3 left parenthesis 1.75 right parenthesis end cell row cell stack P a y r o l l with hat on top equals 18.8 plus 5.25 end cell row cell stack P a y r o l l with hat on top equals 24.05 end cell end table

We would predict that if a team pays their quarterback $1.75 million, their team payroll would be $24.05 million. We can also look at this visually to confirm this predictive value.
A scatterplot titled ‘QB Salary vs. Team Payroll’. The x-axis is labeled ‘QB Salary’, with values in millions ranging from 0 to 4 at intervals of 0.5 million, and the y-axis is labeled ‘Team Payroll’, with values in millions ranging from 0 to 35 at intervals of 5 million. Several data points are scattered mostly between 0.5 and 2.5 along the x-axis and 18 and 28 along the y-axis. Several data points deviate somewhat around a generally upward-sloping best-fit line from (0.4, 20) to (3.5, 28). A data point at approximately (1.75, 29) is encircled. A dashed horizontal line extends from (0, 24) to (1.75, 24) on the upward-sloping line and then bends vertically downward to meet the x-axis at (1.75, 0).
However, when you look at the Dallas Cowboys' data, the actual payroll is $28.394 million. That's over $4 million more than the line would have predicted their payroll to be. This vertical distance between the $28.394 million that is actually being paid versus the $24.05 million that's being predicted is called the residual between those two values.
A scatterplot titled ‘QB Salary vs. Team Payroll’. The x-axis is labeled ‘QB Salary’, with values in millions ranging from 0 to 4 at intervals of 0.5 million, and the y-axis is labeled ‘Team Payroll’, with values in millions ranging from 0 to 35 at intervals of 5 million. Several data points are scattered mostly between 0.5 and 2.5 along the x-axis and 18 and 28 along the y-axis. Several data points deviate somewhat around a generally upward-sloping best-fit line from (0.4, 20) to (3.5, 28). A data point at approximately (1.75, 29) is encircled, and a vertical line from this point extends downward to meet the best-fit line.
The residual is calculated by taking the actual response value, y, minus the predicted response value, y-hat.

formula to know
Residual
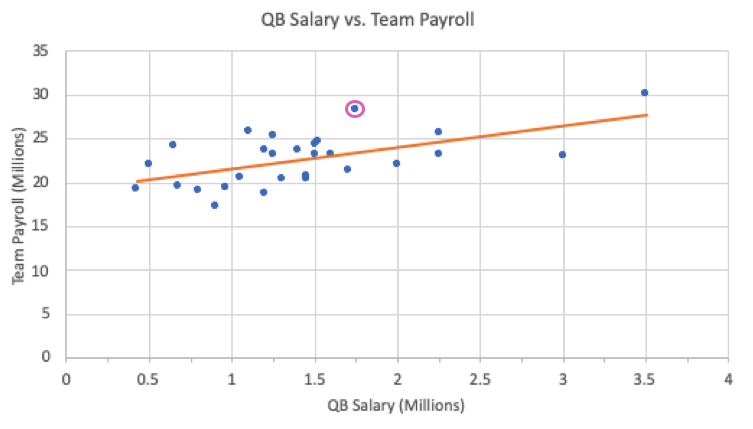
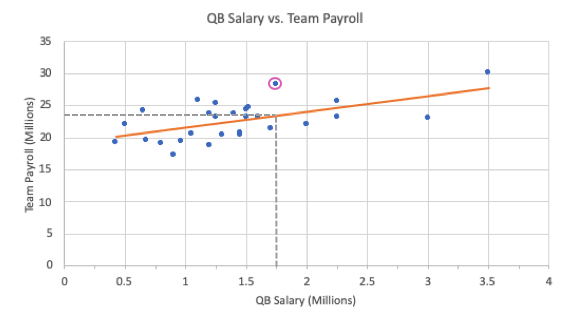
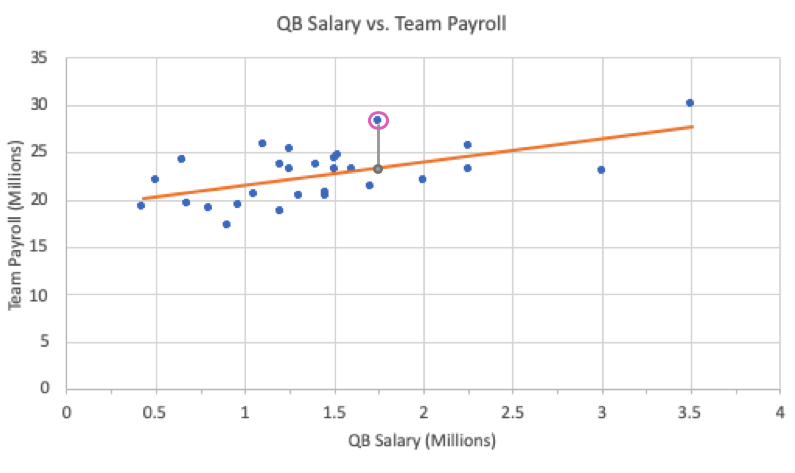
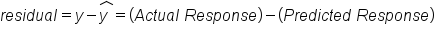
r e s i d u a l equals y minus stack y space with hat on top equals left parenthesis A c t u a l space R e s p o n s e right parenthesis minus left parenthesis P r e d i c t e d space R e s p o n s e right parenthesis

In the payroll example outlined above, the residual for the Dallas Cowboys is calculated by taking the actual team payroll minus the predicted team payroll:

table attributes columnalign left end attributes row cell R e s i d u a l equals a c t u a l space r e s p o n s e minus p r e d i c t e d space r e s p o n s e end cell row cell R e s i d u a l equals 28.394 minus 24.05 end cell row cell R e s i d u a l equals 4.344 end cell end table

In this particular problem, the residual for the Dallas Cowboys ends up being $4.344 million. This is a positive number.

Every point has a residual value:

  • If the actual response falls above the best-fit line, meaning the actual response is higher than the predicted response, the residual value is positive.
  • If the actual response falls below the best-fit line, meaning the actual response is lower than the predicted response, the residual value is negative.
  • If by some chance the point falls on the line, the residual value is zero.
term to know
Residual
The difference between the actual value of the response variable for a particular data point and its predicted value from the regression line.

2. Residual Plots

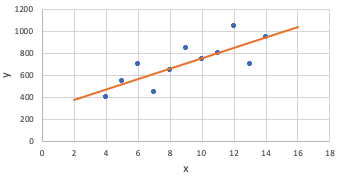
Since every point has a residual value, you can actually plot the explanatory variable vs. the residual value, as opposed to the explanatory variable vs. the response variable.

Scatterplot

Explanatory
vs.
Response 		A scatterplot with an x-axis ranging from 0 to 18 at intervals of 2 and a y-axis ranging from 0 to 1,200 at intervals of 200. Several data points are scattered across the graph, forming an overall upward pattern. A line of best fit slopes upward from left to right. Most data points lie close to the line; a few deviate slightly above or below it.
Residual Plot

Explanatory
vs.
Residual

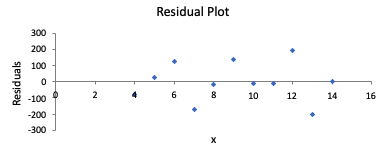
The second graph, where you see how far off the predictions are, is called a residual plot. A residual plot is quite useful because it can help you evaluate whether or not a line is actually a useful predictor for the data.

A good linear model will have:

  • Points above and below the line in random scatters
  • No curved pattern in the residuals
  • Equal variability throughout the entire residual plot
Good Example of Linear Model
A scatterplot titled ‘QB Salary vs. Team Payroll’. The x-axis is labeled ‘QB Salary’, with values in millions ranging from 0 to 4 at intervals of 0.5 million, and the y-axis is labeled ‘Team Payroll’, with values in millions ranging from 0 to 35 at intervals of 5 million. Several data points are scattered mostly between 0.5 and 2.5 along the x-axis and 18 and 28 along the y-axis. Several data points deviate somewhat around a generally upward-sloping best-fit line from (0.4, 20) to (3.5, 28).

A residual plot has an x-axis labeled ‘QB Salary, in millions’, ranging from 0 to 4 at intervals of 0.5 million, and a y-axis labeled ‘Residuals’, ranging from about −4 to 6 at intervals of 2. Data points are scattered above and below the horizontal axis and between −4 and 6 on the y-axis, with no clear pattern. Most points cluster between 0.5 and 2.5 on the x-axis and −3 and 5 on the y-axis.
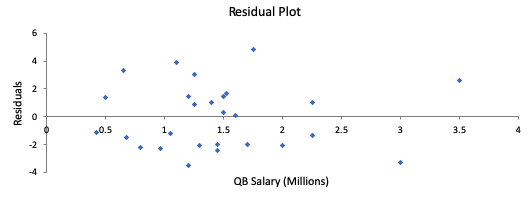
This is a good choice for a best-fit line.

The points above and below the line are in random scatters, there is no curved pattern in the residual plot, and there is equal variability throughout the entire residual plot.
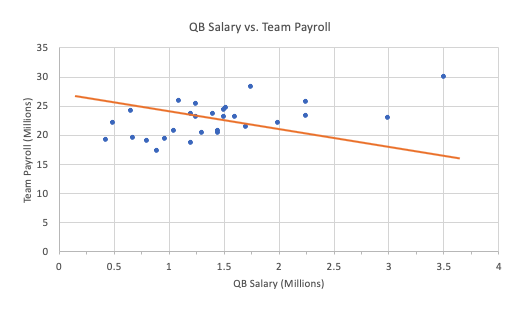
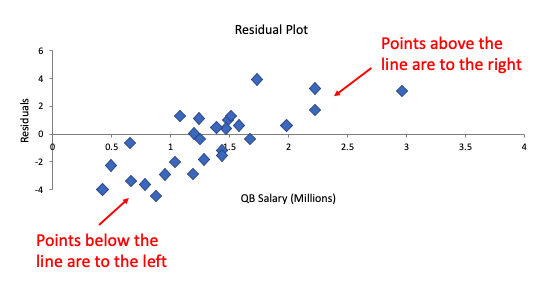
Bad Example: Does Not Have Random Scatter
A scatterplot titled ‘QB Salary vs. Team Payroll’ with the x-axis labeled ‘QB Salary (Millions)’, ranging from 0 to 4 at intervals of 0.5 million, and the y-axis labeled ‘Team Payroll (Millions)’, ranging from 0 to 35 at intervals of 5 million. Most data points are clustered between 0.5 and 2.5 on the x-axis and between 18 and 28 on the y-axis, forming an overall upward pattern. An orange best-fit line slopes downward from left to right, beginning near y equals 26 at x equals 0.2 and ending near y equals 16 at x equals 3.6.

A residual plot titled 'Residual Plot' with the x-axis labeled 'QB Salary (Millions)' ranging from 0 to 4 at intervals of 0.5 and the y-axis labeled 'Residuals' ranging from about −4 to 6 at intervals of 2. Data points are plotted above and below the horizontal axis. Most points on the left side of the graph, between approximately x equals 0.5 and x equals 1.5, have negative residuals below zero. Most points on the right side of the graph, between approximately x equals 2 and x equals 3.5, have positive residuals above zero. Red annotation text with arrows labels the lower-left cluster 'Points below the line are to the left' and the upper-right cluster 'Points above the line are to the right.'
This is a bad choice for a best-fit line.

Although it has points above and below as residuals, it is not randomly scattered like the original one was. There is a clear pattern that is shown on the residual. This one has points that are below only on the left, and points that are above only on the right. That's what makes this line a poor choice for a line of best fit.
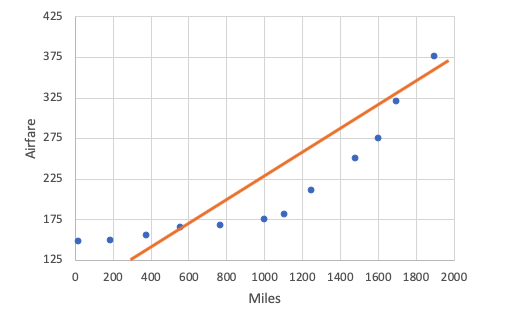
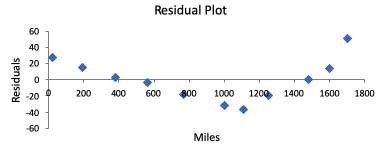
Bad Example: Has a Curved Pattern in Residual
A scatterplot with the x-axis labeled 'Miles' ranging from 0 to 2,000 at intervals of 200 and the y-axis labeled 'Airfare' ranging from 125 to 425 at intervals of 50. An upward-sloping best-fit line extends from approximately (300, 125) to (1,950, 370). Data points show an overall upward trend, with points at lower mile values around 0 to 600 and higher mile values around 1,600 to 1,900 tending to fall above the line, while many points in the middle range between approximately 900 and 1,500 miles fall below the line. The plotted points include approximate values such as (0, 150), (200, 150), (400, 160), (550, 170), (1,000, 175), (1,200, 185), (1,350, 210), (1,500, 250), (1,600, 275), (1,700, 320), and (1,900, 375).

A residual plot with an x-axis labeled ‘Miles’, ranging from about 0 to 1,800 at intervals of 200, and a y-axis labeled ‘Residuals’, ranging from about −60 to 60 at intervals of 20. Data points are scattered above and below the horizontal x-axis. A few residuals are positive at lower x-values, a few remain below the x-axis between (700, 0) and (1,300, 0), and a few data points are at higher x-values above the x-axis, from (1,400, 0) to (1,800, 0), creating a curved pattern.
This is a bad choice for a best-fit line.

Actually, a line doesn't make sense to predict this at all. You can verify that from the residual plot. What you see is a curved pattern in the residual plot. Also, it means that the scatter is not very random. What a curved pattern in the residual plot implies is that there is a better fit than a line for your data.
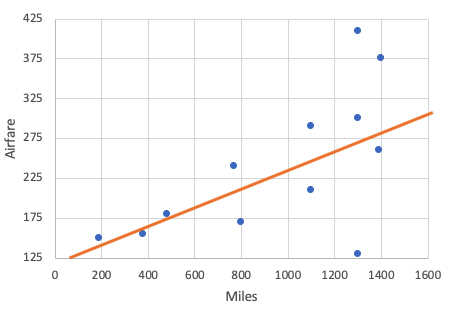
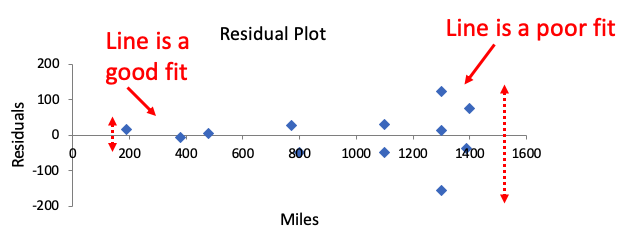
Bad Example: Unequal Variability
A scatterplot with the x-axis labeled 'Miles' ranging from 0 to 1,600 at intervals of 200 and the y-axis labeled 'Airfare' ranging from 125 to 425 at intervals of 50. Data points display an overall upward trend, and an upward-sloping best-fit line runs from approximately (50, 125) to (1,600, 300). Points at lower mile values are clustered close to the line, while points at higher mile values are spread farther above and below the line. Example plotted points include approximately (100, 150), (400, 155), (700, 240), (1,100, 290), (1,300, 410), and (1,400, 375).

A residual plot with the x-axis labeled ‘Miles’, ranging from 0 to 1,600 at intervals of 200, and the y-axis labeled ‘Residuals’, ranging from −200 to 200 at intervals of 100. Data points are scattered above and below a horizontal x-axis. The residuals are close to the x-axis on the left side of the plot, with small vertical deviations, indicating a good fit. On the right side, points are more widely spread above and below the line, with larger vertical distances, indicating a poor fit. On the right side, around 1,400 on the x-axis, the residuals are more widely spread above and below the line. The left-side data points are labeled ‘Line is a good fit’ with an arrow, and the right-side data points are labeled ‘Line is a poor fit’ with an arrow.
This is a bad choice for a best-fit line.

This residual plot shows sort of a trumpet pattern where the variability gets wider. The line is a good fit at the beginning because the residuals are small, but it's a poor fit at the end, where the residuals are getting larger. You can also see this in the scatterplot. They're close to the line; some are fitting the line well, and others are not fitting the line.

term to know
Residual Plot
A scatter plot that plots residuals vs. explanatory variable, as opposed to response variable vs. explanatory variable. It can be used to assess the fit of a line.

summary
Residuals are how much the data points are different than the line of best fit. They're positive if a point lies above the line, negative if it falls below the line, and zero if it falls on the line. You can use the resulting residual plot to determine if a line is actually an effective model for predicting the data.

Good luck!

Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.

Terms to Know
Residual

The difference between the actual value of the response variable for a particular data point and its predicted value from the regression line.

Residual Plot

A scatter plot that plots residuals vs. explanatory variable, as opposed to response variable vs. explanatory variable. It can be used to assess the fit of a line.

Formulas to Know
Residual

r e s i d u a l space equals space y space minus space y with overbrace on top space equals space left parenthesis A c t u a l space R e s p o n s e right parenthesis thin space minus space left parenthesis P r e d i c t e d space R e s p o n s e right parenthesis

© 2026 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.