Table of Contents |
The relative frequency probability method, also called the empirical method, is based on past experience. Let's explore a coin flip experiment to explain further.
Here is a chart for coin flips. You begin where it says "START."
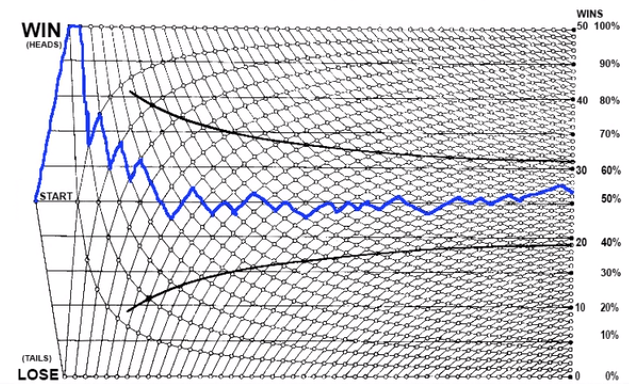
If you flip heads—for this scenario, heads will be defined as a win—you will go up the blue line that extends up to 100%. If you flip heads on the first trial, your experimental probability is 100%. If you flip heads on the next trial, it remains 100%. Next, if you flip a tail, then it reduces down to 66.6%. The graph simulates what would happen with the continuous flipping of coins.
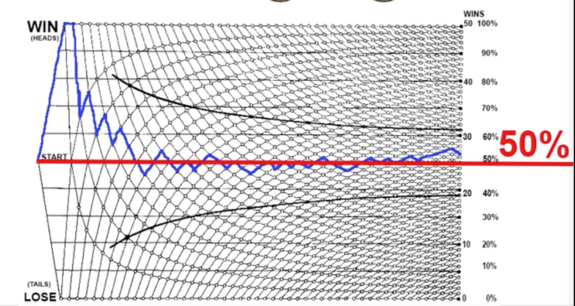
What do you notice? The graph is fairly erratic at the beginning, but it begins to settle down towards the end. It settles in right around 50%.
The relative frequency approach states that the probability of an event is the number of times it has occurred in identical trials, divided by the total number of trials. The relative frequency probability model is also called the empirical method, or experimental probability.
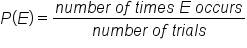
In the case of the coin flips, the chart indicates the probability of a coin coming up heads is 50%—not because there are two faces to the coin, but rather because heads have come up about half the time in repeated trials of coin flipping.
One additional way to talk about probability is called the subjective probability approach. It's not a mathematical model like some of the others that we discussed, like the frequentist approach or the a priori model, but it's based on your judgment.
You might hear words like this all the time:
"I'm 90% certain I left the garage open."
Does that mean that if the frequentist approach was used, you would say, "Ninety percent of the times that I felt this way, I did, in fact, leave the garage open"? It doesn't really make a lot of sense. You would basically be saying that you're more sure than not sure that you left the garage open.
What about this kind of a statement?
"I'd say there's about a 50-50 chance I got the job."
Again, what does that mean? About half the time you felt this way, you ended up getting the job? This isn't a frequentist approach. This isn't any mathematical model.
Or what about this?
"There's a one in a million chance of surviving that kind of accident."
Again, they're just saying that they don't think that this scenario is very possible or very probable. They're not saying that there have been a million such accidents and only one person survived.
Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.