Table of Contents |
Although we are used to measuring angles with degrees, with 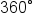 representing a full rotation around a circle, and as a result
representing a full rotation around a circle, and as a result 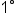 representing
representing 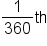 of one full rotation, this choice is arbitrary and is not related to anything tangible. In other words, by this standard, angles could be measured to represent any fraction of a full rotation (hundredths, twentieths, twelfths, etc.).
of one full rotation, this choice is arbitrary and is not related to anything tangible. In other words, by this standard, angles could be measured to represent any fraction of a full rotation (hundredths, twentieths, twelfths, etc.).
Consider a circle whose radius is r, centered at the origin.
The angle 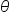 with vertex at center is selected so that the length of the circular arc intercepted by the angle is equal to the radius of the circle, as shown in the figure.
with vertex at center is selected so that the length of the circular arc intercepted by the angle is equal to the radius of the circle, as shown in the figure.
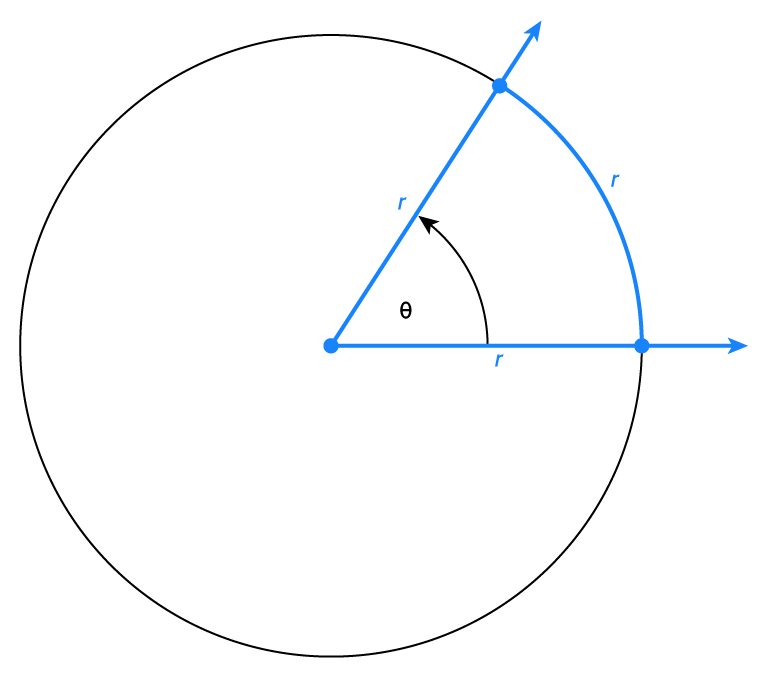
Since the angle has its vertex at the center of a circle, it is called a central angle. The measure of the angle in the figure is defined as 1 radian.
Now, consider an arc that has length s. Since each radian corresponds to a circular arc of length r, the quantity 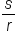 gives the measure of the central angle, measured in radians.
gives the measure of the central angle, measured in radians.
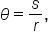 where s is the length of the arc and r is the radius of the circle that contains the arc.
where s is the length of the arc and r is the radius of the circle that contains the arc.Since 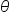 is the ratio of two lengths, its measure is unitless. It is not necessary (but is sometimes helpful) to write the label “radians” after an angle measure. If there is no degree symbol affixed to the angle measure, it is assumed that the angle is measured in radians.
is the ratio of two lengths, its measure is unitless. It is not necessary (but is sometimes helpful) to write the label “radians” after an angle measure. If there is no degree symbol affixed to the angle measure, it is assumed that the angle is measured in radians.
Now, let’s try to establish a relationship between degree measure and radian measure. Recall that the circumference of a circle is 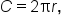 where r is the radius of the circle.
where r is the radius of the circle.
Consider the entire circumference of the circle, which is 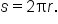 What angle in radians corresponds to a full rotation, meaning that the length of the circular arc is the circumference of the circle?
What angle in radians corresponds to a full rotation, meaning that the length of the circular arc is the circumference of the circle?
Since 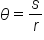 gives the central angle corresponding to a circular arc with length s, let
gives the central angle corresponding to a circular arc with length s, let 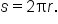
Then, 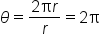 (since the radius is naturally not equal to 0).
(since the radius is naturally not equal to 0).
Thus, the central angle 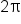 represents one full circular rotation. Recall that the angle
represents one full circular rotation. Recall that the angle 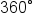 also represents one full circular rotation.
also represents one full circular rotation.
This means that 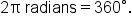 These angles are the same, but they are represented two different ways.
These angles are the same, but they are represented two different ways.
If we divide both sides of the equation by 2, we have 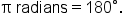 This equation is often easier to remember.
This equation is often easier to remember.
Now, we’ll use the equation  to establish formulas for 1 radian in terms of degrees and
to establish formulas for 1 radian in terms of degrees and 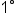 in terms of radians.
in terms of radians.
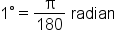
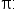
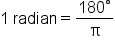
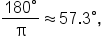 which means that 1 radian is approximately
which means that 1 radian is approximately 
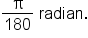
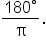
EXAMPLE
Convert the angle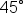 to radian measure, leaving the result in terms of
to radian measure, leaving the result in terms of 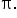
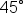 by
by 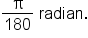
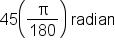
|
Multiply 45 by 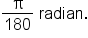
|
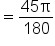
|
Perform the operation. |
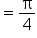
|
Reduce the fraction. |
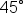 is equivalent to
is equivalent to 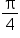 radian.
radian.
We will see throughout this course that some angles in radians are left as multiples of 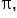 while some are approximated.
while some are approximated.
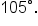
Now, we’ll convert from radian measure to degree measure.
EXAMPLE
Convert 1.2 radians to degree measure. Round to the nearest tenth of a degree.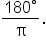
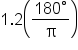
|
Multiply 1.2 by 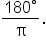
|
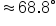
|
Use a calculator to approximate. |

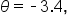 measured in radians.
measured in radians.
Using the formula 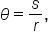 we can multiply both sides by r to obtain a formula that gives the length of the arc when the radius of the circle and the angle, measured in radians, are known.
we can multiply both sides by r to obtain a formula that gives the length of the arc when the radius of the circle and the angle, measured in radians, are known.
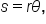 where r is the radius of the circle and
where r is the radius of the circle and 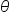 is the measure of the central angle, in radians.
is the measure of the central angle, in radians.EXAMPLE
The circular arc below has a central angle measuring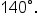 What is the exact length of the arc?
What is the exact length of the arc?
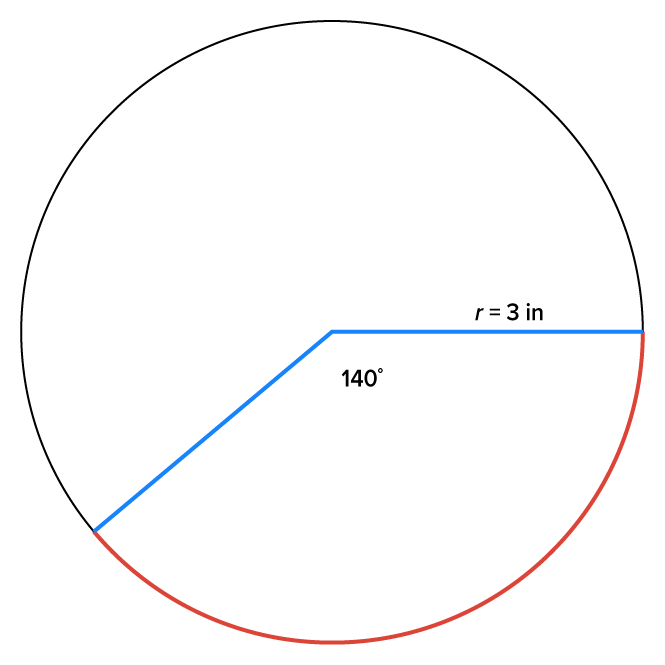
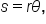 the angle
the angle 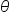 must be measured in radians.
must be measured in radians.
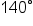 to radians.
to radians.
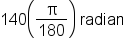
|
Multiply the angle by 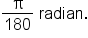
|
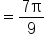
|
Multiply and reduce. |
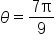 in the formula to find the length.
in the formula to find the length.
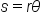
|
This is the formula for the length of the arc. |
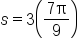
|
Substitute 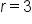 and and 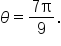
|
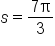
|
Simplify. |
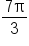 inches.
inches.
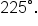
Have you ever played a CD and watched it spin and noticed how fast it goes? Depending on where the laser is reading the CD, it could spin anywhere between 200 and 500 revolutions per minute (rpm). This type of speed is an example of angular speed, a measure of how a rotation angle changes over time. The “revolutions” in rpm indicate that there is motion around a circle, as opposed to a straight line.
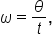 where
where 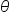 is the angle of rotation and t is the time elapsed.
is the angle of rotation and t is the time elapsed. 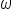 is the Greek letter omega.
is the Greek letter omega.Let’s start by solving some problems using angular speed.
EXAMPLE
A water wheel completes one full rotation every 5 seconds. What is its angular speed, measured in radians per second? Round your final answer to three decimal places.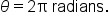
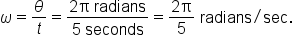
Sometimes we are given an angular speed in terms of revolutions per minute. Remember that each revolution means the angle rotated 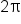 radians.
radians.
EXAMPLE
An old vinyl record turns at a rate of 45 revolutions per minute. What is its angular speed in radians per second?

|
Write the angular speed as a ratio. |
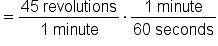
|
Since each minute has 60 seconds, multiply by a conversion factor. |

|
Since there are minutes in the numerator and denominator, they cancel. |

|
Simplify. |
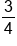 of a revolution every second. Since each revolution is
of a revolution every second. Since each revolution is 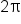 radians, the angular speed is
radians, the angular speed is 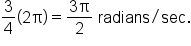
When you are traveling in a car at a rate of 60 miles per hour, this is an example of linear speed.
When traveling around a circle, the total distance traveled is the length of the circular arc, s. Since 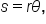 the distance traveled is affected by the angle of rotation as well as the radius of the circular path.
the distance traveled is affected by the angle of rotation as well as the radius of the circular path.
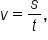 where s is the length of the arc (distance traveled) and t is the time interval.
where s is the length of the arc (distance traveled) and t is the time interval. 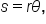
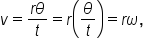 assuming that linear and angular speed are measured using the same units of time.
assuming that linear and angular speed are measured using the same units of time.EXAMPLE
A CD has a diameter of 12 centimeters. When playing audio, the angular speed varies to keep the linear speed constant where the disc is being read. When reading along the outer edge of the disc, the angular speed is about 400 revolutions per minute. What is its linear speed?
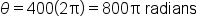
|
The CD is spinning at 400 revolutions per minute, and each revolution has a rotation angle of 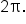
|
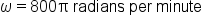
|
The rotation is happening at a rate of 400 revolutions per minute, which is 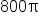 radians per minute. This is the angular speed in radians per minute. radians per minute. This is the angular speed in radians per minute.
|
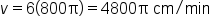
|
Use the formula 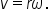
|
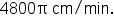
 to establish formulas for 1 radian in terms of degrees and
to establish formulas for 1 radian in terms of degrees and  in terms of radians, which then allowed you to convert between radian and degree measure. You also learned how to use radians to find the length of a circular arc and to solve problems with angular speed (a measure of how a rotation angle changes over time) and linear speed (the change in distance traveled per unit of time) for an object that is moving around a circular path.
in terms of radians, which then allowed you to convert between radian and degree measure. You also learned how to use radians to find the length of a circular arc and to solve problems with angular speed (a measure of how a rotation angle changes over time) and linear speed (the change in distance traveled per unit of time) for an object that is moving around a circular path.
SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS