Quantities in Chemical Reactions

1. The Mole

The identity of a substance is defined not only by the types of atoms or ions it contains but by the quantity of each type of atom or ion. In chemistry, the unit for the amount of a substance is the mole. The mole is an amount unit similar to familiar units like pair, dozen, gross, etc. It provides a specific measure of the number of atoms or molecules in a sample of matter. The mole provides a link between an easily measured macroscopic property—bulk mass—and an extremely important fundamental microscopic property—the number of atoms, molecules, and so forth.

term to know

Mole

A unit for the amount of a substance.

1a. Avogadro’s Number

A mole of a substance is that amount in which there are 6.02214076 × 10²³ discrete entities (atoms or molecules). This large number is a fundamental constant known as Avogadro's number (N_A) or the Avogadro constant in honor of Italian scientist Amedeo Avogadro. This constant is properly reported with an explicit unit of “per mole,” a conveniently rounded version being 6.022 × 10²³ molecules (or atoms)/mol.

Consistent with its definition as an amount unit, 1 mole of any element contains the same number of atoms as 1 mole of any other element. The masses of 1 mole of different elements, however, are different, since the masses of the individual atoms are drastically different. The molar mass of an element (or compound) is the mass in grams of 1 mole of that substance, a property expressed in units of grams per mole (g/mol).

In the image above, each sample contains 6.022 ×10²³ atoms —1.00 mol of atoms. From left to right (top row): 65.4 g zinc, 12.0 g carbon, 24.3 g magnesium, and 63.5 g copper. From left to right (bottom row): 32.1 g sulfur, 28.1 g silicon, 207 g lead, and 118.7 g tin.

The molar mass of any substance is numerically equivalent to its atomic or formula weight in amu. Per the amu definition, a single ¹²C atom weighs 12 amu (its atomic mass is 12 amu). A mole of ¹²C atoms weighs 12 g (its molar mass is 12 g/mol). This relationship holds for all elements, since their atomic masses are measured relative to that of the amu-reference substance, ¹²C. Extending this principle, the molar mass of a compound in grams is likewise numerically equivalent to its formula mass in amu.

In the image above, each sample contains 6.022 × 10²³ molecules or formula units—1.00 mol of the compound or element. Clockwise from the upper left: 130.2 g of C₈H₁₇OH (1-octanol, formula mass 130.2 amu), 454.4 g of HgI₂ (mercury(II) iodide, formula mass 454.4 amu), 32.0 g of CH₃OH (methanol, formula mass 32.0 amu) and 256.5 g of S₈ (sulfur, formula mass 256.5 amu).

While atomic mass and molar mass are numerically equivalent, keep in mind that they are vastly different in terms of scale, as represented by the vast difference in the magnitudes of their respective units (amu versus g).

think about it

To appreciate the enormity of the mole, consider a small drop of water weighing about 0.03 g. Although this represents just a tiny fraction of 1 mole of water (~18 g), it contains more water molecules than can be clearly imagined. If the molecules were distributed equally among the roughly seven billion people on earth, each person would receive more than 100 billion molecules.

terms to know

Avogadro's Number (N_A) (or Avogadro’s Constant)

The amount in which there are 6.02214076 × 10²³ discrete entities (atoms or molecules).

Molar Mass

The mass in grams of 1 mole of that substance, a property expressed in units of grams per mole (g/mol).

1b. Molar Mass

Being able to use the periodic table (see below) to calculate the molar mass of an atom or molecule is a vital skill needed to perform any of the calculations in this lesson. On the periodic table, the average atomic mass of each element is given in amu which is equivalent to g/mole. Therefore, sodium has an amu = 22.99, which is equivalent to 22.99 g/mol for the molar mass of sodium. Likewise, silicon would have a molar mass of 28.09 g/mol, and chlorine would have a molar mass of 35.45 g/mol.

IN CONTEXT

Recall that some elements form diatomic elements. Fluorine exists as F₂ and oxygen as O₂.

To calculate the molar mass of diatomic fluorine or oxygen, we need to multiply the molar mass by two. For example, the molar mass of fluorine (F₂) = 19.00 x 2 = 38 g/mol. The molar mass of oxygen (O₂) = 16.00 x 2 = 32 g/mol.

To calculate the molar mass of an element, you only need to go to the periodic table and look up the average atomic mass of the element, which is the molar mass (unless it is a diatomic and then you have to multiply the molar mass by two).

But to calculate the molar mass of a molecule, such as H₂O, you need to add up the molar masses of all the elements in the molecule. Water (H₂O) is composed of two atoms of H and 1 atom of O. Each H = 1.008 g/mol and each oxygen = 16.00 g/mol, so 2 H (2 x 1.008) plus one O (1 x 16.00) = 2.016 + 16.00 = 18.01 (using significant figure rules for adding). Therefore, the molar mass of water = 18.01 g/mol.

try it

What is the molar mass of glucose (C₆H₁₂O₆)?

Solution:

Glucose (C₆H₁₂O₆) is made of 6 atoms of carbon, 12 atoms of hydrogen, and 6 atoms of oxygen. To calculate the molar mass, you need to add up all the individual atoms molar mass to get the molecule’s molar mass:

6 atoms of carbon: 6 x 12.01 g/mol = 72.06 g/mol
12 atoms of hydrogen: 12 x 1.008 g/mol = 12.096 g/mol
6 atoms of oxygen: 6 x 16.00 g/mol = 96.00 g/mol

Molar mass of glucose (C₆H₁₂O₆) = 72.06 + 12.096 + 96.00 = 180.156

Using significant figures, the molar mass of glucose (C₆H₁₂O₆) = 180.16 g/mol.

Follow this link to WebElements to view an accessible version of the periodic table of elements.

2. Converting Between Moles, Grams, Molecules, and Atoms

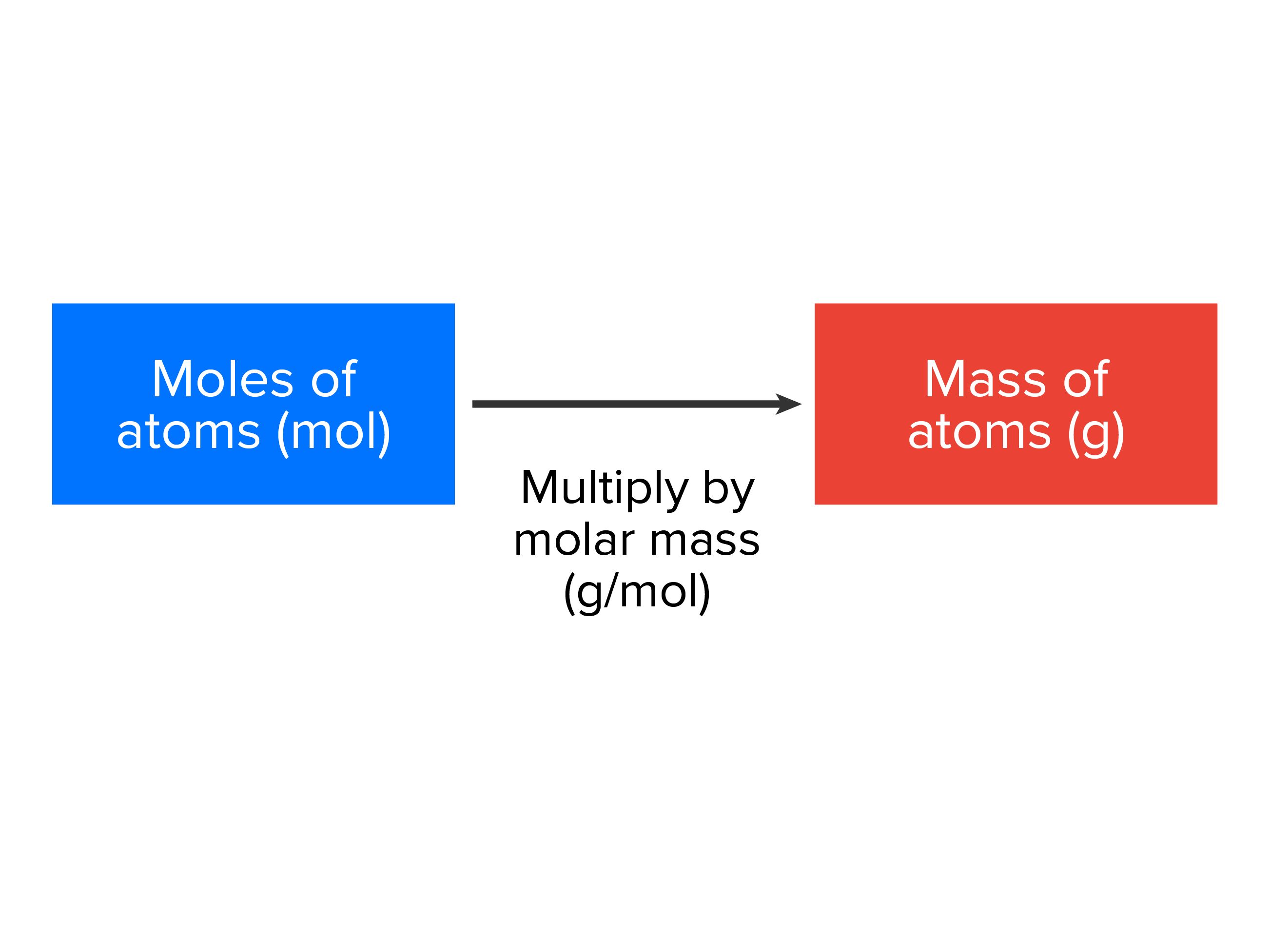
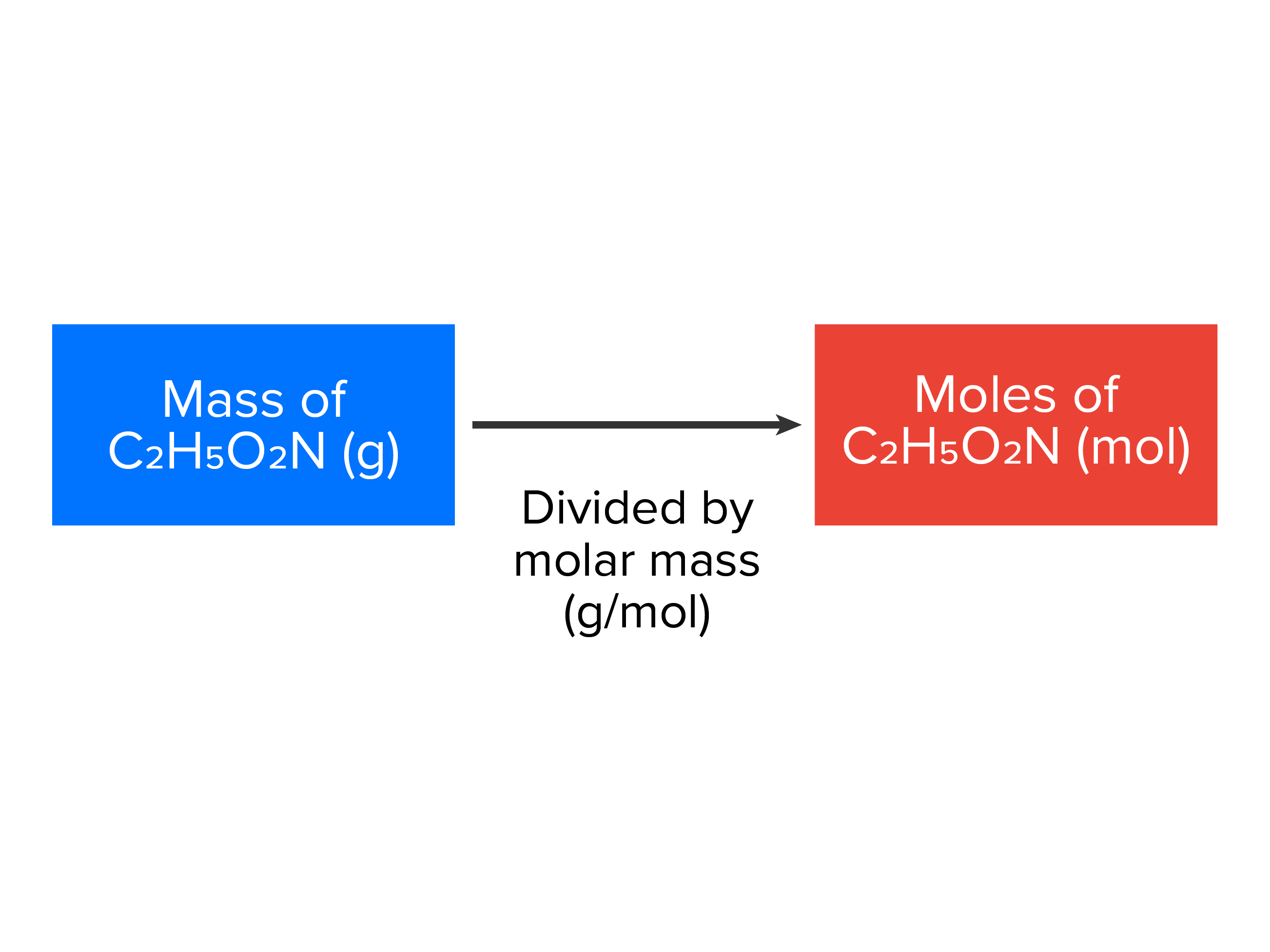
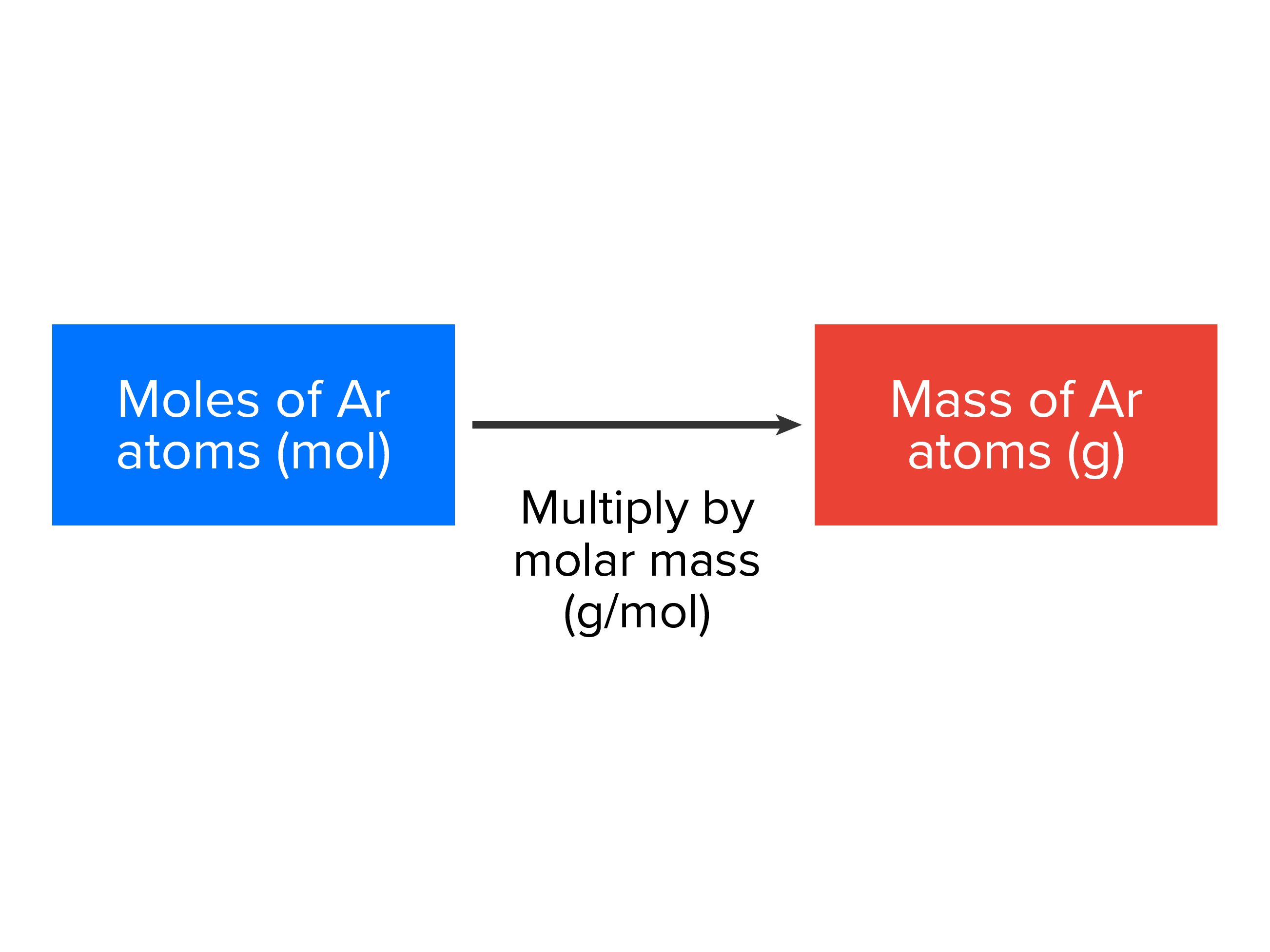
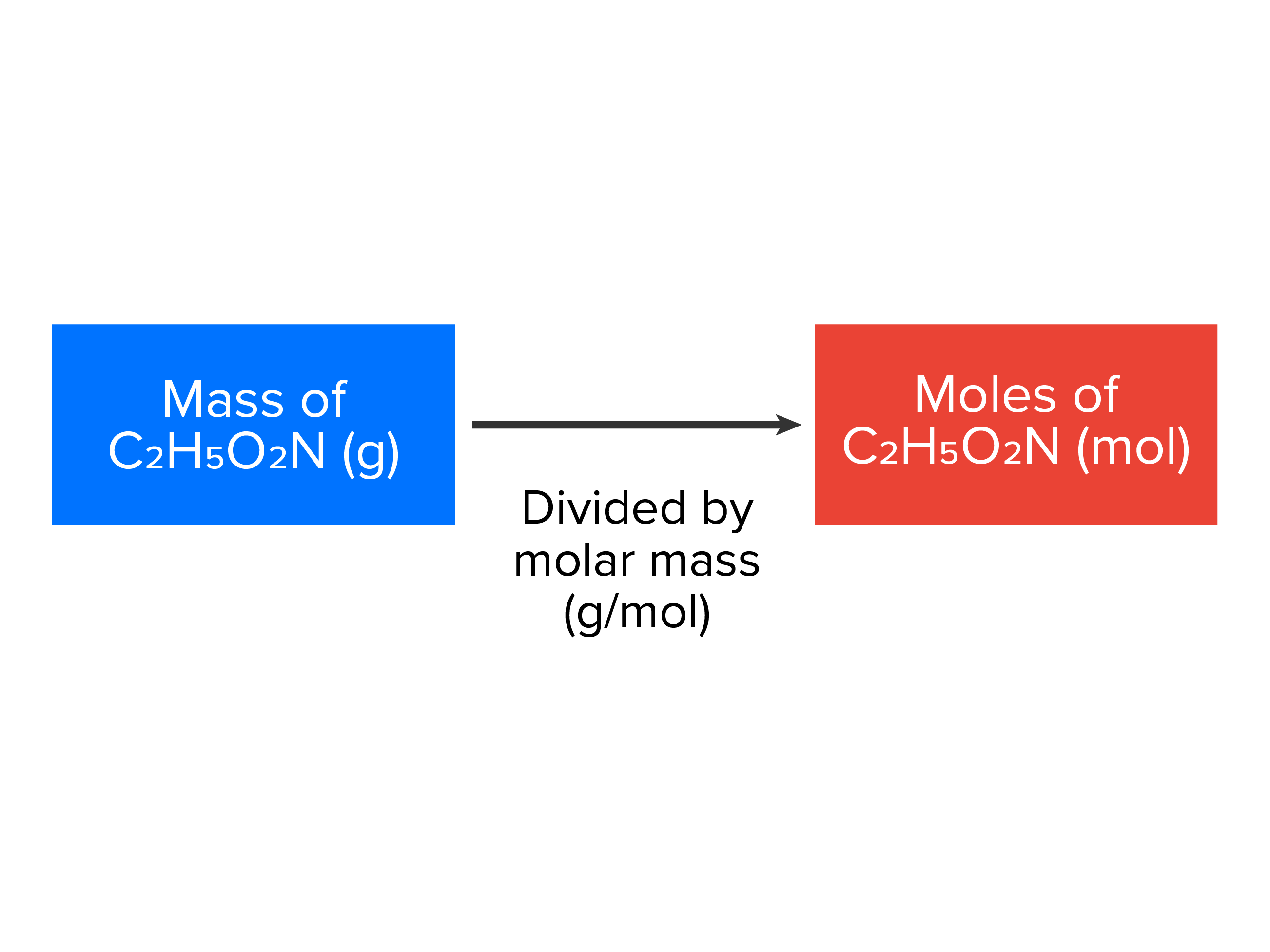
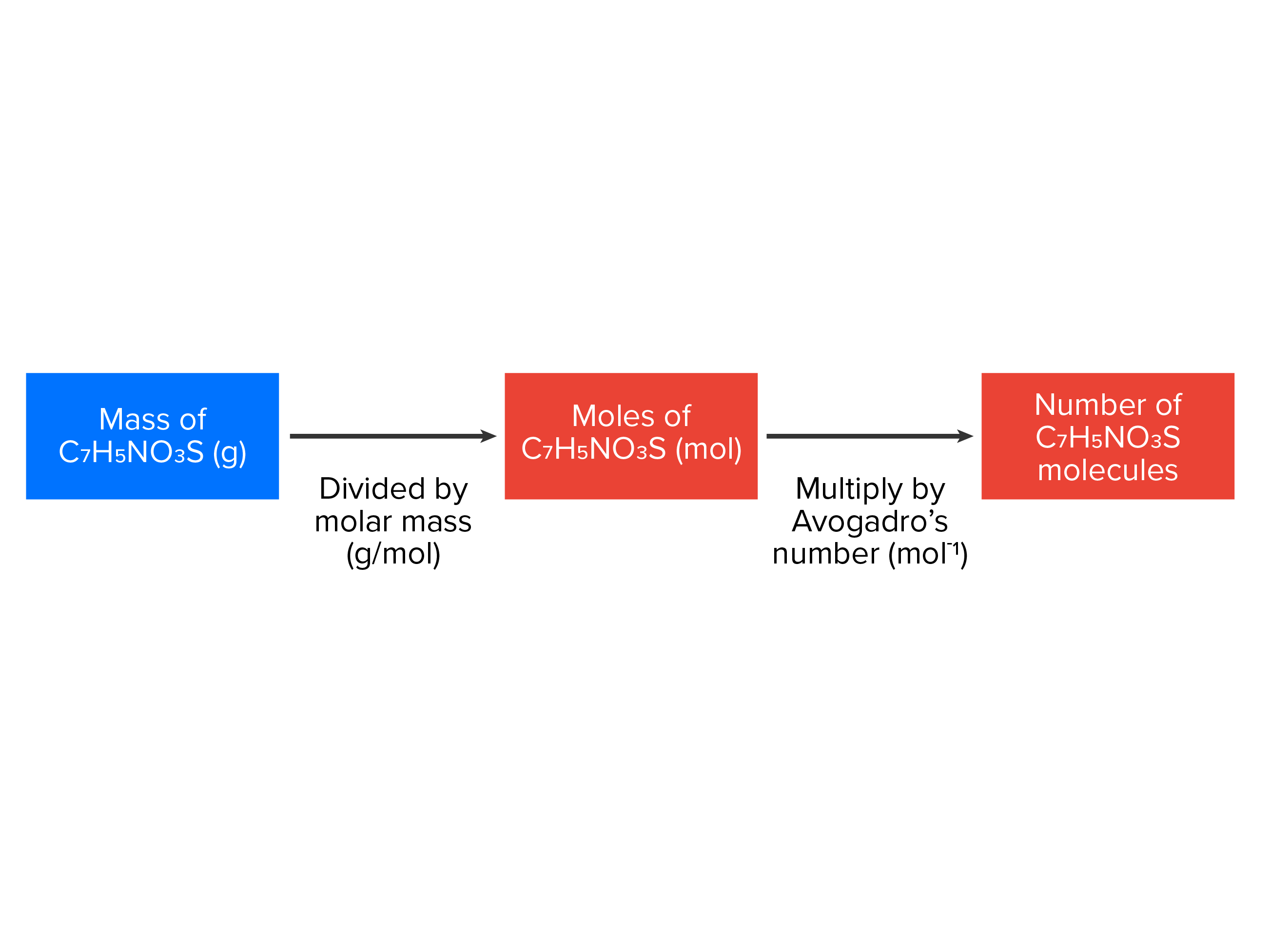
The relationships between formula mass, the mole, and Avogadro’s number can be applied to compute various quantities that describe the composition of substances and compounds. For example, if we know the mass and chemical composition of a substance, we can determine the number of moles and calculate the number of atoms or molecules in the sample. Likewise, if we know the number of moles of a substance, we can derive the number of atoms or molecules and calculate the substance’s mass. The formulas for these conversions are below.

formula to know

grams/molar mass = moles

moles x molar mass = grams

molecules (or atoms)/Avogadro’s number (6.022 x 10²³) = moles

moles x Avogadro’s number (6.022 x 10²³) = molecules (or atoms)

A good way to think about conversions is to use a concept map, which is just a visual representation of the information you need to remember. The concept maps below represent the mathematical formulas you need to know to convert between grams, moles and particles (atoms or molecules).

Formula	Concept Map
grams/molar mass = moles
moles x molar mass = grams
moles x Avogadro’s number (6.022 x 1023) = molecules (or atoms)
molecules (or atoms)/Avogadro’s number (6.022 x 1023) = moles

IN CONTEXT

While the concept of a mole might be unfamiliar to you, you do calculations similar to these all the time without any issue. If someone said they have a dozen eggs, you know right away that is 12 eggs or if someone said they have a pair of tickets to a concert, you know they have 2 tickets.

Think of moles the same way. If I tell you I have a mole of carbon, that means I have 12.01 grams of carbon or 6.022 x 10²³ atoms of carbon. So, what if I said I have 3 moles of carbon, how many grams would I have? Think of this the same way as you would with dozens. If someone said they have 3 dozen donuts, you would know they have 36 donuts (3 x 12). So, if I have 3 moles of carbon, I have 36.03 grams of carbon (3 x 12.01).

What if someone said they have 48 donuts, and you were asked how many dozens of donuts they have? In your head, you would take 48/12 = 4 dozen. So if I said you have 105 grams of carbon, how many moles do you have? You should think the same way. There are 12.01 grams in a mole, so 105/12.01 = 8.74 moles.

Below are examples of using these formulas in calculations. Make sure you can do these types of calculations.

EXAMPLE

Deriving Grams from Moles for an Element

A liter of air contains 9.2 ×10^-4 mol argon. What is the mass of Ar in a liter of air?

Solution:

Referring to the periodic table, the atomic mass of Ar is 39.95 amu, and so its molar mass is 39.95 g/mol. The mass amount of a substance may be calculated by multiplying its moles (mol) by its molar mass (g/mol):



Mass of Ar = moles of Ar x molar mass of Ar = 9.2 × 10^-4 mol Ar x 39.95 g/mol Ar = 0.037g Ar

EXAMPLE

Deriving Moles from Grams for an Element

How many moles are in 4.7 grams of potassium (K)

Solution:

Referring to the periodic table, the atomic mass of K is 39.10 amu, and so its molar mass is 39.10 g/mol. The molar amount of a substance may be calculated by dividing its mass (g) by its molar mass (g/mol) Moles of K = 4.7 g/39.10 g/mol = 0.12 moles of K

EXAMPLE

Deriving Moles from Grams for a Compound

The amino acid glycine has the molecular formula C₂H₅O₂N. How many moles of glycine molecules are contained in 28.35 g of glycine?

Solution:

Don’t get confused by the size of the molecule. It doesn't matter here. All you need to do is calculate its molar mass using the periodic table.



The molar mass of glycine is required for this calculation, and it is computed in the same fashion as its molecular mass. One mole of glycine, C₂H₅O₂N, contains 2 moles of carbon, 5 moles of hydrogen, 2 moles of oxygen, and 1 mole of nitrogen:

2 moles of carbon times the molar mass of 12.01 g/mol = 24.02 g
5 moles of hydrogen times the molar mass of 1.008 g/mol = 5.040 g
2 moles of oxygen times the molar mass of 16.00 g/mol = 32.00 g
1 moles of nitrogen times the molar mass of 14.007 g/mol = 14.007 g

Add these together to get 75.07 grams for one mol, which is the the molar mass of glycine, C₂H₅O₂N.

Moles of glycine = 28.35 g/75.07 g/mol = 0.3776 moles of glycine

EXAMPLE

Deriving Number of Atoms from Mass for an Element

How many copper atoms are in 5.00 g of copper wire?

Solution:

The number of atoms of a substance may be calculated by a two-step conversion: first calculating the moles of Cu, and then using Avogadro’s number (N_A) to convert this molar amount to number of Cu atoms:



Referring to the periodic table, the atomic mass of Cu is 63.55 amu, and so its molar mass is 63.55 g/mol.

Moles of Cu = 5.00 g/63.55 g/mol = 0.0787 moles of Cu

Atoms of Cu = 0.078 mol x 6.022 x 10²³ atoms/mol = 4.74 x 10²² atoms

EXAMPLE

Deriving the Number of Atoms and Molecules from the Mass of a Compound

A packet of an artificial sweetener contains 40.0 mg of saccharin (C₇H₅NO₃S).

Given that saccharin has a molar mass of 183.18 g/mol, how many saccharin molecules are in a 0.0400 gram sample of saccharin? How many carbon atoms are in the same sample?

Solution:

The number of molecules in a given mass of compound is computed by first deriving the number of moles, and then multiplying by Avogadro’s number:



Using the provided mass and molar mass for saccharin yields:

molecules = (0.0400 grams/183.18 g/mol) x 6.022 x 10²³ molecules/mol = 1.32 x 10²⁰ molecules of saccharin

Since there are 7 carbons in every molecule of saccharin (C₇H₅NO₃S), we multiply the molecules of saccharin by 7 to get the molecules of carbon:

1.32 x 10²⁰ molecules of saccharin x (7 molecules of C/1 molecule of saccharin) = 9.24 x 10²⁰ molecules of carbon