Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Quadratic Equations with No Real Solution

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to determine if a quadratic equation has real or non-real solutions by finding the value of the discriminant. Specifically, this lesson will cover:

Table of Contents

1. The Discriminant of the Quadratic Formula

Working with the quadratic formula is one method in determining if there are no real solutions to a quadratic equation. Recall the quadratic formula:

formula to know
Quadratic Formula
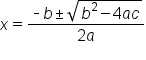
x equals fraction numerator short dash b plus-or-minus square root of b squared minus 4 a c end root over denominator 2 a end fraction

The expression that is underneath the square root is called the discriminant. Because the discriminant is underneath a square root sign, it must not have a negative value, otherwise the square root does not evaluate to a real number. This is how we can tell if a quadratic has no real solutions by using the quadratic formula.

formula to know
Discriminant
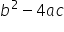
b squared minus 4 a c

The following table shows the different types of solutions when the discriminant is positive, zero, and negative.

Discriminant (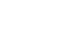bold italic b to the power of bold 2 bold minus bold 4 bold italic a bold italic c) Type of Solutions
Positive Two Real Solutions
Zero One Real Solution
Negative Two Complex Solutions

In addition, if the discriminant is a perfect square (such as 16 or 81), the quadratic equation has two rational solutions (the solutions will not contain radicals).

EXAMPLE

Find the discriminant for the quadratic equation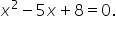 x squared minus 5 x plus 8 equals 0. Then determine if the equation has real or nonreal solutions.

First, find the discriminant:

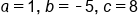
a equals 1 comma space b equals short dash 5 comma space c equals 8 Identify the values to substitute into the discriminant formula.
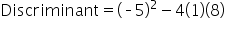
Discriminant equals open parentheses short dash 5 close parentheses squared minus 4 open parentheses 1 close parentheses open parentheses 8 close parentheses Substitute the values of a, b, and c.
Discriminant equals short dash 7 Simplify the expression.

The value of the discriminant is -7, which means the quadratic equation has no real solution.

big idea
If the value of the discriminant is equal to 0 or greater than 0, then you're going to have a real solution for your quadratic equation. If the value of the discriminant is less than 0, then you're going to have a non-real solution for your quadratic equation.

2. Negative Square Roots and the Imaginary Unit

Even though some quadratic equations may have no real solutions, we can still express their solutions mathematically. To do so, we use the imaginary number, i, in the expression for its solution. The imaginary number, i, is a non-real number that represents the square root of -1.

formula to know
Imaginary Number
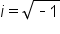
i equals square root of short dash 1 end root

The letter i is used to denote the square root of negative 1. We can rewrite the square roots of negative numbers using this letter.

EXAMPLE


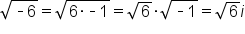
square root of short dash 6 end root equals square root of 6 times short dash 1 end root equals square root of 6 times square root of short dash 1 end root equals square root of 6 i
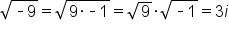
square root of short dash 9 end root equals square root of 9 times short dash 1 end root equals square root of 9 times square root of short dash 1 end root equals 3 i
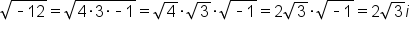
square root of short dash 12 end root equals square root of 4 times 3 times short dash 1 end root equals square root of 4 times square root of 3 times square root of short dash 1 end root equals 2 square root of 3 times square root of short dash 1 end root equals 2 square root of 3 i

term to know
Imaginary Number
A non-real number that is expressed in terms of the square root of a negative number (usually the square root of -1, represented by i ).

3. Complex Solutions to Quadratic Equations

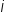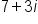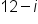If we encounter a negative value underneath the radical when using the quadratic formula, we can express the solutions to the quadratic equation using complex numbers. A complex number contains a real part and an imaginary part, such as 7 plus 3 i or 12 minus i.

EXAMPLE

Suppose we were calculating the solutions to a quadratic equation and got to this step:

x equals fraction numerator 6 plus-or-minus square root of short dash 16 end root over denominator 2 end fraction

This tells us that there are no real solutions since we cannot have a negative number in the discriminant. We can rewrite this result as complex numbers.

x equals fraction numerator 6 plus-or-minus square root of short dash 16 end root over denominator 2 end fraction Rewrite square root
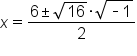
x equals fraction numerator 6 plus-or-minus square root of 16 times square root of short dash 1 end root over denominator 2 end fraction Evaluate the square root of 16 and -1
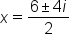
x equals fraction numerator 6 plus-or-minus 4 i over denominator 2 end fraction Create two separate solutions, one addition and one subtraction
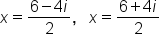
x equals fraction numerator 6 minus 4 i over denominator 2 end fraction comma space space space x equals fraction numerator 6 plus 4 i over denominator 2 end fraction Divide each term by 2
x equals 3 minus 2 i comma space space space x equals 3 plus 2 i Our solutions

In this example, the complex number 6 ± 4i was divided by 2. We can divide 6 and 4i by 2 separately to arrive at 3 ± 2i. Then, we can create two expressions, one taking the minus sign, and the other taking the plus sign, due to the ± symbol.

term to know
Complex Number
A number containing a real component and an imaginary component.

summary
If the discriminant of the quadratic formula is greater than or equal to 0, then the solutions to the quadratic equation will be real numbers. If the discriminant is less than 0, the equation has no real solution. Looking at the graph of a quadratic equation, if the parabola does not cross or intersect the x-axis, then the equation has no real solution. No real solution does not mean that there is no solution, but that the solutions are not real numbers. Negative square roots and the imaginary unit are used to find complex solutions to quadratic equations.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Terms to Know
Complex Number

A number in the form a plus b i, containing a real part, a, and an imaginary part, bi, where i is the imaginary unit, square root of short dash 1 end root.

Imaginary Number

A non-real number that is expressed in terms of the square root of a negative number (usually the square root of -1, represented by i).

Formulas to Know
Discriminant

b squared minus 4 a c

Imaginary Number

i equals square root of short dash 1 end root

Quadratic Formula

x equals fraction numerator short dash b plus-or-minus square root of b squared minus 4 a c end root over denominator 2 a end fraction

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.