Table of Contents |
The general form of a quadratic function is 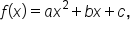 where
where 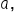 b, and c are real numbers and
b, and c are real numbers and 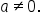
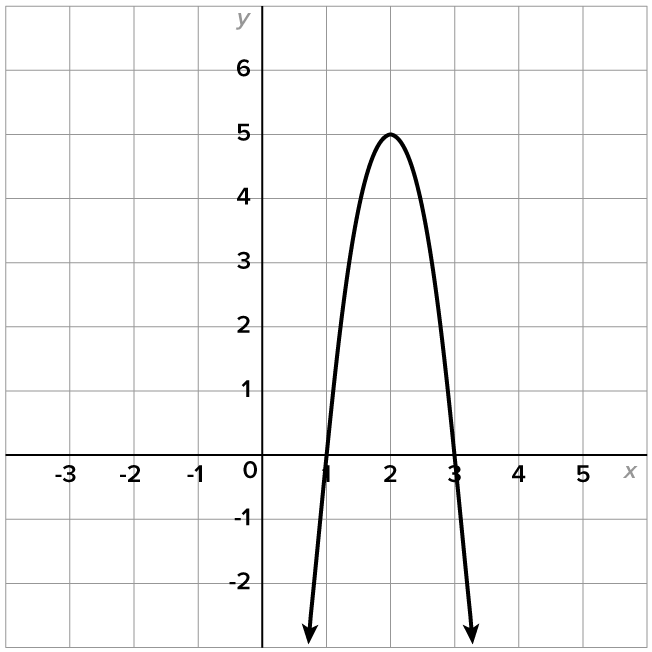
The graph of a quadratic function has a shape called a parabola. Some examples are below.

|
|
The characteristics of a parabola are shown in the graph below.
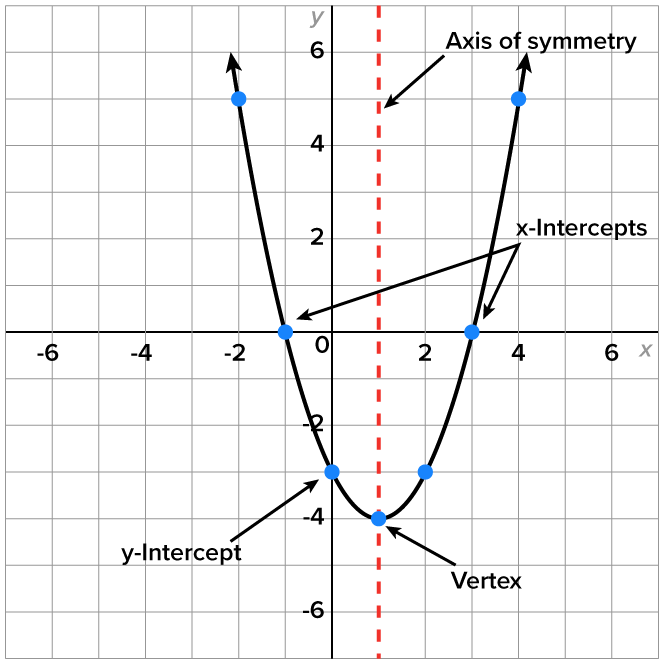
Note: parabolas can open upward or downward, as you saw earlier.
The axis of symmetry is a vertical line that passes through the vertex and divides the parabola into two equal parts.
Every parabola has a y-intercept.
Parabolas can have zero, one, or two x-intercepts.
Here is an example problem where we can pull these ideas together.
EXAMPLE
Identify the axis of symmetry, vertex, x-intercepts, and the y-intercept.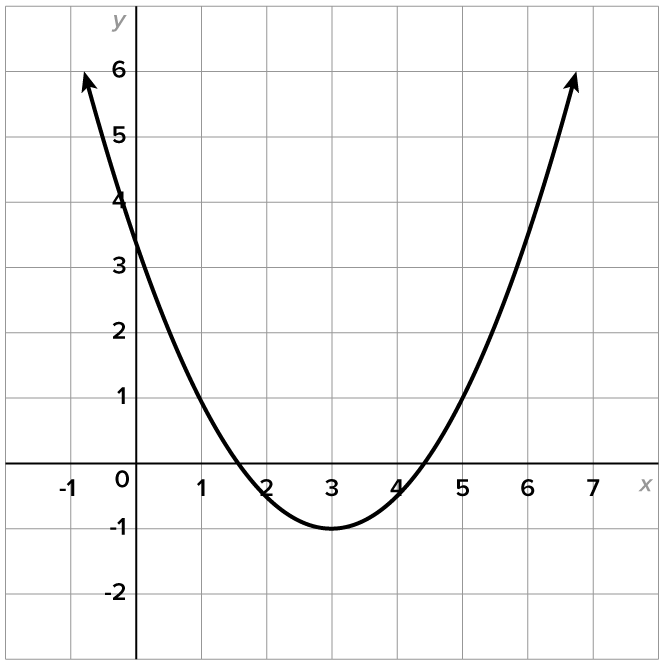

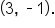
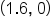 and
and 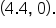
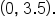
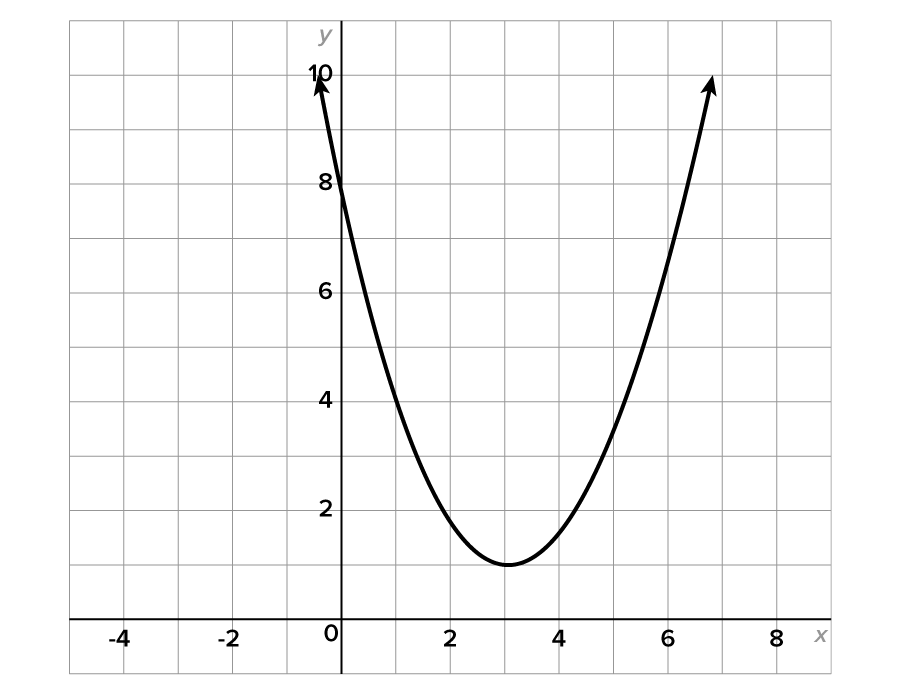
In the next section, we will use the equation to find its vertex.
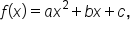 where
where 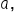 b, and c are real numbers and
b, and c are real numbers and 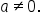
The most basic quadratic function is 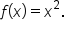
Note that its vertex is at 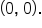
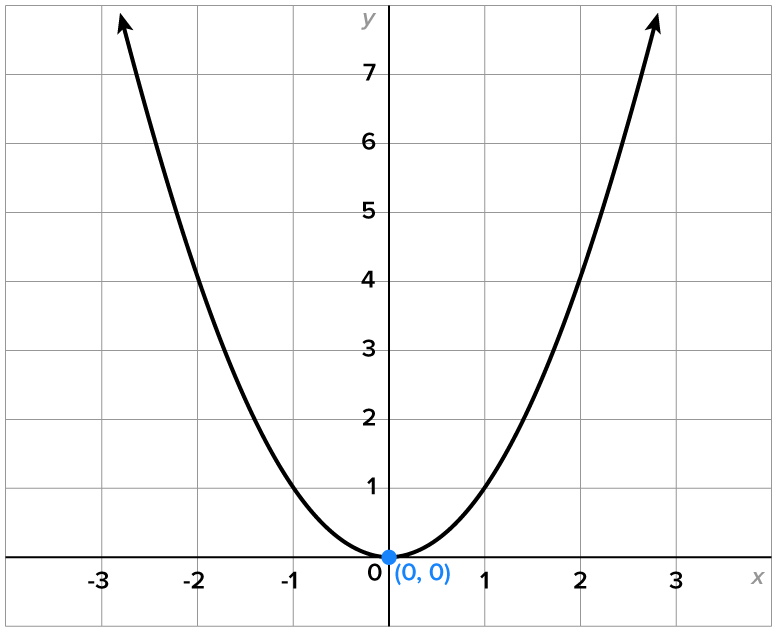
Now, consider the graph of 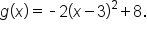
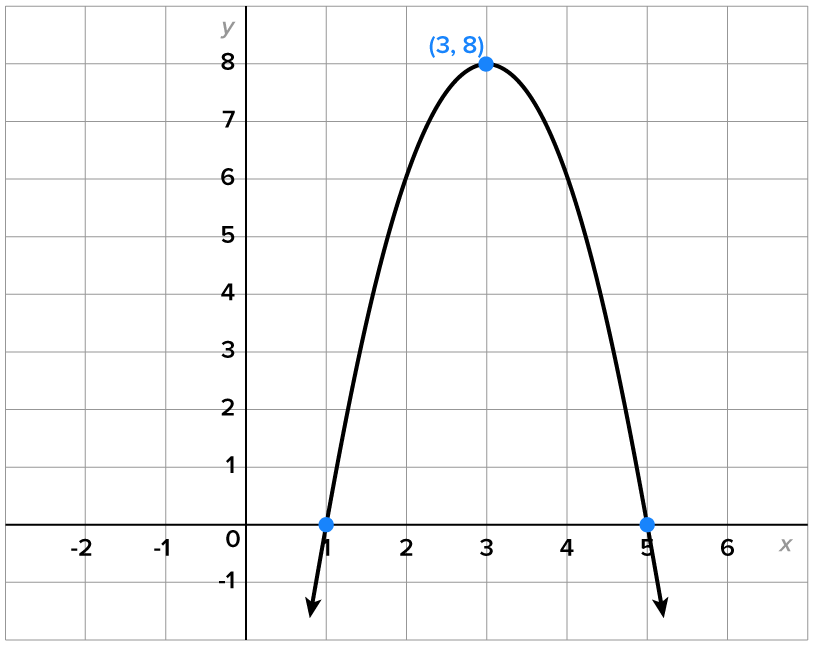
From earlier in the course, we know that the graph of 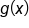 is obtained by applying a series of transformations to the graph of
is obtained by applying a series of transformations to the graph of 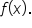
Namely,  is shifted to the right 3 units, reflected over the x-axis, vertically stretched, and shifted up 8 units.
is shifted to the right 3 units, reflected over the x-axis, vertically stretched, and shifted up 8 units.
Note that its vertex is located at the point 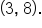
The standard form of a quadratic function is 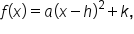 where
where 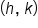 is the vertex.
is the vertex.
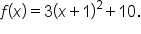
While the standard form is useful for finding the vertex, how would we find the vertex of a parabola whose equation is in the form 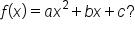
That is, can we find expressions for h and k in terms of 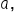 b, and c?
b, and c?
Suppose the two forms represent the same parabola. Then, we know they are equal.
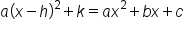
|
Set the two forms equal to each other. |
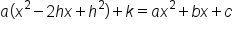
|
Expand 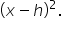
|
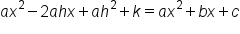
|
Distribute. |
Since these are two functions of x, the coefficients of each term, 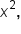 x, and constant, need to be equal to each other in order for the equation to hold:
x, and constant, need to be equal to each other in order for the equation to hold:
| Term | Left-Hand Side Coefficient | Right-Hand Side Coefficient |
|---|---|---|
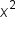
|

|

|
| x |
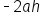
|
b |
| Constant (No x’s) |
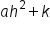
|
c |
Note that the coefficients of 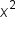 are the same in both forms.
are the same in both forms.
The most important result is the x term: since the coefficients are to be the same, we have 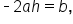 which means that
which means that 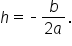
Equating the constant terms, we have 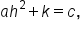 which means
which means 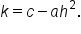 Substituting
Substituting 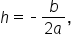 this becomes
this becomes 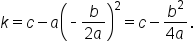 This is a more complicated formula, and is unnecessary to remember.
This is a more complicated formula, and is unnecessary to remember.
This leads us to a formula for the vertex when the quadratic has the form 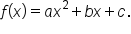
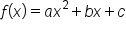 , where
, where 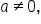 its vertex is located at the point
its vertex is located at the point 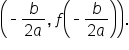
EXAMPLE
Find the coordinates of the vertex of the parabola whose equation is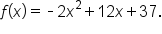
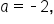
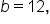 and
and 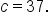
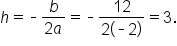
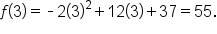
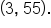
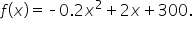
Putting some aspects of the equation of a parabola together, the vertex can be used to determine the minimum or maximum value of a quadratic function.
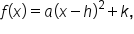 where
where 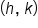 is the vertex.
is the vertex.Consider the general form of a quadratic function, 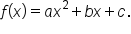
In the last section, we saw that the sign of  determines the direction the parabola opens.
determines the direction the parabola opens.
If 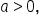 the parabola opens upward. The vertex is the lowest point on the parabola.
the parabola opens upward. The vertex is the lowest point on the parabola.
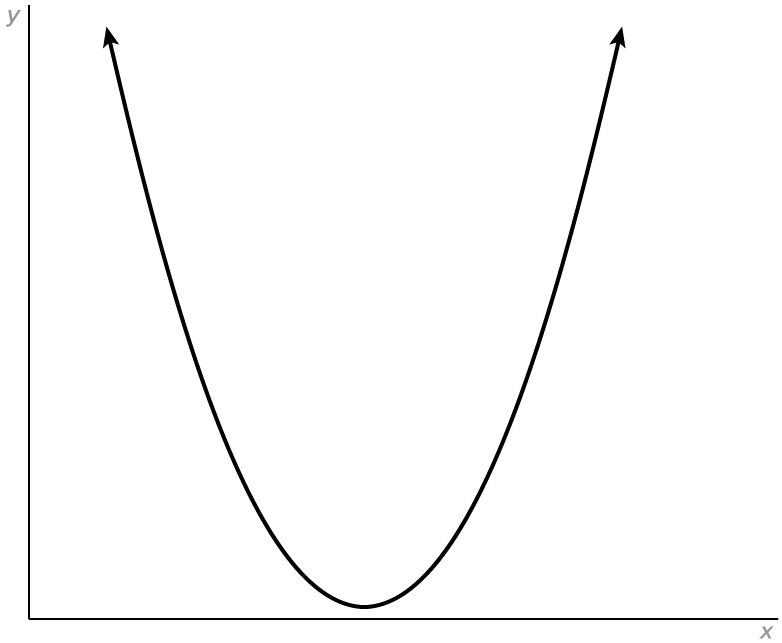
If 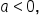 the parabola opens downward. The vertex is the highest point on the parabola.
the parabola opens downward. The vertex is the highest point on the parabola.
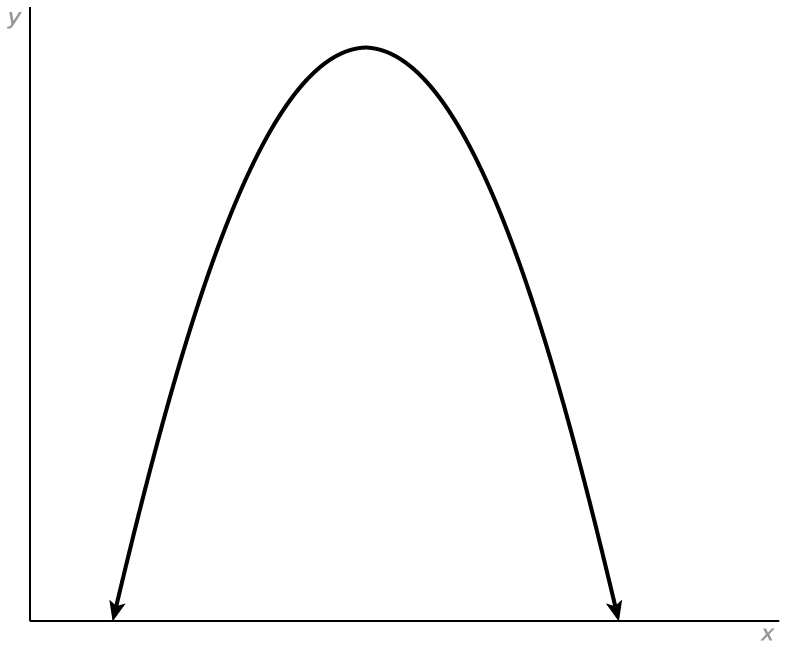
This leads to the following generalization.
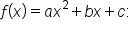
 the vertex is the lowest point on the graph of
the vertex is the lowest point on the graph of  The minimum value of
The minimum value of  is the y-coordinate of the vertex.
is the y-coordinate of the vertex. 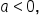 the vertex is the highest point on the graph of
the vertex is the highest point on the graph of 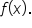 The maximum value of
The maximum value of  is the y-coordinate of the vertex.
is the y-coordinate of the vertex.EXAMPLE
Consider the equation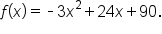 Find its vertex and determine whether the minimum or maximum value of f occurs at the vertex.
Find its vertex and determine whether the minimum or maximum value of f occurs at the vertex.
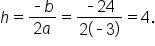
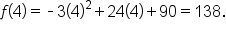 Therefore, the vertex is located at the point
Therefore, the vertex is located at the point 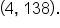
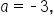 which is negative, this means that the maximum value of f occurs at the vertex, and is equal to 138.
which is negative, this means that the maximum value of f occurs at the vertex, and is equal to 138.
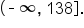
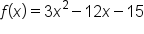 are discussed.
are discussed.
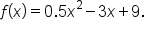
In applications, if a quantity is modeled by a quadratic function, it is possible to determine the minimum or maximum value of that quantity by examining its equation (no need to use a graph).
EXAMPLE
When an object is thrown from the top of a 200-foot tall building, its height after t seconds is modeled by the function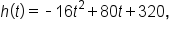 where h is measured in feet.
where h is measured in feet.
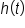 is a quadratic function with
is a quadratic function with 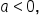 the vertex can be used to determine the maximum height of the object.
the vertex can be used to determine the maximum height of the object.
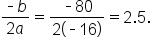
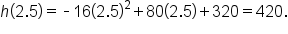
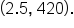
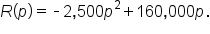
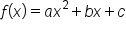 ) by using the formula for the vertex of a parabola. If the equation of the quadratic is known, then a formula can be used to determine the coordinates of the vertex, which can then be used to determine the maximum or minimum values of a quadratic function, whose applications include finding the maximum height of an object thrown and evaluating a newspaper's subscription price/revenue model.
) by using the formula for the vertex of a parabola. If the equation of the quadratic is known, then a formula can be used to determine the coordinates of the vertex, which can then be used to determine the maximum or minimum values of a quadratic function, whose applications include finding the maximum height of an object thrown and evaluating a newspaper's subscription price/revenue model.
SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS