Table of Contents |
We have learned how to calculate the probability of something happening, even the probability of two things happening. But how do you calculate the probability that something will not happen?
This brings up a simple property of probability. The probability of something happening is expressed as a number between 0 and 1. The range between 0 and 1 represents all possibilities. Thus, the probability of an event not happening is 1 minus the probability that it will happen. This is also called the inverse.
For example, suppose you are playing a board game and want to determine the probability that you will not roll a 12. We saw previously that rolling a 12 on two normal dice is 1/36, so it follows that the probability of not rolling a 12 is 35/36, or 97.2%.
We can now return to the dilemma we faced earlier, of calculating the probability of winning a game of Three Card Monte at least once on two tries. In this case, we win if either we pick the Queen the first time or the second time.
How do we calculate this probability? We can’t multiply probabilities, as we did earlier, because we aren’t worried about drawing a Queen both times. We also can’t simply add the probabilities together, or we’d get to 100% on three tries, and while we’re likely to win, it’s not 100% certain.
In fact, there is an easy—but not so obvious—solution to this problem. We calculate the probability of not getting a Queen on either draw, and then subtract that answer from 1. Remember that the probability of all possible outcomes must sum to 1, so P(Queen) + P(not Queen) = 1.
Again, we’ll assume the dealer is playing a straight game (which is a dangerous assumption in real life!). The probability of losing the first game is 2/3, or .667. The probability of losing the second game is the same. Using the formula we learned earlier for two events both occurring, we multiple .667 by .667 and get .445. Remember, this is the probability of not winning either game, but we can calculate the probability of winning at least once by subtracting this figure from 1, and get .555. We have a 55.5% chance of winning. We can only arrive at this by combining two of the formulas we’ve learned, the probability of an event not happening and the probability of multiple events occurring.
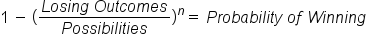
Let’s look at another complex problem: winning the lottery. You know the probability of winning is low, but how do you calculate the odds?
Let’s say we have a simple lottery where we pick three numbers between 1 and 30. You have to get all three numbers right to win the jackpot. The balls are drawn from one machine without replacement, meaning that these are dependent events where no number can be drawn twice.
We can use the formula for multiple events to calculate the probability of getting the five numbers right, keeping in mind that subsequent draws will change the total distribution of possibilities:
But wait! We calculated the probability for getting each number right, but forgot a crucial detail. We do not have to get the numbers in the right order. Say we pick the numbers 7, 11, and 22. Our calculation above shows the probability of the numbers being drawn in that order. But they could be drawn in the order 11, 22, and 7. Or 22, 7, and 11. We win in any of these combinations. How do we calculate the real probability?
Imagine yourself listening as they draw the numbers. On the first draw, any of the three numbers out of the 30 balls will keep you in the game. On the second draw, there will be two balls out of 29 that will keep you in the game. (We are only calculating the chances of winning; if the first ball is a miss, you are already out of the game.) On the last draw, there are 28 balls and only one with your lucky number. So, we would calculate it like this:
EXAMPLE
The multistate Powerball requires the player to pick five numbers between 1 and 69 and one more number (the eponymous powerball) between 1 and 26, which is independent of the first five. Imagine, even if you get the first five numbers right (which is about one in 11 million), you still have a 25 in 26 chance of losing! Fortunately for Powerball players, there is still a prize for matching all but the powerball, but it is measured in thousands instead of in millions.The birthday problem is a classic problem that measures the probability of two people having the same birthday. Conceptually, it shows how coincidences can be more common or likely than we first think.
The probability that two people have the same birthday is 1 in 365 (or 4 in 1461, if you consider leap year, February 29, but we will be ignoring leap year) for .0027, or 0.27%. That is about one fourth of one percent. Note that the reason this is only 1/365 and not 2/365 is because the 1 here represents a single event of matching, not the number of birthdays.
Now, what are the chances that in a group of three people, any two will have the same birthday? This might be perplexing until you remember the trick of calculating the probability of something not happening: calculate the probability that it happens, then subtract it from 1. We treat each person having a unique birthday (not one they share with anyone else in the group) as an independent event. So, for three people, we can see the second person has a 364/365 (99.7%) chance of having a unique birthday, and the third has a 363/365 (99.4%) chance of having a unique birthday. The chances of both of those occurring is 99.1%. Subtracted from 1, we have a 0.9% chance of two of those three people having the same birthday.
Obviously, the probability will continue to drop as we add people to the group. The question is, how many people must be in the party before the probability of two having the same birthday is better than .5? Better than .75?
The birthday problem is about coincidences. Conceptually, you can use the same reasoning for answering the question, “What is the chance?” when any coincidence occurs. Perhaps you meet a stranger with the same last name, or find a book at a used bookstore with the inscription “Property of XYZ,” and you happen to know the person XYZ. In any of these cases, the probability seems much more remote if you focus on the one outcome.
It is unlikely that two people you know will both have the same birthday, but quite likely that any two random colleagues will have the same birthday. It is unlikely that the person in the next seat on the next flight will have the same last name as you, but perhaps likely (depending on your name!) that over a lifetime of trips and encountering strangers, you will meet one or two with your name. The chances of finding a book at Half Price Books this afternoon that used to belong to Xaviar are indeed long, but if you frequent used bookstores and have friends who like the same books, the chances of eventually experiencing a coincidence like that are not so long. The birthday problem (and coincidences in general) compel us to remember the big picture and ask ourselves, “What is the chance of this never happening?”, to have more context. This doesn’t mean we can’t enjoy a coincidence and tweet about it!
Source: THIS CONTENT HAS BEEN ADAPTED FROM Introduction to Logic and Critical Thinking.
