Probability of a Dependent Event

1. Determining Probability of Dependent Events

As you have learned in previous lessons, probability is the likelihood of an event occurring. In our last lesson, we learned how to mathematically determine the probability of two independent events by multiplying together two events that have no effect on the outcome of the second event. In this lesson, we will learn how to determine the probability of two events that do affect each other. For example, running and rolling your ankle or fishing and keeping the fish you land.

Like with determining the probability of independent events, you will multiply the probability of each of the events occurring. However, the difference is: what occurs with the first event will affect the second. For example, when fishing, if you keep the fish that you catch and do not throw them back into the pond, there is now one less type of that fish that you can catch.

EXAMPLE

You are fishing in a stocked pond. You know that the pond contains 5 bluegill, 10 perch, and 8 bass. What is the probability that you will catch a bluegill to eat and then a bass fish?

To solve this problem, we must first find the probability of the first event and then the probability of the second event. The first event is catching a bluegill fish out of the pond. This process is similar to what we have done in the previous section. The numerator is the number of a favorable outcome. There are 5 bluegill fish in the pond. This is our numerator. If we add all the fish in the pond, there are fish. So, the probability of the first event is .

What is different between the probability of an independent and dependent event is that to find the probability of the second event, you now have to take into consideration what happened in the first event. For the first event here, one bluegill fish is taken out of the pond. So, for the second event, there are no longer 23 fish in the pond. There are only 22 fish in the pond.

Now, to find the probability of the second event, we take the number of favorable outcomes, or the number of bass fish in the pond. There are 8 bass fish in the pond. The first event did not affect the number of bass fish still in the pond. But, there are only 22 total fish remaining in the pond. So, the probability of catching a bass fish after catching a bluegill is .

To find the probability of both events happening together, we multiply the two probabilities together:


Multiply and simplify the two fractions.



The probability of catching a bluegill first to eat and then a bass is .

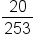EXAMPLE

You have a bag of marbles containing 2 red, 4 blue, 5 green, 1 yellow, and 3 white. What is the probability of pulling out 1 red marble, and then 1 yellow marble without putting either marble back into the bag?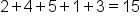

The probability of the first event, pulling out a red marble, is 2 out of 15, since there are a total of marbles. For the second draw, we have to consider the results of the first draw. The first marble was red, which doesn't affect the number of yellow marbles remaining. So we still have one marble left in the bag. However, since a marble was already drawn and not put back, we only have 14 marbles to choose from, rather than 15. So the probability of drawing a yellow marble on the second draw is .

To find the probability of both events happening together, we multiply the two probabilities together:


Multiply and simplify the two fractions.

try it

You are second in line to get ice cream at a high school game. The first customer randomly chooses one serving of ice cream from the choices of 5 servings of vanilla, 6 servings of chocolate, and 3 servings of strawberry.

What is the probability that the person in front of you randomly picks vanilla and then you randomly pick strawberry ice cream?

Multiply and simplify the two fractions.



The fraction cannot be simplified, so no additional steps are needed.

try it

You are getting dressed in the dark and need two socks. Unfortunately, you never fold your socks and you cannot see what you’re pulling out. Your sock drawer has 20 single socks, that consist of 4 tan, 6 white, 8 black, and 2 T-Rex socks.

What is the likelihood of you pulling out 2 black socks for work?

Multiply and simplify the two fractions.