Probability Distribution

1. Discrete Probability

This spinner has eight equally sized sectors. If you spin the spinner, there are three sectors marked with a 1, one marked with a 2, two marked with a 3, and another two marked with a 4. All the sectors are equally likely, but not every outcome is equally likely.

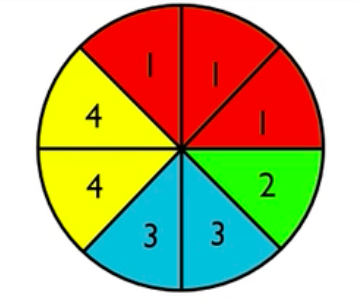
A probability distribution can be set up for the spinner. The probability distribution is a lot like a frequency distribution, except it will be set up as probabilities instead of frequencies. All the outcomes that could happen from the spinner will be listed.

Next, instead of how often each number comes up in terms of frequency, we're going to list how often they come up in terms of probability. Three eighths of the time, you'll get a 1. One eighth of the time, you'll get a 2. Two eighths of the time, you'll get a 3, and two eighths of the time, you'll get a 4.

Number	1	2	3	4
Probability

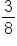
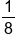
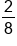
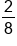
Two things should be noticed with this probability distribution:

1. Each individual probability must be between 0 and 1.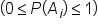

Every probability—the three eighths, one eighth, two eighths, etc.—is a number between 0 and 1. Any probability in a probability distribution has to be between 0 and 1, inclusive.

2. The sum of all probabilities must be 1.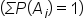

The sum of all the probabilities in the probability distribution is 1. It makes sense—with a probability of 1, it's certain that you will get a 1, 2, 3 or 4 on this spinner.

Number	1	2	3	4
Probability

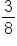
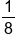
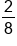
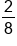
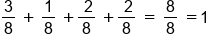
This type of probability is called a discrete probability distribution, which means there are only so many outcomes.

try it

Consider two flips of a coin. Here are your four possibilities.

Possible Outcomes When Flipping Two Coins
Heads - Heads	Heads - Tails	Tails - Heads	Tails - Tails

Next, create a probability distribution for the number of tails. You should have come up with something like this:

Probability Distribution When Flipping Two Coins
Tails	0	1	2
Probability

The probability that you get zero tails is a fourth, a half probability of getting one, and one fourth probability of two tails on the two flips. Notice once again, each of those probabilities is a number between 0 and 1. In addition, one fourth plus one half plus one fourth adds up to 1.

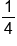
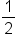
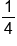
The coin and spinner scenarios are both discrete probability distributions because there are only so many outcomes.

terms to know

Probability Distribution

A description of the possible outcomes and their probability of occurring.

Discrete Probability Distribution

A probability distribution with only so many values. The probabilities can be listed in a table alongside the potential outcomes.

2. Continuous Probability

There are also probability distributions that are continuous probability distributions in which the probability is related by some mathematical function. For example, the normal distribution is a probability distribution.

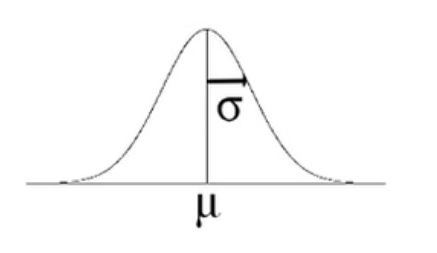
In this case, the area under the curve should equal one, and the graph should lie entirely above or on the x-axis. That's how those two rules apply to continuous distributions. With a continuous distribution, an outcome can be anything within this range on the x-axis.

term to know

Continuous Probability Distribution

A probability distribution where probabilities are related by a mathematical function, and the outcomes can take any value within a given range.

3. Countably Infinite Outcomes

It is important to note that some distributions have what we call countably infinite outcomes.

EXAMPLE

Suppose you are interested in the number of rolls it takes to obtain a 6 on your die. If you rolled a 6 on your first roll, that would be a 1 because it took you one roll. If you rolled it on your second trial after missing on the first trial, then it would be a 2.

However, suppose you rolled 4, 2, 3, 2, 3, 4, 5, 2, and just kept on going here; hypothetically, this could go on forever. There are infinitely many outcomes here, or infinitely many rolls that it hypothetically could take to obtain a 6. This is what we would call countably infinite outcomes.

These are considered discrete because, for instance, it can't take you one and a half rolls to obtain a 6. It has to take an integer value, like a 1 or 2 or 3. Since it can only contain these particular values as outcomes—the integers—it is discrete instead of continuous.